Принятие решений в условиях неопределенности

Отличительная особенность игры с природой состоит в том, что в ней сознательно действует только один из участников, в большинстве случаев называемый игроком А. Игрок В (природа) сознательно против игрока А не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные «ходы» партнер по игре.

К числу классических критериев, которые используются при принятии решений в играх с природой, можно отнести критерии максимакса, Вальда(максимина), Сэвиджа (минимакса), Гурвица.

Критерий максимакса. Позволяет определить стратегию, максимизирующую максимальные выплаты для каждого состояния природы. Это критерий крайнего оптимизма.

К = ,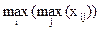

где х_ij – элемент матрицы выплат ||x_ij|| (i – номер строки, j – номер столбца).

Запись вида 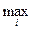означает поиск максимума перебором строк, а запись вида – поиск максимума 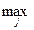перебором столбцов.

По местоположению выбранного максимального элемента определяется, например, i-й вариант приня­тия решения.

Максиминный критерий Вальда называют критерием крайнего пессимизма (консервативного игрока), т. к. при его использовании предполагается, что от любого решения надо ожидать худших последствий и поэтому надо выбрать такое решение, при котором худший из результатов будет относительно лучше других:

К = .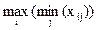

Максимин считается фундаментальным критерием. К нему надо прибегать в случаях, когда ошибки в выборе стратегии поведения могут привести к катастрофическим последствиям, а также когда решение можно принять только один-единственный раз и в последующем его изменить уже не удастся.

Критерий минимаксного риска Сэвиджа – ориентирован не столько на минимизацию потерь, сколько на минимизацию сожалений по поводу упущенной прибыли

Выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не матрицей выплат, а матрицей рисков R=||r_ij||.

При использовании критерия Сэвиджа обеспечивается наименьшее значение максимальной величины риска:

К =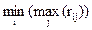

Риск r_ij определяется выражением: r_ij = β_j – x_ij, где β_j - максимально возможная выплата игрока при состоянии природы S_j (или стратегии противника с номером j):

β_j =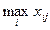

Для выбора стратегии по критерию Сэвиджа сначала находим лучшие результаты каждого отдельного столбца:

.

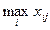Затем определяем отклонения от лучших результатов в пределах каждого отдельного столбца, т. е.

.

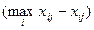Получаем матрицу отклонений или матрицу сожалений. Для каждой строки матрицы сожалений находим наибольшую величину

.

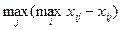Выбираем то решение, при котором максимальное сожаление будет меньше других максимальных сожалений:

К = .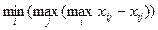

Критерий пессимизма-оптимизма Гурвица. Это суммарная комбинация стратегии оптимиста и стратегии пес­симиста. Игрок выбирает для себя, на сколько рисковать или страхо­вать в игре. Предпочтение он реализует через назначение коэффициен­та пессимизма ρ, который может принимать значения от 0 до 1.

К = ,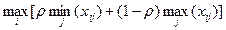

Величина параметра ρ зависит от того, как игрок оценивает ситуацию. Если он подходит к ней оптимистически, то величина ρ должна быть меньше 0,5. при пессимистической оценке ситуации игрок должен взять ρ больше 0,5. Так как параметр ρ берется довольно произвольно, то и выбор с помощью критерия Гурвица не свободен от субъективизма.

При ρ =0 критерий Гурвица совпадает с максимаксным критерием, а при ρ = 1 - с критерием Вальда.

Лекция 2