Принятие решений в условиях риска
Чтобы отобразить все возможные альтернативы принимаемого решения, имеющиеся у ЛПР, исходные данные можно представить или в виде таблицы решений, или дерева решений.
Самым простым способом подачи информации о ситуации риска является таблица решений. Возможны 2 способа использования таблицы решения при принятии решений в условиях риска: таблица выплат и таблица риска.
Таблица выплат (таблица эффективности) может быть представлена в следующем виде:
| Альтернативы (Аi) | Состояние среды (Sj) и их вероятности (рj) | |||
| S1(р1) | S2(р2) | …….. | Sn (рn) | |
| А1 | x11 | x12 | …….. | x1n |
| А2 | x21 | x22 | …….. | x2n |
| …….. | …….. | …….. | …….. | …….. |
| Аm | xm1 | xm2 | …….. | xmn |
Таблицу можно свернуть в матрицу выплат (матрицу эффективности, платежную матрицу) Х = ||xij||, где i – номер строки матрицы выплат, т. е. варианта решений (альтернативы), j – номер столбца матрицы, т. е. состояние природы.
Наличие выплат, являющихся показателями эффективности при различных состояниях среды, позволяет определить потери в результате принятия неоптимальных решений – в случае, когда ожидаемое состояние среды не наступило. Для обозначения потерь вводится специальный показатель, который называется риском. Он демонстрирует, насколько выгодна применяемая нами альтернатива при конкретном состоянии среды с учетом степени ее неопределенности. Величина риска – это размер платы за отсутствие информации о состоянии среды.
Используя показатель риска, расчет которого осуществляется на основании таблицы (матрицы) выплат, можно построить таблицу (матрицу) риска R =||rij|| или таблицу (матрицу) упущенных возможностей.
Риском rij при выборе альтернативы Аi и при состоянии среды Sj называют разность между выплатой, которую можно получить, зная, что состояние среды будет Sj и выплатой, которая будет получена при отсутствии такой информации. То есть риск rij – это разность между максимальной выплатой и выплатой по конкретной альтернативе при данном состоянии среды:
rij = βj – xij,
где βj = 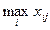 при заданном j. Например, для матрицы выплат
при заданном j. Например, для матрицы выплат
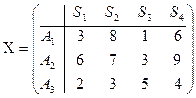
β1 = 6, β2 = 8, β3 = 5, β4 = 9.
Согласно введенным определениям rij и βj получаем матрицу рисков
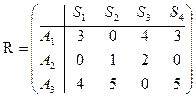
Независимо от таблицы решений требуется выбрать такую альтернативу, которая была бы наиболее выгодной по сравнению с другими.
Для выбора оптимального решения в условиях риска применяются следующие критерии:
1) при использовании таблицы выплат: максимум математического ожидания выплат(средней ожидаемой выплаты) и критерий Лапласа;
2) при использовании таблицы риска – минимум ожидаемого среднего риска.
Критерий максимума математического ожидания выплат. Для матрицы выплат X = ||xij|| оптимальной будет та альтернатива А*, которая обеспечивает максимум средней ожидаемой выплаты (СОВ), т.е. удовлетворяет условию:
А* = 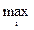 М (xi)=
М (xi)= 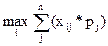 ,
,
где М (xi) – математическое ожидание для i строки;
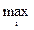 - приказ найти максимум перебором строк;
- приказ найти максимум перебором строк;
xij – выплата, которую можно получить при выборе i-той альтернативы и при j-том состоянии среды;
pj - вероятность j состояния среды;
∑(xij *pj) – средняя ожидаемая выплата.
Решение, принятие на основе критерия максимум математического ожидания выплат, может быть уточнено за счет привлечения дополнительной информации в форме расчета среднеквадратического отклонения как показателя риска.
Среднеквадратическое отклонение определяется по формуле
σi = 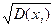
где 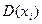 - дисперсия
- дисперсия
Дисперсия определяется по формуле:
D(хi) =σ2 = 
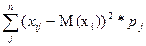 ,
,
Риск решения тем выше, чем выше значение среднеквадратического отклонения.
Окончательный выбор решений зависит от склонности ЛПР к риску.
Критерий Лапласа. Этот критерий используется, если ни одно из состояний среды нельзя назвать более вероятным, чем другие, т. е., если все они являются приблизительно равновероятными. Оптимальной является та альтернатива, которой соответствует наибольшая сумма выплат, т.е.
А* = 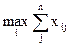
Если критерии математического ожидания и Лапласа указывают на одну и ту же альтернативу, то это является лишним подтверждением ее оптимальности. Если же критерии указывают на разные альтернативы, то предпочтение надо отдать той из них, на которую указывает критерий максимума математического ожидания. Именно этот критерий является основным.
Критерий минимум ожидаемого среднего риска. Для матрицы риска R =||rij|| лучшей будет та альтернатива, которая обеспечивает минимальный средний риск:
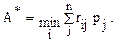
Все рассмотренные выше критерии оправдывают себя только в условиях, когда принимается не одно единственное решение, а целая серия решений. Для выработки единичных решений они не пригодны.
Многие решения, принимаемые в условиях риска, требуют анализа последовательности решений и состояний среды, когда одна совокупность стратегий ЛПР и состояний среды порождает другое состояние подобного типа. Если имеют место два (или более) последовательных множества решений, при чем последующие основываются на результатах предыдущих, и/или два (или более) множества состояний среды используется такой метод принятия решений как дерево решений.
Дерево решений – это графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выплат для любых комбинаций альтернатив и состояний среды. К нему прибегают тогда, когда решения принимаются поэтапно или когда с переходом от одного варианта решения к другому меняются вероятности. Дерево решений создается при движении слева направо, а анализируется в обратном направлении. Поэтому этот анализ называют обратным.
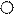 При создании дерева пункты принятия решений обозначаются квадратами (□), а узлы возникающих неопределенностей – кружками ( )
При создании дерева пункты принятия решений обозначаются квадратами (□), а узлы возникающих неопределенностей – кружками ( )
Для каждого разветвления неопределенности рассчитывается вероятность, а в конце каждой финальной ветви указывается ожидаемая выплата. При обратном анализе для каждого узла неопределенности рассчитывается математическое ожидание выплаты. Для каждого пункта принятия решения выплата максимизируется. Лучшее решение выбирается по максимуму выплат.
Схематично дерево решений представлено на рис 2
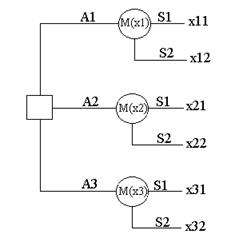
Рис. 2 Дерево решений
Дата добавления: 2015-02-19; просмотров: 1452;
