Теплопередача через плоскую и цилиндрическую стенки
В зависимости от формы и размеров теплопередающей стенки выраже-
ния для вычисления коэффициента теплопередачи имеют разный вид.
Рассмотрим лишь плоскую и цилиндрическую стенки.
Плоская стенка.При стационарнойтеплопередаче через плоскую однородную стенку (рис. 9.1) толщиной δ и коэффициентом теплопроводности λ. плотность теплового потока от первого теплоносителя к стенке, через стенку и от стенки ко второму теплоносителю одинакова:
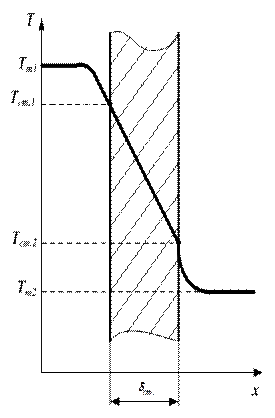 Рис. 9.1
Рис. 9.1
| 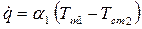 ; ;
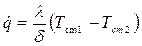 ; ;
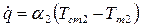 .
Отсюда выразим температурные напоры: .
Отсюда выразим температурные напоры:
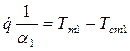 ; ;
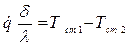 ; ;
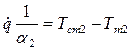 .
Просуммировав левые и правые части полученных равенств, получим: .
Просуммировав левые и правые части полученных равенств, получим:
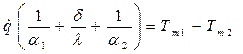 ,
или ,
или
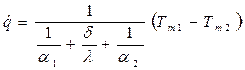 . .
|
Сомножитель у разности температур и есть коэффициент теплопередачи для плоской однослойной стенки:
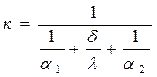 . (9.2)
. (9.2)
В итоге плотность теплового потока при теплопередаче через стенку
q = к ( Тm1 – Tm2 ). (9.3)
Величина, обратная коэффициенту теплопередачи, называется п о л-
н ы м т е р м и ч е с к и м с о п р о т и в л е н и е м т е п л о п е р е д а ч и. Для плоской однородной стенки полное термическое сопротивление записывается как
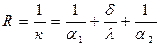 . . (9.4)
. . (9.4)
Для плоской стенки, состоящей из п неоднородных слоев, полное термическое сопротивление будет иметь вид:
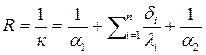 . (9.5)
. (9.5)
Цилиндрическая стенка.Получим выражение коэффициента теплопередачи для однородной цилиндрической стенки с внутренним диаметром d1 и наружным d2. Коэффициент теплопроводности материала стенки λ примем независимым от температуры. При установившемся тепловом режиме и известных Tm1, Tm2, α1 и α2 тепловой поток, отнесенный к длине стенки, запишется как
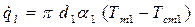 ;
;
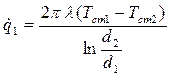 ;
;
. 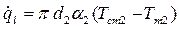 .
.
Решая полученные уравнения относительно разности температур, а затем, складывая, получим:
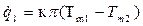 , (9.6)
, (9.6)
где
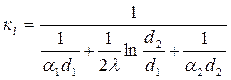 (9.7)
(9.7)
Для многослойной цилиндрической стенки величина кl имеет вид:
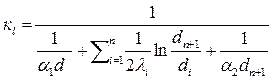 . (9.8)
. (9.8)
Дата добавления: 2015-02-16; просмотров: 2846;
