Теоретические сведения. Зачастую для решения одной и той же задачи можно использовать разные средства языка.

Зачастую для решения одной и той же задачи можно использовать разные средства языка.

В качестве примеров рассмотрим классические задачи вычисления корней линейного и квадратного уравнений.

Пример 1. Составьте программу для решения уравнения вида 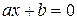на множестве действительных чисел. Исходные данные – значения коэффициентов а, b вводятся пользователем с клавиатуры.

Известно, что при разных значениях коэффициентов a и b задача вычисления корней должна решаться по разным правилам. Перечислим возможные варианты:

а!=0 – уравнение имеет единственный корень, который вычисляется по формуле x=a/b;

а==0, b!=0 – уравнение примет вид 0 = b, которое при ненулевом значении b корней не имеет;

а==0, b==0 – уравнение примет вид 0 = 0, решением которого является множество действительных чисел.

Блок-схема данной программы будет выглядеть следующим образом:

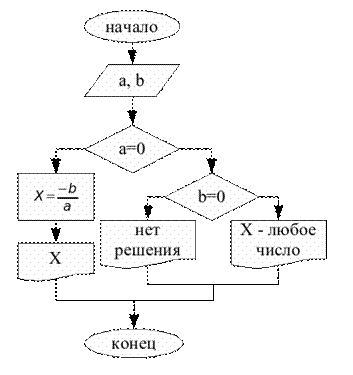
// Программа для решения линейного уравнения

#include <stdio.h>

#include <math.h>

void main () {

float a,b,x;

printf ("Введите коэффициенты линейного уравнения: ");

printf ("\n a = "); scanf ("%f",&a);

printf (" b = "); scanf ("%f",&b);

printf ("\nРешение линейного уравнения: ");

if (a==0)

if (b==0) printf ("Х - любое число");

else printf ("нет решения");

else {

x=-b/a;

printf ("\n X = %f",x);

}

}

Пример 2. Составьте программу для решения квадратного уравнения 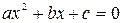на множестве комплексных чисел. Исходные данные – действительные значения коэффициентов а, b, с вводятся пользователем с клавиатуры.

Известно, что при разных значениях коэффициентов a, b, с задача вычисления корней должна решаться по разным правилам. Перечислим возможные варианты:

а==0 – линейное уравнение;

а!=0, b*b-4*a*c>0 – два различных действительных корня;

а!=0, b*b-4*a*c=0 – два совпадающих действительных корня;

а!=0, b*b-4*a*c<0 – два комплексных корня.

В случаях, когда a! =0 справедлива формула: .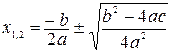

С ее помощью при положительном дискриминанте 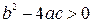вычисляются два действительных корня. При отрицательном дискриминанте, т.е. когда 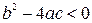, комплексные корни можно определить так: 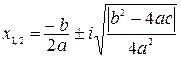, где i – мнимая единица.

Отметим, что в языке Си комплексную величину можно представить двумя переменными, соответствующими ее действительной и мнимой частям.

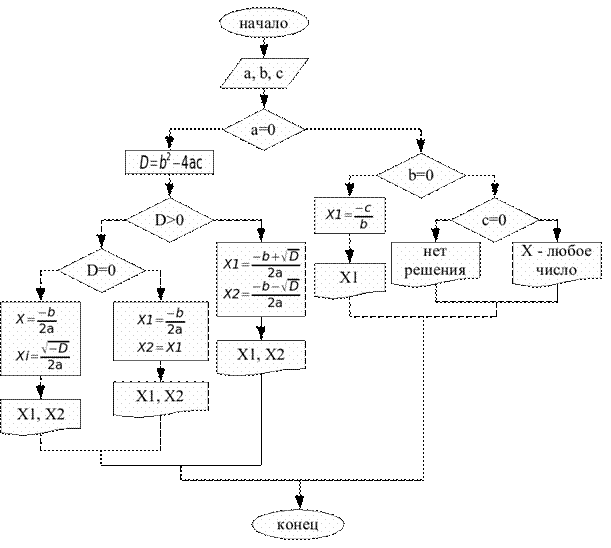
Блок-схема данной программы будет выглядеть следующим образом:

// Программа для решения квадратного уравнения

#include <stdio.h>

#include <math.h>

void main () {

float a,b,c,x1,x2,x,xi,d;

printf ("Введите коэффициенты квадратного уравнения: ");

printf ("\n a = "); scanf ("%f",&a);

printf (" b = "); scanf ("%f",&b);

printf (" c = "); scanf ("%f",&c);

printf ("\nРешение квадратного уравнения: ");

if (a==0)

if (b==0)

if (c==0) printf ("Х - любое число");

else printf ("нет решения");

else {

x1=-c/b;

printf ("\n X = %f",x1);

}

else {

d=b*b-4*a*c;

if (d>0) {

x1=(-b-sqrt(d))/(2*a);

x2=(-b+sqrt(d))/(2*a);

printf ("\n X1 = %f \n X2 = %f ",x1,x2);

}

else

if (d==0) {

x1=-b/(2*a);

printf ("\n X1 = X2 = %f",x1);

}

else{

x=-b/(2*a);

xi=sqrt(-d)/2/a;

printf ("\n X1 = %f + %f i \n X2 = %f - %f i ",

x,xi,x,xi);

}

}

}

Задания

1.Составьте программу для решения задачи. Даны три действительных числа a, b, c. Определите, существует ли треугольник с такими сторонами, а, если существует, то укажите его вид (прямоугольный, остроугольный, тупоугольный).

2.Составьте программу для решения задачи. В магазине действует система скидок: при покупке товара на сумму свыше 200 рублей – скидка 2%, свыше 500 рублей – 3%, свыше 1000 рублей – 10%. Определите, какую сумму должен оплатить покупатель, если им куплен товар на сумму N рублей.

Домашние задания

1.Наберите код программ из Примеров 1 и 2. Сохраните коды программ. Выполните компиляцию и запуск программ. Введите свои данные в качестве входных.

2.Составьте программу для решения биквадратного уравнения вида 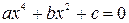для действительных x. Исходные данные – значения коэффициентов а, b, с вводятся пользователем с клавиатуры.

3. Индивидуальное задание №1. Номер варианта определяется по журналу. Разработайте программу для вычисления у с учетом области определения функции. Числа a, b, c вводятся с клавиатуры.

4. Индивидуальное задание №2. Номер варианта определяется по журналу. Составьте программу для решения задачи.

Варианты индивидуального задания №1

№	Задание
1.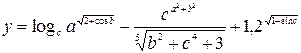
2.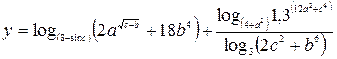
3.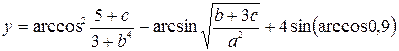
4.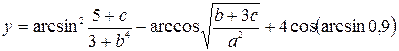
5.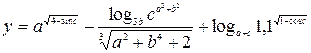
6.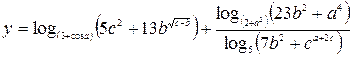
7.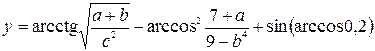
8.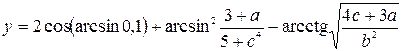
9.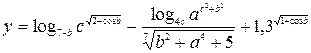
10.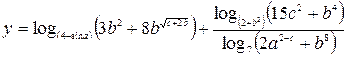
11.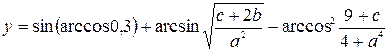
12.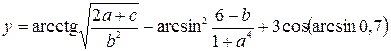
13.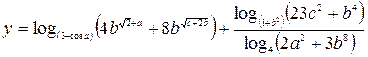
14.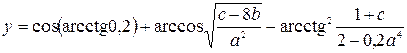
15.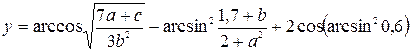
16.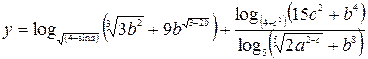
17.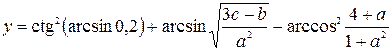
18.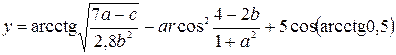
19.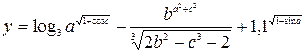
20.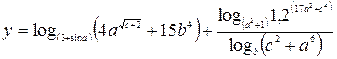
21.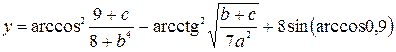
22.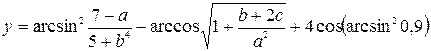
23.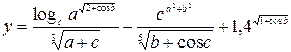
24.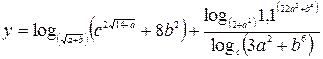
25.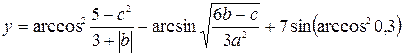
26.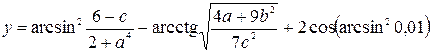
27.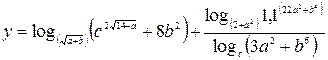
28.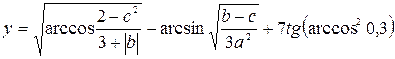

Варианты индивидуального задания №2

№	Задание
1.	Составить программу, которая вычисляет оптимальный вес пользователя, сравнивает его с реальным весом (его вводит пользователь) и выдает рекомендацию о необходимости поправиться или похудеть на некоторое количество килограммов или сообщает о том, что пользователь в идеальной форме. Оптимальный вес вычисляется по формуле: рост (в см) – 100.
2.	Билеты нумеруются шестизначными целыми числами. Билет считается «счастливым», если сумма трех первых цифр его номера рана сумме трех последних цифр. Определите, является ли «счастливым» билет с номером n.
3.	Дано трехзначное число, у которого число единиц не превосходит числа сотен. Проверить, является ли оно палиндромом, т.е. число, которое одинаково читается слева направо и справа налево. Если не является, то вывести ближайшее следующее число-палиндром.
4.	Скорость передачи данных по сети v Кбит/с, за подключение к сети за сеанс связи взимается плата а копеек. Требуется получить k Мбайт информации, оплачено на данный момент n минут работы в сети. Будет ли получена требуемая информация, если сеть работает стабильно?
5.	Решите уравнение вида arcsin x = a относительно х. Входным данным является значение а.
6.	С клавиатуры вводится целое число х их промежутка [100, 9999]. Если число четырехзначное, то найти сумму его цифр, а если трехзначное, то произведение цифр числа.
7.	Удвоить трехзначное число, введенное с клавиатуры, если оно содержит в своей записи хотя бы одну 1, и возвести в квадрат в противном случае.
8.	Дано 5-значное число. Определить, упорядочены ли по возрастанию цифры в записи этого числа. Например, в числе 13789 цифры упорядочены по возрастанию, а в числе 34609 – нет.
9.	Даны три числа. Определить вид треугольника, если он существует (равносторонний, равнобедренный, разносторонний), длины сторон которого равны введенным числам.
10.	Даны три целых числа. Найти среднее из них. Средним назовем число, которое больше наименьшего из данных чисел, но меньше наибольшего.
11.	Составьте программу для определения вида параллелограмма по прилежащим сторонам a, b и углу между ними х (в градусах). Определить один из видов: ромб, прямоугольник, квадрат, параллелограмм общего вида.
12.	Составьте программу для определения вида четырехугольника, у которого две стороны параллельны. Определить по двум прилежащим к одной из параллельных сторон углам х и y, к какому из четырех видов относится четырехугольник: обыкновенная трапеция, прямоугольная трапеция, равнобедренная трапеция, прямоугольник, параллелограмм.
13.	Составить программу определения стоимости разговора по телефону с учетом скидки 20%, предоставляемой по субботам и воскресеньям. Минута разговора стоит 2,3 руб. Входными данными являются n – номер дня недели (1 – понедельник и т.д.) и k – количество минут разговора.
14.	Посчитать сумму только положительных из трех данных чисел.
15.	С клавиатуры вводиться два трехзначных числа. Возвести первое число в квадрат, а из второго извлечь квадратный корень, если хотя бы у одного из чисел средняя цифра четная. В противном случае из первого числа извлечь квадратный корень, а второе возвести в квадрат. Вывести измененные числа на экран.
16.	Дано двузначное число. Составить программу определения, является ли сумма его цифр двузначным числом. Если нет, то через сколько чисел встретится первое двузначное число, удовлетворяющее этому условию.
17.	Даны три переменные: X, Y, Z. Если их значения упорядочены по убыванию, то удвоить их; в противном случае заменить значение каждой переменной на противоположное.
18.	Даны три переменные: X, Y, Z. Если их значения упорядочены по возрастанию или убыванию, то удвоить их; в противном случае заменить значение каждой переменной на противоположное.
19.	Даны целочисленные координаты точки на плоскости. Если точка не лежит на координатных осях, то вывести 0. Если точка совпадает с началом координат, то вывести 1. Если точка не совпадает с началом координат, но лежит на оси 0X или 0Y, то вывести соответственно 2 или 3.
20.	Дан номер некоторого года (положительное целое число). Вывести соответствующий ему номер столетия, учитывая, что, к примеру, началом 20 столетия был 1901 год.
21.	Дан номер некоторого года (положительное целое число). Вывести число дней в этом году, учитывая, что обычный год насчитывает 365 дней, а високосный – 366 дней. Високосным считается год, делящийся на 4, за исключением тех годов, которые делятся на 100 и не делятся на 400 (например, годы 300, 1300 и 1900 не являются високосными, а 1200 и 2000 – являются).
22.	Дано целое число, лежащее в диапазоне от –999 до 999. Вывести строку – словесное описание данного числа вида «отрицательное двузначное число», «нулевое число», «положительное однозначное число» и т.д.
23.	Дано целое число, лежащее в диапазоне от 1 до 9999. Вывести строку – словесное описание данного числа вида «четное двузначное число», «нечетное четырехзначное число» и т.д.
24.	Телефонная компания взимает плату за пользование телефонной линией по следующему тарифу: до 120 минут разговоров включительно входит в абонентскую плату 100 рублей, за каждую минуту свыше 120 до 300 минут включительно – по 1 рублю, свыше 300 минут – по 1,5 рубля за минуту. Определите размер телефонной платы за n минут разговора.
25.	Определите оценку (5, 4, 3, 2) за экзамен по математике по следующей шкале: 80 – 100 баллов – «5», 55 – 79 баллов – «4», 30 – 54 баллов – «3», остальное соответствует «2». Входными данными является количество набранных баллов b.
26.	Решите уравнение вида cos x =a относительно х. Входным данным является значение а.
27.	Найдите число решений системы в зависимости от параметров a и b:
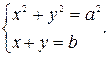
28.	Решите уравнение вида 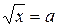относительно х. Входным данным является значение а.