Задание 3
Обработать методом дисперсионного анализа содержание сырой клейковины в зерне яровой пшеницы (Саратовская 29) однофакторного полевого опыта, заложенного методом рендомизированных повторений. Установите существенность различий между вариантами опыта.
Решение. Шаг 1. Составляем исходную таблицу (содержания сырой клейковины в зерне яровой пшеницы по вариантам) и вычисляем соответствующие показатели (табл. 1).
Таблица 1. Исходная таблица.
| Вариант опыта | Содержание сырой клейковины (%) по повторностям | 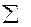 V V
| 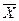
| |||
| 14(St) | 30,8 | 31,5 | 28,2 | 29,0 | 119,5 | 29,9 |
| 28,6 | 25,3 | 23,4 | 32,5 | 109,8 | 27,4 | |
| 31,8 | 29,3 | 31,5 | 28,8 | 121,4 | 30,3 | |
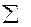 P P
| 91,2 | 86,1 | 83,1 | 90,3 | ( 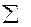 Х) = =350,7 Х) = =350,7
| 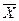 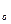 = 29,2 = 29,2
|
Суммы квадратов отклонений с l-вариантами и n-повторениями - находят обычно в такой последовательности.
Сумму по вариантам находим сложением данных содержания
сырой клейковины всех четырех повторений каждого варианта (каждую строку): 30,8 + 31,5 + 28,2 + 29,0 = 119,5
28,6 + 25,3 + 23,4 + 32,5 = 109,8
31,8 + 29,3 + 31,5 + 28,8 = 121,4
Сумму по повторениям находим сложением данных содержания сырой клейковины каждого столбца по всем вариантам:
30,8 + 28,6 + 31,8 = 91,2
31,5 + 25,3 + 29,3 = 86,1
28,2 + 23,4 + 31,5 = 83,1
29,0 + 32,5 + 28,8 = 90,3
Сумма по вариантам ( 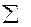 Р) равна сумме по повторениям (
Р) равна сумме по повторениям ( 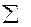 V) и сумме всего содержания сырой клейковины (
V) и сумме всего содержания сырой клейковины ( 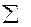 Х) = 350,7
Х) = 350,7
Средние арифметические находим по каждому варианту делением сумм по вариантам на число повторений: 119,5 : 4 = 29,9
109,8 : 4 = 27,4
121,4 : 4 = 30,3
Для нахождения среднего содержания сырой клейковины в зерне по всему полевому опыту 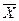
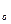 делят сумму всего содержания сырой клейковины
делят сумму всего содержания сырой клейковины 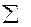 Х на общее число делянок в опыте
Х на общее число делянок в опыте
N= l x n = 3 x 4 =12
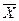
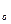 = 350,7 : 12 = 29,2 %
= 350,7 : 12 = 29,2 %
Шаг 2. Для нахождения квадратов чисел составим табл. 2.
Таблица 2. Квадраты чисел (содержание сырой клейковины)
| Вариант | Повторения | |||
| 14(St) | 948,64 | 992,25 | 795,24 | 841,00 |
| 817,96 | 640,09 | 547,56 | 1056,25 | |
| 1011,24 | 858,49 | 992,25 | 829,44 |
Шаг 3. Вычисляем суммы квадратов чисел.
Находим сумму квадратов всех чисел:
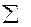 Х
Х  = 30,8
= 30,8 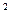 + 31,5
+ 31,5 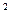 + 28,2
+ 28,2 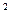 + 29,0
+ 29,0 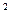 + 28,6
+ 28,6 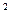 + 25,3
+ 25,3 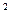 + 23,4
+ 23,4 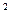 + 32,5
+ 32,5 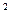 + 31,8
+ 31,8 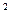 + 29,3
+ 29,3 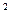 + 31,5
+ 31,5  + 28,8
+ 28,8 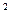 = 10330,41
= 10330,41
Находим сумму квадратов по вариантам:
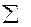 V
V  = 119,5
= 119,5  + 109,8
+ 109,8  + 121,4
+ 121,4  = 14280,25 + 12056,04 + 14737,96 = =41074,25
= 14280,25 + 12056,04 + 14737,96 = =41074,25
Находим сумму квадратов по повторениям:
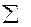 P
P  = 91,2
= 91,2  + 86,1
+ 86,1  + 83,1
+ 83,1  + 90,3
+ 90,3  = 8317,44 + 7413,21 + 6905,61 + 8154,09 = 30790,35
= 8317,44 + 7413,21 + 6905,61 + 8154,09 = 30790,35
Шаг 4. Общее число наблюдений определяем умножением числа вариантов l на число повторений n
N= l x n = 3 x 4 =12
Шаг 5. Имея квадраты чисел, рассчитываем следующие показатели:
1) С - корректирующий фактор (поправка).
Для нашего примера:
С = ( 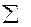 Х) 2 : N = 350,72 : 12 = 10249,2
Х) 2 : N = 350,72 : 12 = 10249,2
2) С 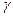 - общее число наблюдений находим по формуле:
- общее число наблюдений находим по формуле:
С 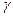 =
= 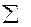 Х
Х  - С = 10330,41 - 10249,2 = 81,21
- С = 10330,41 - 10249,2 = 81,21
3) Ср – варьирование вариантов определяем по формуле:
Ср = 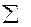 P
P  : l – С = 30790,35 : 3 - 10249,2 = 14,25
: l – С = 30790,35 : 3 - 10249,2 = 14,25
4) Сv - варьирование вариантов определяем по формуле:
Сv = 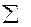 V
V  : n - С = 41074,25 : 4 - 10249,2 = 19,36
: n - С = 41074,25 : 4 - 10249,2 = 19,36
5) Cz - варьирование остаточное находим по формуле:
Cz = С 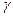 - Сv - Ср = 81,21 - 19,36 - 14,25 = 47,6
- Сv - Ср = 81,21 - 19,36 - 14,25 = 47,6
Шаг 6. Для выяснения существенности различий между вариантами опыта данные сведем в таблицу 3.
Таблица 3. Результаты дисперсионного анализа
| Вид варьирования | Сумма квадратов отклонений | Число степеней свободы | Средний квадрат (дисперсия) S 
| F | |
| Факт. | |||||
Общее (С 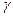 ) )
| 81,21 | N - 1= 11 | -- | -- | -- |
| Повторений (Ср) | 14,25 | n – 1= 3 | -- | -- | -- |
| Вариантов (Сv) | 19,36 | l – 1 = 2 | (S  v) = 9,68 v) = 9,68
| 1,22 | 5,14 |
| Остаточное (ошибки) (Cz) | 47,6 | (n – 1) x (l – 1) = 6 | (S  z) = 7,9 z) = 7,9
| -- | -- |
Число степеней свободы для общего варьирования определяют общим числом наблюдений в опыте без единицы: N - 1 = 12 – 1 = 11
Также определяют степени свободы для повторений и вариантов. Число степеней свободы для остаточного варьирования определяют умножением чисел степеней свободы вариантов и повторений: 3х2=6.
Дисперсию для различных видов варьирования находят делением сумм квадратов на число степеней свободы:
S  v = Сv/ l – 1= 19,36 : 2 =9,68
v = Сv/ l – 1= 19,36 : 2 =9,68
S  z = Cz / (n – 1) x (l – 1) = 47,6 : 6 = 7,9
z = Cz / (n – 1) x (l – 1) = 47,6 : 6 = 7,9
Критерий Фишера (F 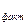 ) определяем делением дисперсии вариантов на дисперсию ошибок: F
) определяем делением дисперсии вариантов на дисперсию ошибок: F 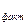 = S
= S  v / S
v / S  z = 9,68 : 7,9 = 1,22
z = 9,68 : 7,9 = 1,22
Шаг 7. Вывод: Если F 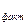 меньше F05 (1,22< 5,14), то между вариантами опыта нет различий, и нулевая гипотеза подтверждается.
меньше F05 (1,22< 5,14), то между вариантами опыта нет различий, и нулевая гипотеза подтверждается.
Дата добавления: 2015-02-16; просмотров: 1521;
