Круговое вращающееся магнитное поле двух- и трехфазной обмоток
Круговым вращающимся магнитным полем называется поле, вектор магнитной индукции которого, не изменяясь по модулю, вращается в пространстве с постоянной угловой частотой.
Для создания кругового вращающегося поля необходимо выполнение двух условий:
1. Оси катушек должны быть сдвинуты в пространстве друг относительно друга на определенный угол (для двухфазной системы – на 900, для трехфазной – на 1200).
2. Токи, питающие катушки, должны быть сдвинуты по фазе соответственно пространственному смещению катушек.
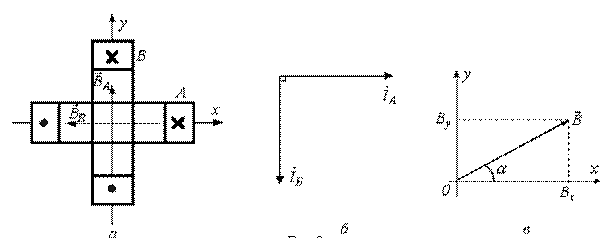
Рассмотрим получение кругового вращающегося магнитного поля в случае двухфазной системы Тесла (рис. 7.10,а).
При пропускании через катушки гармонических токов каждая из них в соответствии с вышесказанным будет создавать пульсирующее магнитное поле. Векторы 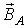 и
и 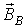 , характеризующие эти поля, направлены вдоль осей соответствующих катушек, а их амплитуды изменяются также по гармоническому закону. Если ток в катушке В отстает от тока в катушке А на 900 (см. рис. 7.10,б), то
, характеризующие эти поля, направлены вдоль осей соответствующих катушек, а их амплитуды изменяются также по гармоническому закону. Если ток в катушке В отстает от тока в катушке А на 900 (см. рис. 7.10,б), то 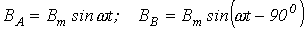 .
.
Найдем проекции результирующего вектора магнитной индукции 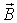 на оси x и y декартовой системы координат, связанной с осями катушек:
на оси x и y декартовой системы координат, связанной с осями катушек:
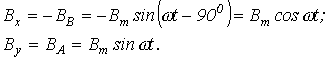
Модуль результирующего вектора магнитной индукции в соответствии с рис. 7.10,в равен
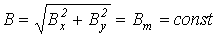
при этом для тангенса угла a , образованного этим вектором с осью абсцисс, можно записать
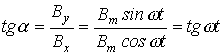 ,
,
Откуда
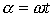 . .
| (2) |
Полученные соотношения (1) и (2) показывают, что вектор результирующего магнитного поля неизменен по модулю и вращается в пространстве с постоянной угловой частотой 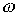 , описывая окружность, что соответствует круговому вращающемуся полю.
, описывая окружность, что соответствует круговому вращающемуся полю.
Покажем, что симметричная трехфазная система катушек (см. рис. 3,а) также позволяет получить круговое вращающееся магнитное поле.
Каждая из катушек А, В и С при пропускании по ним гармонических токов создает пульсирующее магнитное поле. Векторная диаграмма в пространстве для этих полей представлена на рис. 3,б. Для проекций результирующего вектора магнитной индукции на
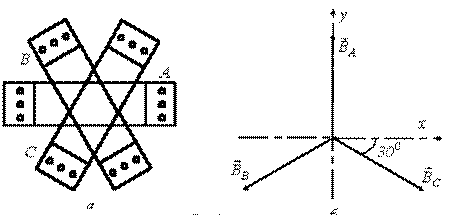
Рис. 7.10
оси декартовой системы координат, ось y у которой совмещена с магнитной осью фазы А, можно записать
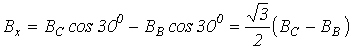 ; ;
| (3) |
 . .
| (4) |
Приведенные соотношения учитывают пространственное расположение катушек, но они также питаются трехфазной системой токов с временным сдвигом по фазе на 1200. Поэтому для мгновенных значений индукций катушек имеют место соотношения
 ;
; 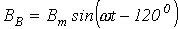 ;
; 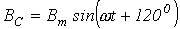 .
.
Подставив эти выражения в (3) и (4), получим:
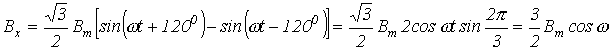 ; ;
| (5) |

| (6) |
В соответствии с (5) и (6) и рис. 2,в для модуля вектора магнитной индукции результирующего поля трех катушек с током можно записать:
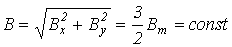 ,
,
а сам вектор 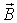 составляет с осью х угол a, для которого
составляет с осью х угол a, для которого
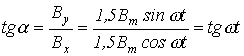 ,
,
откуда
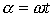 .
.
Таким образом, и в данном случае имеет место неизменный по модулю вектор магнитной индукции, вращающийся в пространстве с постоянной угловой частотой 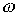 , что соответствует круговому полю.
, что соответствует круговому полю.
Вопросы к теме
1. Что такое магнитное поле и магнитная цепь?
2. Каковы основные характеристики и законы магнитного поля?
3. Каковы свойства ферромагнитных материалов в постоянном и переменном магнитном поле?
4. В чем состоят и как реализуются прямая и обратная задачи расчета магнитной цепи при постоянном воздействии?
5. Знать какие процессы происходят в катушке с ферромагнитным сердечником при гармоническом воздействии. Как они отражаются в эквивалентной схеме?
6. Как возникает пульсирующее магнитное поле. Как его можно описать с помощью двух вращающихся?
7. Как возникает вращающееся круговое поле в системе двух катушек?
8. Как возникает вращающееся круговое поле в системе трех катушек? Каковы условия возникновения кругового вращающегося магнитного поля?
Дата добавления: 2015-02-16; просмотров: 1138;
