Теплопередача через наружные ограждения.

В простейшем виде расчетная модель ограждающей конструкции здания представляет собой бесконечно протяженную плоскую стенку, ограниченную параллельными поверхностями и разделяющую воздушные среды с разными температурами.

В этом и последующих параграфах будет рассматриваться холодный период, когда температура наружного воздуха намного ниже температуры внутреннего. Считаем, что эти температуры заданы и не меняются с течением времени. То есть процесс теплопроводности через стенку является стационарным.

Ограждающая конструкция может быть однородной, если она выполнена из одного материала, и многослойной.

Рассмотрим однородную стенку толщиной δ, коэффициент теплопроводности которой равен λ. На внутренней и наружной поверхностях поддерживаются постоянные температуры t_si и t_se. Очевидно, что при таких условиях температура внутри стенки будет изменяться только в направлении, перпендикулярном поверхности стенки, то есть по оси X. Температурное поле одномерно и стационарно, а изотермы перпендикулярны оси X (рис.2.2).

Выделим внутри стенки слой толщиной dx, ограниченный двумя изотермами. В пределах этого слоя

температура изменяется на dt. На основании закона Фурье уравнение (2.4) для этого случая можно записать как

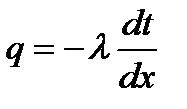, откуда

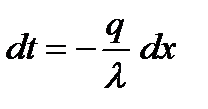(2.5)

Величина плотности теплового потока q при стационарных условиях постоянна в каждом сечении. Поэтому, интегрируя получим:

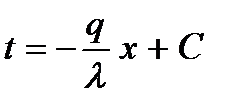. (2.6)

Постоянная С определяется из граничных условий, а именно: при x = 0 t = t_si= C, при x = δ t = t_se.

Подставим эти значения в (2.6) и получим выражение для плотности теплового потока:

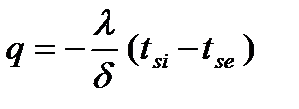. (2.7)

Можно сделать вывод: количество теплоты, проходящее через единицу поверхности стенки в единицу времени, прямо пропорционально коэффициенту теплопроводности λ, разности температур на поверхностях стенки (t_si - t_se) и обратно пропорционально толщине стенки δ.

Формулу (2.7) можно записать как

.

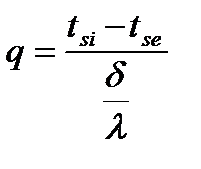Отношение δ/λ называется термическим сопротивлением однородного ограждения или отдельного слоя в многослойном ограждении

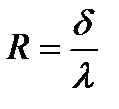. (2.8)

Тогда (2.7) можно записать как

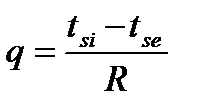, (2.9)

откуда

.

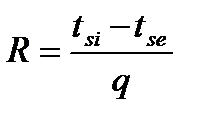Термическое сопротивление численно равно разности температур, при которой через стенку проходит тепловой поток плотностью 1 Вт/м², и измеряется в м²·ºС/Вт.

Для многослойной конструкции, состоящей из n слоев, термическое сопротивление равно сумме сопротивлений отдельных слоев

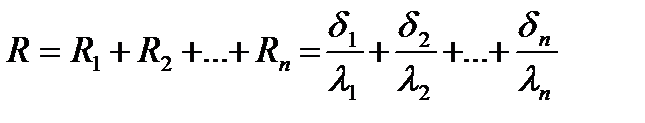, (2.10)

где δ_i – толщины отдельных слоев, м; λ_i – коэффициенты теплопроводности материалов этих слоев, Вт/(м · ˚C); i = 1, 2,…, n.