Деструкция полимеров.

.

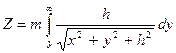Очевидно,

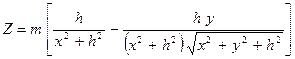. (10.24)

В точке начала координат ( х=0 ) при h=-1 получим для поправок при у=2 значение 11%, при у=3 – 5% и при у=5 – 2%. Если учесть необходимость трансформации и по другую сторону поля, то величину поправок следует удвоить.

Итак, для трансформации поля необходимо по формуле (10.24) вычислить поправки для различных значений х. В итоге получим график с несколько уменьшенной локализацией.

10.9. Применение математического моделирования

Решение любой геологической задачи магниторазведкой начинается с имитации поисковых и разведочных объектов, с представления их физико-геологическими моделями и соответствующими им математическими моделями. На начальном этапе необходимо сформулировать постановку задачи, т.е. дать содержательное описание. Физико-геологическая модель должна отражать взаимосвязь представленных магнитных свойств и параметров объекта с ожидаемыми магнитными полями. Магнитные параметры выбираются в соответствии с условиями образования магнетизма горных пород и с учетом геометрической формы изучаемого объекта. Модель в магниторазведке можно представить как геолого-магнитную модель.

При задании математической модели словесное описание задачи должно быть переведено на математический язык. Математическая модель описывает с некоторой степенью приближения реальную систему в виде формул, уравнений и неравенств. Дальнейшая работа сводится к изучению модели, к исследованиям, под которыми следует понимать процесс перебора свойств изучаемой системы путем проведения экспериментов над моделью.

Для решения прогнозных геологических задач с использованием принципа аналогий привлекаются «натурные» площади, соответствующие хорошо изученным природным объектам, которые можно принять за эталонные. Для них разрабатываются специальные эталонные физико-геологические модели (ФГМ) объектов, для которых на ЭВМ рассматриваются различные ситуации при разных параметрах модели, обеспечивающие вариации этих значений и позволяющие выполнить расчет любого числа реализаций. Моделирование основано на решении прямых задач применительно к построенной физико-геологической модели, наделенной магнитными свойствами возмущающих объектов, с целью изучения варьируемости аномальных эффектов и сравнения рассчитанного и наблюденного полей.

Принцип модельности, основанный на совокупности любых формализованных допущениях, широко применяется в интерпретационном процессе магнитных аномалий. Однако заданный флуктуирующий разброс параметров объекта впоследствии дает множество эквивалентных распределений источников, что затрудняет выборку того или иного признака. Необходимо учитывать требования, предъявляемые к интерпретационным моделям, которые зависят от поставленных геологических задач. Они должны удовлетворять условиям решения обратной задачи: единственности, устойчивости и корректности, а также соответствовать имеющимся представлениям о геологической структуре и физических свойствах магнитных источников. Выполнить все эти условия очень трудно.

Полное соблюдение этих требований для магниторазведки почти невозможно. Необходимо вводить набор ограничений на параметры источников. Иногда предлагают для аппроксимации поля использовать сеточные модели геологической среды, когда моделирование поля осуществляется большим количеством источников с фиксированными геометрическими параметрами. В качестве элементарных источников целесообразно использовать тела простой формы (шар, шток), аномальные эффекты от которых вычисляются путем небольшого числа арифметических операций.

В настоящее время при интерпретации магнитных аномалий внедряется истокообразная аппроксимация магнитного поля, которая разработана с использованием эквивалентных моделей геологической среды, а также адекватных и смешанных моделей.

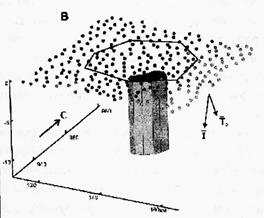
Рис. 10.20. Подбор модели по магнитному полю

(по П.С.Бабаянцу):

а – карта магнитных аномалий DТ;, в – трехмерная модель блока

Адекватной является модель, в которой обеспечивается аппроксимация намагниченности геологического объекта с высокой точностью. Эквивалентная модель не всегда обеспечивает аппроксимацию намагниченности магнитного тела, но обеспечивает требуемую степень близости полей. Смешанная модель обеспечивает требуемую степень близости полей и аппроксимацию природной намагниченности внутри геологической среды.

На рис. 10.20 представлен пример интерпретации магнитной аномалии над одним из блоков в кристаллическом фундаменте Московской синеклизы. Подобранная глубина залегания верхней кромки трехмерной модели блока соответствует уровню – 1200 м, что точно согласуется с реальной глубиной кровли кристаллического фундамента.

В последнее время для выбора эталонной модели (ФГМ) объекта рекомендуется превращать ее в стохастическую модель, которая обеспечивает многочисленные вариации значений входных параметров и ведет расчет любого числа реализаций /16/. Для перехода к стохастическим ФГМ объектов используется программный комплекс INTERACT /19/. В программе предусмотрено аналитическое вычисление реализаций магнитных Z и DТ полей от двухмерных объектов сложной формы с флуктуирующим вектором параметров. Поля Z и DТ считаются намагниченными современным полем Земли. Учитывается также остаточная намагниченность. Кроме наблюденных полей вычисляются их первые производные, а также дополнительные трансформанты полей.

Математическое моделирование является универсальным способом для трансформирования магнитных полей. Идея способа довольно проста. Отвлекаясь от геолого-геофизической природы аномального поля, при помощи набора элементарных моделей можно рассчитать эффект, аппроксимирующий значения наблюденных аномалий, а затем, используя этот набор, в порядке решения прямых задач вычислить другие, интересующие нас элементы поля. Точность решения зависит от точности аппроксимации.

Очень эффективно операция аппроксимации реализуется на ПК. Прежде всего, до применения ПК необходимо определить для данного поля область существования выпуклого тела. Разбивая эту область на квадратные клетки, затем заменяя клетки с такой же площадью элементарными моделями, программируем вычисление и далее в автоматизированном режиме ведем расчеты. В итоге получаем распределение намагниченных масс, которое своим действием аппроксимирует наблюденное поле. Трансформируемые поля получаем решением прямых задач.

Способы трансформации магнитного поля обладают широкими возможностями. Рассмотренные в этой главе задачи (исключая задачи сглаживания и приведения трехмерного поля к двухмерному) успешно могут быть решены с помощью моделирования. В частности, вычисление высших производных при помощи численного дифференцирования может быть выполнено с большой достоверностью путем математического моделирования с использованием формулы

.

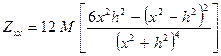Следует отметить, что точность результатов, полученных таким образом, будет значительно выше.

Представляют определенный интерес для интерпретации и градиенты первого порядка

,

.

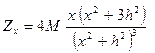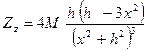При геологической интерпретации часто возникает необходимость в использовании величин, которые не измеряются, а вычисляются различными численными методами. Заслуживает внимания магнитный потенциал

,

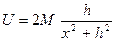где h – глубина оси центра. Потенциал может быть использован для прямого определения поперечного сечения аномального тела.

Математическое моделирование, будучи операцией сугубо формальной, не решает задач геологической интерпретации. Искомое распределение намагниченных масс может быть найдено при решении иного класса обратных задач с использованием априорной информации.

Роль модельныхпредставлений в процессе интерпретации исключительно велика, они фактически определяют выбор комплекса методов решения обратной задачи. В процессе интерпретации переходим от более низкого уровня модельных представлений к более высокому. Извлечь из наблюденных значений поля какую-либо информацию без использования модельных представлений нельзя.

В.Н. Страхов /33/ пишет, что геофизика – наука опытная, процесс интерпретации есть процесс познания. К чему бы мы ни стремились, неформализованное мышление, опыт и интуиция имели и всегда будут иметь определяющее значение при решении конкретных геологических задач, особенно на этапах принятия решения.

Четкого и исчерпывающего определения модели сейчас нет. Ясны лишь следующие моменты: модель среды и модель поля – разные понятия, хотя они существуют и связаны между собой. Модельные представления могут существовать в различной форме и на различных уровнях – от неопределенно-интуитивных до формализовано-аналитических.

Информация об исследуемых полях, которую называют дополнительной, всегда неточная, она является продуктом переработки конкретных фактов на основе неформализованного мышления, опыта и интуиции. Ее использование предопределяет результат интерпретации и может вести к неверному итогу. Делая меньше допущений, получаем менее полный, но более объективный результат.

По разработанным постоянно действующим моделям типовых месторождений полезных ископаемых создаются программные обрабатывающие и интерпретирующие комплексы. Среди ведущих российских компаний известно акционерное общество «Пангея», использующее системы технологии Многомерной интерпретации. Они успешно демонстрирует возможности применения компьютерных интерпретирующих систем для прогноза залежей углеводородного сырья, а с 1998 г. эффективно ведут интерпретацию материалов магниторазведки при поисках, разведке и анализе геологического строения месторождений твердых полезных ископаемых.

В основу обрабатывающего пакета положены оригинальные алгоритмы, с помощью которых можно определять распределение намагниченности в слое между двумя заданными контактными поверхностями, оценивать рельеф горизонтальных границ раздела, выявлять кристаллический фундамент и структурные поверхности в составе осадочного чехла, вычислять трансформанты потенциальных полей.

Указанные алгоритмы базируются на преобразованиях спектров аномального поля. Программы позволяют выполнять аналитическое продолжение поля в верхнее и нижнее полупространства, вычислять высшие производные любого порядка и осуществлять различную фильтрацию магнитных наблюдений.

Из зарубежных компьютерных программных технологий по обработке и интерпретации геолого-геофизической информации широко известны разработки Канадских фирмы «Geosoft».

Деструкция полимеров.