Примеры решения задач
Задача 1. Конденсатор ёмкости С1, заряженный до разности потенциалов U, подключили параллельно к концам системы из двух последовательно соединённых незаряженных конденсаторов, ёмкости которых С2 и С3. Какой заряд протечёт при этом по соединительным проводам?
Решение. Вначале заряд первого конденсатора был равен q = C1U. После подключения этот заряд перераспределился между конденсаторами таким образом, чтобы напряжения на первом конденсаторе и подключённой батарее были бы одинаковыми. Имеем:
q1 + q2 = q, 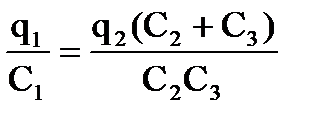 ,
,
где q1 − заряд на первом конденсаторе после подключения, а q2 − заряд на подключённой батарее. Решая эти два уравнения, найдём q1и протёкший зарядΔq = q – q1= 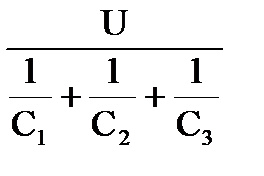
Задача 2. К источнику с э.д.с. U подключили последовательно два воздушных конденсатора, каждый ёмкостью С. Затем один из конденсаторов заполнили однородным диэлектриком с проницаемостью ε. Во сколько раз уменьшилась напряжённость электрического поля в этом конденсаторе? Какой заряд пройдёт через источник?
Решение. Найдём сначала протёкший заряд. Заряд конденсатора до заполнения диэлектриком равен 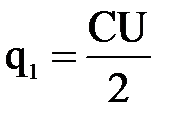 , а заряд после заполнения
, а заряд после заполнения
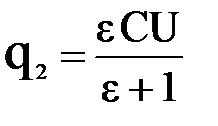 .
.
Отсюда протёкший заряд равен Δq = q2 – q1.
Напряжённость поля сначала равна 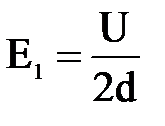 , где d − расстояние между пластинами. После введения диэлектрика она становится равной
, где d − расстояние между пластинами. После введения диэлектрика она становится равной
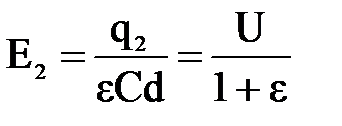 . Отсюда
. Отсюда 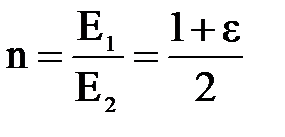 .
.
Ответ: 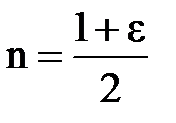 ,
, 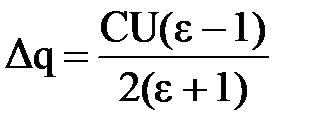 .
.
Задача 3.Диэлектрик с диэлектрической проницаемостью ε заполняет пространство между обкладками плоского конденсатора. Емкость конденсатора равна С. Конденсатор заряжен до разности потенциалов U и отключен от источника напряжения. Затем диэлектрик медленно удаляют из конденсатора. Какую работу надо при этом совершить ?
Решение: Так как конденсатор отключается от источника напряжения, заряд на его обкладках не меняется. Энергия, запасенная конденсатором, равна
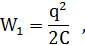
где С — емкость конденсатора с диэлектриком. После того как диэлектрик удален, емкость конденсатора уменьшается в ε раз. Следовательно,
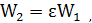
т. е. запасенная конденсатором энергия увеличится в ε раз. Для увеличения энергии необходимо совершить работу по удалению диэлектрика, величина которой равна:
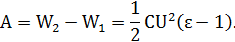
То, что для удаления диэлектрика нужно совершить работу, ясно из общих соображений: между индуцированным на диэлектрике зарядом и зарядом пластин действует притяжение, против сил которого и совершается внешняя работа при удалении диэлектрика из конденсатора.
Задача 4. Пространство между обкладками плоского конденсатора заполнено последовательно двумя диэлектрическими слоями 1 и 2 с толщинами d1 и d2 и с проницаемостями ε1иε2.Площадь каждой обкладки равна S. Найти:а) ёмкость конденсатора;б) плотность σ / связанных зарядов на границе раздела диэлектрических слоёв, если напряжение на конденсаторе равно U и электрическое поле направлено от слоя 1 к слою 2.
Рисунок 3.15. К задаче 4
Решение. Пусть заряд конденсатора равен q. (рис.3.15). Тогда электрическая индукция в нём равна D = q/S, а напряжённости электрического поля описываются выражениями:
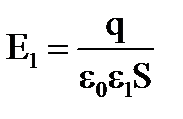 ,
, 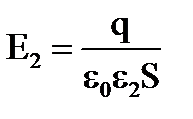 .
.
Разность потенциалов между пластинами равнаU = E1d1 + E2d2. В свою очередь ёмкость конденсатора C= q/U, поэтому:
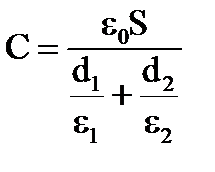
Поляризованность в слоях найдём при помощи формулы:
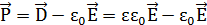 ,
,
а поверхностная плотность связанного заряда 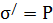 , следовательно
, следовательно
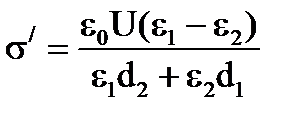 .
.
Ответ: 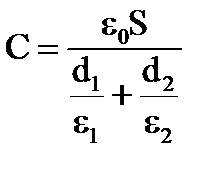 ,
, 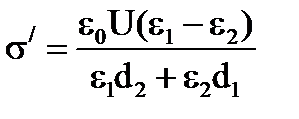 .
.
Задача 5. Плоский конденсатор, площадь каждой пластины которого S=400см2, заполнен двумя слоями диэлектрика. Граница между ними параллельна обкладкам. Первый слой − прессшпан (ε1 = 2) толщины l1=0,2см; второй слой − стекло (ε2 = 7) толщины l2 = 0,3см. Конденсатор заряжен до разности потенциалов U = 600 В. Найти энергию конденсатора.
Решение: Энергию конденсатора можно найти по формуле: 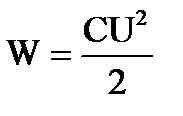 . Определим предварительно электроемкость
. Определим предварительно электроемкость 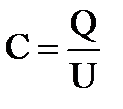 , где Q = σS − заряд конденсатора.
, где Q = σS − заряд конденсатора.
Поскольку в плоском конденсаторе в пределах каждого диэлектрика поле однородно, то U = E1 l1 + E2 l2. Напряжённость поля в каждом слое диэлектрика:
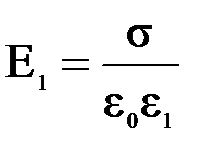 ,
, 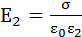
Поэтому
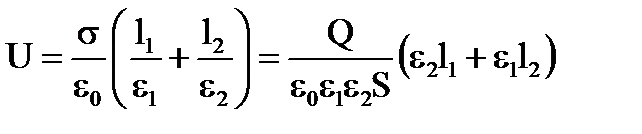 .
.
Тогда электроёмкость конденсатора
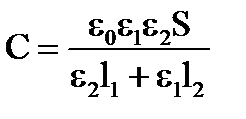 .
.
а энергия конденсатора
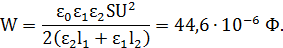
Задача 6. Имеется плоский воздушный конденсатор, площадь каждой обкладки которого равна S. Какую работу против электрических сил надо совершить, чтобы медленно увеличить расстояние между обкладками от х1 до х2, если при этом поддерживать неизменным: а) заряд конденсатора q;
б) напряжение на конденсаторе U?
Решение. а) Вначале энергия конденсатора была равна 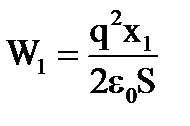 . После увеличения расстояния энергия равна
. После увеличения расстояния энергия равна 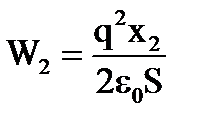 . Совершённая работа равна А = W2 − W1,
. Совершённая работа равна А = W2 − W1, 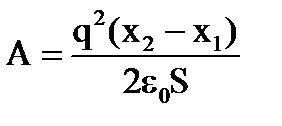
б) Если напряжение на конденсаторе поддерживается постоянным, то при увеличении расстояния между пластинами через источник протекает заряд
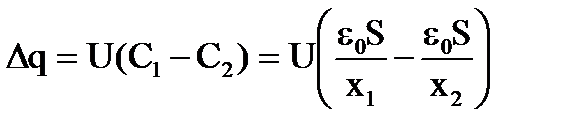 .
.
При этом батарея совершает отрицательную работу A1 = -ΔqU. Поэтому энергетический баланс в этом случае запишется в виде:
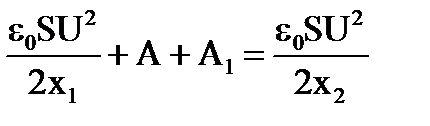 .
.
Решая это уравнение, найдём работу А:
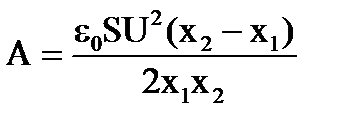 .
.
Выводы:Электроемкость – является важной характеристикой свойств проводников и конденсаторов, характеризующей способность накапливать заряд.
Контрольные вопросы второго уровня (сборник задач)
1. Найти электроемкость С уединенного металлического шара радиусом R=1 см. [1,11 пФ]
2. Определить электроемкость С металлической сферы радиусом R=2 см, погруженной в воду. [180 пФ]
3. Определить электроемкость С Земли, принимая ее за шар радиусом R=6400 км. [712 мкФ]
4. Два металлических шара радиусами R1=2 см и R2=6 см соединены проводником, емкостью которого можно пренебречь. Шарам сообщен заряд q=1 нКл. Найти поверхностную плотность σ зарядов на шарах. [σ1=49,8 нКл/м2; σ2=16,6 нКл/м2]
5. Шар радиусом R1=6 cм заряжен до потенциала φ1=300 В, а шар радиусом R2=4 cм – до потенциала φ2=500 В. Определить потенциал шаров после того, как их соединили металлическим проводником. Емкостью соединительных проводников пренебречь. [380 В]
6. Две концентрические металлические сферы радиусами R1=2 см и R2=2,1 см образуют сферический конденсатор. Определить его электроемкость С, если пространство между сферами заполнено парафином. [93,3 пФ]
7. Металлический шар радиусом 5 см окружен шаровым слоем диэлектрика (ε = 7) толщиной 1 см и помещен концентрично в металлической сфере с внутренним радиусом 7 см. Чему равна емкость такого конденсатора? [0,13 пФ]
8. На одной из пластин плоского конденсатора емкостью С находится заряд +q, а на другой заряд +4q. Определите разность потенциалов между пластинами конденсатора. [3q/(2С)]
9. Два одинаковых плоских воздушных конденсатора емкостью С= 100 пФ каждый соединены в батарею последовательно. Определите, на сколько изменится емкость батареи, если пространство между пластинами одного из конденсаторов заполнить парафином. [Увеличится на 16,7 пФ]
10. Между пластинами плоского конденсатора, площадь которых S, помещен слоистый диэлектрик, состоящий из n слоев вещества с диэлектрической проницаемостью ε1 и из n слоев вещества с диэлектрической проницаемостью ε2. Слои чередуются и каждый имеет толщину d. Найдите емкость конденсатора. [ε0ε1ε2S/dn(ε1+ε2)]
11. Пространство между пластинами плоского конденсатора заполнено диэлектриком, диэлектрическая проницаемость которого линейно меняется от значения ε1 у одной пластины до значения ε2˂ε1 у другой. Расстояние между пластинами d, площадь пластин равна S. Найдите емкость такого конденсатора. [ε0(ε1-ε2)S/d ln(ε1/ε2)]
12. В пространстве между пластинами плоского конденсатора имеется однородный поток электронов, который создает равномерный объемный заряд. Расстояние между пластинами равно d. Потенциал одной из пластин равен φ0. При каком значении объемной плотности заряда ρ потенциал и напряженность поля у другой пластины равны нулю? [ρ=-2ε0φ0/d2]
13. Два конденсатора емкостью С1 = 5 мкФ и С2=8 мкФ соединены последовательно и присоединены к батарее с ЭДС 80 В. Определите заряды q1 и q2конденсаторов и разности потенциалов U1и U2 между их обкладками. [q1 = q2 = 0,246 мКл; U1 = 49 В; U2 = 31 В]
14. Два одинаковых плоских воздушных конденсатора соединены последовательно в батарею, которая подключена к источнику тока с ЭДС 12 В. Определите, на сколько изменится напряжение на одном из конденсаторов, если другой погрузить в трансформаторное масло (ε = 2,2). [2,25 В]
15. Конденсатор емкостью С1 = 0,6 мкФ был заряжен до напряжения U1= 300 В и соединен параллельно со вторым конденсатором емкостью С2 = 0,4 мкФ, заряженным до напряжения U2= 150 В. Найдите величину заряда, перетекшего с пластин первого конденсатора на второй. [36 мкКл]
16. Конденсатор емкостью С, = 0,2 мкФ был заряжен до напряжения U1= 320 В. После того, как его соединили параллельно со вторым конденсатором, заряженным до напряжения U2= 450 В, напряжение на нем изменилось до U = 400 В. Вычислите емкость С2второго конденсатора. [0,32 мкФ]
17. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика: стеклом толщиной d1 = 0,2 см и слоем парафина толщиной d2=0,3 см. Разность потенциалов между обкладками U = 300 В. Определите напряженность Е поля и падение потенциала в каждом из слоев. [E1 = 24 кВ/м; U1= 48 В; Е2= 84 кВ/м; U2= 252 В]
18. Конденсатор емкостью 20 мкФ заряжен до напряжения 400 В. К нему подключается конденсатор емкостью 1 мкФ, в результате чего последний заряжается. Затем, отключив этот конденсатор, заряжают таким же образом второй конденсатор с той же емкостью (1 мкФ), третий и т. д. Затем конденсаторы соединяют последовательно. Какое максимальное напряжение можно получить таким способом? [8 кВ]
19. Плоский конденсатор, пластины которого расположены горизонтально, наполовину залит жидким диэлектриком. Какую часть kаналогичного конденсатора надо залить жидкостью при вертикальном расположении пластин, чтобы емкости в обоих случаях были одинаковы? Диэлектрическая постоянная жидкости ε. [k = 1/(ε + 1)]
20. Четыре одинаковые металлические пластины расположены в воздухе на равных расстояниях dдруг от друга. Площадь каждой из пластин равна S. Крайние пластины соединены между собой, средние пластины подсоединены к батарее, ЭДС которой равна 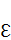 . Найдите заряды средних пластин. Считать, что расстояние dмежду соседними пластинами мало по сравнению с их размерами. [q2 =-q3 = Зε0
. Найдите заряды средних пластин. Считать, что расстояние dмежду соседними пластинами мало по сравнению с их размерами. [q2 =-q3 = Зε0 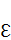 S/2d]
S/2d]
21. У расположенного горизонтально незаряженного плоского конденсатора нижняя пластина закреплена, а верхняя подвешена к коромыслу весов. Весы находятся в равновесии, при расстоянии между пластинами d= 1 мм. Какой массы грузик надо положить на вторую чашку весов, чтобы сохранить равновесие при том же расстоянии между пластинами, если конденсатор зарядить до напряжения U=1000 В? Площадь пластин конденсатора S= 50 см2. [2,25 г]
22. Одна пластина конденсатора закреплена неподвижно, вторая подвешена к пружине с коэффициентом жесткости k. Площадь пластин S. На сколько удлинится пружина, если пластинам сообщить равные, но противоположные по знаку заряды q? Поле между пластинами считать однородным. [Δl=q2/2ε0kS]
23. Одна пластина конденсатора закреплена неподвижно на дне широкого сосуда с жидким диэлектриком (диэлектрическая проницаемость его ε, плотность ρ). Вторая, имеющая вид бруска высотой H, плавает над ней, погрузившись на 1/4 своего объема, если пластины не заряжены. Какую разность потенциалов надо приложить к пластинам, чтобы верхняя пластина погрузилась наполовину? Первоначальное расстояние между пластинами конденсатора H. Поле между пластинами считать однородным. [ 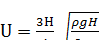 ]
]
24. Плоский воздушный конденсатор с площадью пластины S= 5 см2 подключен к батарее, ЭДС которой 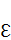 = 300 В. Определите работу внешних сил по раздвижению пластин от d1 = 1 мм до d2 - 3 мм если перед раздвижением пластины отключаются от батареи. [0,4 мкДж]
= 300 В. Определите работу внешних сил по раздвижению пластин от d1 = 1 мм до d2 - 3 мм если перед раздвижением пластины отключаются от батареи. [0,4 мкДж]
25. Плоский воздушный конденсатор с площадью пластины S= 5 см2 подключен к батарее, ЭДС которой 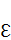 = 300 В. Определите работу внешних сил по раздвижению пластин от d1=- 1 мм до d2 = 3 мм, если пластины в процессе раздвижения остаются подключенными к батарее. [-0,13 мкДж]
= 300 В. Определите работу внешних сил по раздвижению пластин от d1=- 1 мм до d2 = 3 мм, если пластины в процессе раздвижения остаются подключенными к батарее. [-0,13 мкДж]
26. Металлический шар радиусом R= 2 см несет заряд q=30 нКл. Шар окружен слоем парафина толщиной d= 3 см. Определите энергию электрического поля, заключенного в слое диэлектрика. [0,18 мДж]
27. Плоский конденсатор находится во внешнем однородном электрическом поле с напряженностью Е, направление которого совпадает с направлением поля в конденсаторе. По пластинам равномерно распределены заряды q и -q. Какую работу надо совершить, чтобы перевернуть конденсатор, поменяв пластины местами? Расстояние между пластинами d. Влиянием силы тяжести пренебречь. [А = 2qdE]
28. Большая тонкая проводящая пластина, площадь которой равна S, а толщина d, помещена в однородное электрическое поле с напряженностью Е, перпендикулярное пластине. Какое количество теплоты выделится в проводнике, если поле мгновенно выключить? [Q = 0,5ε0dE2S]
29. Два плоских конденсатора емкостью Скаждый, соединенные параллельно и заряженные до напряжения U, отсоединяют от источника. Пластины одного из конденсаторов могут двигаться свободно навстречу друг другу. Найдите их скорость в момент, когда зазор между пластинами конденсатора уменьшится в два раза. Масса каждой пластины равна М. Силой тяжести пренебречь .[v=U 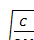 ]
]
30. Два металлических шарика радиусами R1 = 5 см и R2= 10 см имеют заряды q1 = 40 нКл и q2=-20 нКл соответственно. Найдите энергию, которая выделится при разряде, если шары соединить проводником. [0,15 мДж]
Контрольные вопросы третьего уровня (тесты)
1. Какое из приведенных ниже выражений есть определение электроемкости конденсатора?
| а)C = 4pe0eR; | б) С = ; | в)С = ; |
| г) С = ; | д)С = . |
2. От каких факторов зависит емкость уединенного проводника, расположенного в вакууме?
а) только от размеров проводника;
б) только от формы проводника;
в) от формы и размеров проводника;
г) от формы, размеров и материала проводника;
д) от формы, размеров и от заряда проводника.
3. Энергия заряженного проводника определяется выражением:
| а); | б) ; | в) ; | г). |
4. Энергия электрического поля определяется выражением:
| а); | б) ; | в) ; | г). |
5. Электроемкости конденсатора поставьте в соответствие математическое выражение.
| Электроемкость | Математическое выражение | ||
| а) электроемкость плоского конденсатора | 1) | ||
| б) электроемкость сферического конденсатора | 2) | ||
| в) электроемкость цилиндрического конденсатора | 3) | ||
| а) ; | б) ; | в) . | |
6. Какое из приведенных ниже выражений есть определение плотности энергии электрического поля?
| а); | б) rE = ; | в) rE = ; | г) rE = . |
7. Определить разность потенциалов между обкладками первого конденсатора, если разность потенциалов между обкладками третьего конденсатора равна U.
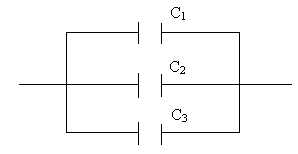
1. U 2. 3U 3. U/3 4. 0 5. 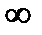
8. Определить заряд первого конденсатора, если заряд третьего равен 3q?
1. q 2. 2q 3. 3q 4. 0 5. q/3 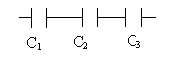
9. Как изменится емкость конденсатора, если у него изъять диэлектрик с диэлектрической проницаемостью e?
1)Уменьшится в e раз. 2)Увеличится в e раз. 3) Останется прежней.
4) Станет равной нулю.
10. Чему равна емкость изображенной батареи конденсаторов?
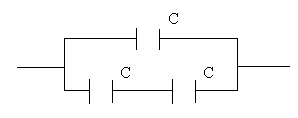
1) 0.5С 2) С 3) 2С 4) 1.5С 5) 2.5С
Дата добавления: 2015-02-13; просмотров: 42865;
