Механические гармонические колебания

Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат xоколо положения равновесия, принятого за начало координат. Тогда зависимость координаты хот времени tзадается уравнением, аналогичным уравнению (140.1), где s = х:

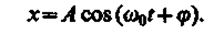(141.1)

Согласно выражениям (140.4) и (140.5), скорость v и ускорение а колеблющейся точки соответственно равны

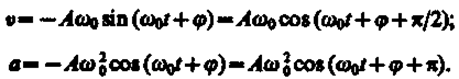(141.2)

Сила F = ma, действующая на колеблющуюся материальную точку массой т, с учетом (141.1) и (141.2) равна

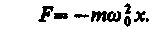
Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия).

Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна

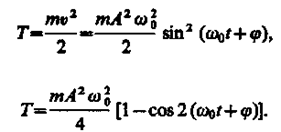(141.3) (141.4)

Потенциальная энергии материальной точки, совершающей гармонические колебания под действием упругой силы F, равна

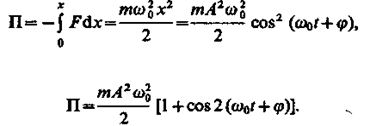(141.5) (141.6)

Сложив (141.3) и (141.5), получим формулу для полной энергии:

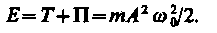(141.7)

Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения механической энергии, поскольку упругая сила консервативна. Из формул (141.4) и (141.6) следует, что Т и П изменяются с частотой 2w₀,т. е. с частотой, которая в два раза превышает частоту гармонического колебания. На рис. 200 представлены графики зависимости х, Т и П от времени. Так как ásin²añ = ácos² añ = 1/2, то из формул (141.3), (141.5) и (141.7) следует, что áТñ = áПñ = 1/2Е.

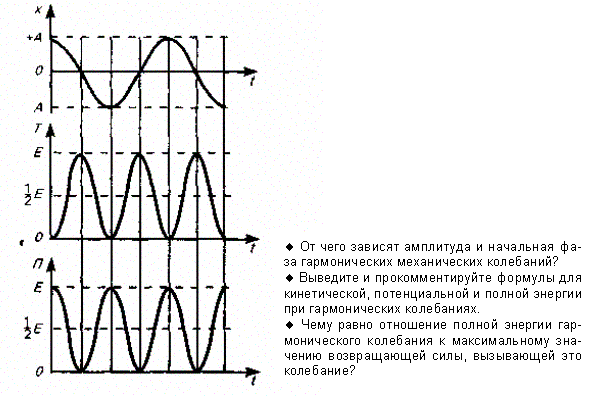
Рис. 200