Деформации твердого тела
Рассматривая механику твердого тела, мы пользовались понятием абсолютно твердого тела. Однако в природе абсолютно твердых тел нет, так как все реальные тела под действием сил изменяют свою форму и размеры, т. е. деформируются.
Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются пластическими (или остаточными). Деформации реального тела всегда пластические, так как они после прекращения действия внешних сил никогда полностью не исчезают. Однако если остаточные деформации малы, то ими можно пренебречь и рассматривать упругие деформации, что мы и будем делать.
В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходящим деформациям растяжения или сжатия и сдвига.
Рассмотрим однородный стержень длиной / и площадью поперечного сечения S (рис. 34), к концам которого приложены направленные вдоль его оси силы F1 и F2 (F1 = F2 = F),в результате чего длина стержня меняется на величину Dl.
Естественно, что при растяжении Dl положительно, а при сжатии отрицательно.
Сила, действующая на единицу площади поперечного сечения, называется напряжением:
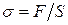 (21.1)
(21.1)
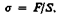
|
Если сила направлена по нормали к поверхности, напряжение называется нормальным, если же по касательной к поверхности — тангенциальным.
Количественной мерой, характеризующей степень деформации, испытываемой те лом, является его относительная деформация. Так, относительное изменение длины стержня (продольная деформация)
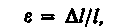 (21.2)
(21.2)
относительное поперечное растяжение (сжатие)
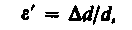
где d — диаметр стержня.
Деформации e и e¢всегда имеют разные знаки (при растяжении Dl положительно, a Dd отрицательно, при сжатии Dl отрицательно, а Dd положительно). Из опыта вытекает взаимосвязь e и e¢:

где m— положительный коэффициент, зависящий от свойств материала и называемый коэффициентом Пуассона *.
Английский физик Р. Гук (1635—1703) экспериментально установил, что для малых деформаций относительное удлинение е и напряжение а прямо пропорциональны друг другу:
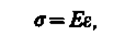 (21.3)
(21.3)
где коэффициент пропорциональности Е называется модулем Юнга**. Из выражения (21.3) видно, что модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице.
Из формул (21.2), (21.3) и (21.1) вытекает, что

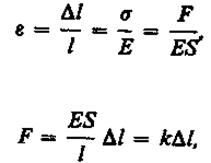 (21.4)
(21.4)
где k — коэффициент упругости. Выражение (21.4) также задает закон Гука, согласно которому удлинение стержня при упругой деформации пропорционально действующей на стержень силе.
Деформации твердых тел подчиняются закону Гука до известного предела. Связь между деформацией и напряжением представляется в виде диаграммы напряжений, качественный ход которой мы рассмотрим для металлического образца (рис. 35). Из рисунка видно, что линейная зависимость s(e), установленная Гуком, выполняется лишь в очень узких пределах до так называемого предела пропорциональности (sп). При дальнейшем увеличении напряжения деформация еще упругая (хотя зависимость s(e) уже нелинейна) и до предела упругоcти (sу) остаточные деформации не возникают. За пределом упругости в теле возникают остаточные деформации и график, описывающий возвращение тела в первоначальное состояние после прекращения действия силы, изобразится не кривой ВО, а параллельной ей — CF. Напряжение, при котором появляется заметная остаточная деформация («0,2%), называется пределом текучести (sт) — точка С на кривой. В области CD деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область текучести значительна, называются вязкими, для которых же она практически отсутствует — хрупкими. При дальнейшем растяжении (за точку D) происходит разрушение тела. Максимальное напряжение, возникающее в теле до разрушения, называется пределом прочности (sp).
Диаграмма напряжений для реальных твердых тел зависит от различных факторов. Одно и то же твердое тело может при кратковременном действии сил проявлять себя как хрупкое, а при длительных, но слабых силах является текучим.
Вычислим потенциальную энергию упругорастянутого (сжатого) стержня, которая равна работе, совершаемой внешними силами при деформации:
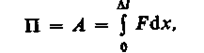
где х — абсолютное удлинение стержня, изменяющееся в процессе деформации от 0 до Dl. Согласно закону Гука (21.4), F = kx = ESx/l. Поэтому
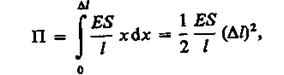
т. е. потенциальная энергия упругорастянутого стержня пропорциональна квадрату деформации (Dl)2.
Деформацию сдвига проще всего осуществить, если взять брусок, имеющий форму прямоугольного параллелепипеда, и приложить к нему силу Ft (рис. 36), касательную к его поверхности (нижняя часть бруска закреплена неподвижно). Относительная деформация сдвига определяется из формулы
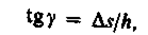
где Ds – абсолютный сдвиг параллельных слоев тела относительно друг друга; h – расстояние между слоями (для малых углов tgg » g).
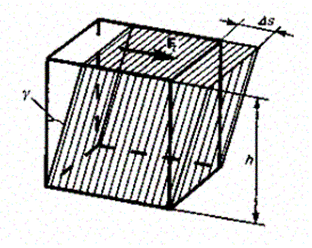
Рис. 36
Задачи
4.1. С одного уровня наклонной плоскости одновременно начинают скатываться без скольжения сплошные цилиндр и шар одинаковых масс и одинаковых радиусов. Определить: 1) отношение скоростей цилиндра и шара на данном уровне; 2) их отношение в данный момент времени. [1) 14/15; 2) 14/15]
4.2. К ободу однородного сплошного диска радиусом R=0,5 м приложена постоянная касательная сила F= 100 Н. При вращении диска на него действует момент сил трения М=2Н×м. Определить массу т диска, если известно, что его угловое ускорение e постоянно и равно 12 рад/с2. [32 кг]
4.3. Через неподвижный блок в виде однородного сплошного цилиндра массой m = 1кг перекинута невесомая нить, к концам которой прикреплены тела массами m1 = 1кг и m2 = 2 кг. Пренебрегая трением в оси блока, определить: 1) ускорение грузов; 2) отношения T2/T1сил натяжения нити. [1) 2,8 м/с2; 2) 1,11]
4.4. Скорость вращения колеса, момент инерции которого 2 кг×м2, вращающегося при торможении равнозамедленно, за время t=1 мин уменьшилась от n1 = 300 мин-1 до n2=180 мин-1. Определить: 1) угловое ускорение е колеса; 2) момент М силы торможения; 3) работу силы торможения. [1) 0.21 рад/с2; 2) 0,42 Н-м; 3) 630 Дж]
4.5.Человек массой m = 80 кг, стоящbй на краю горизонтальной платформы массой M = 100 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n1 = 10 мин-1, переходит к ее центру. Считая платформу круглым однородным диском, а человека — точечной массой, определить, с какой частотой n2 будет тогда вращаться платформа. [26 мин-1]
4.6. Определить относительное удлинение алюминиевого стержня, если при его растяжении затрачена работа 62,1 Дж. Длина стержня 2 м, площадь поперечного сечения 1 мм2, модуль Юнга для алюминия E = 69 ГПа. [ 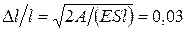 ]
]
Дата добавления: 2015-02-13; просмотров: 1551;
