Уравнение движения поезда.

Движение поезда происходит под действием рассмотренных выше сил.

– силы тяги F_К;

– силы сопротивления движению W_К;

– тормозной силы В_Т.

Алгебраическая сумма этих сил определяет равнодействующую силу

,

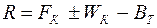по которой можно судить о характере движения поезда. Уравнение описывающее зависимость между ускорением и равнодействующей приложенных к поезду сил называется уравнением движения поезда.

Рассмотрим движение поезда как движение массы, сконцентрированной в одной точке – центре тяжести и применим второй закон Ньютона:

“Модуль силы, действующей на материальную точку, равен произведению массы на модуль ее ускорения, а направление силы совпадает с направлением ускорения”.

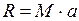, откуда ,

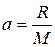где R – равнодействующая приложенных сил , Н;

М – масса поезда, кг;

а – ускорение поезда, м/с².

Масса поезда может быть выражена через его вес и ускорение свободного падения, т.е. силы тяжести.

,

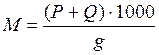где 1000 – коэффициент для перевода тонн в кг;

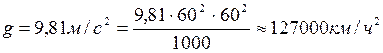
Подставляя в формулу массы, получим:

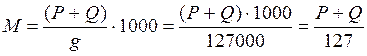, Н·ч²/км.

Выразив ускорение поезда через 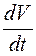и подставив значения R и М получаем уравнение движения поезда:

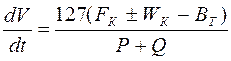, Н·км/Н·ч²=км/ч²

или через удельные силы, действующие на поезд:

.

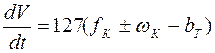Из уравнения следует, что удельная сила создает ускорение поезда, равное 127 км/ч² на 1 Н/кН.

В действительности ускорение поезда несколько меньше, чем дает выведенное уравнение, т.к. силы, действующие на поезд затрачиваются не только на создание поступательного ускорения, но и на создание вращающего из уравнения следует, что удельная сила создает ускорение поезда ускорения колес и т.д. Поэтому для общих расчетов принимается формула:

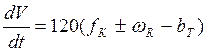, км/ч².