Продольной компенсации
Напряжение у потребителей зависит от величины потерь напряжения в сети. Потери напряжения зависят от сопротивления сети. Потеря напряжения на участке сети, рассчитанная при заданном напряжении в конце, равна
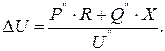 (20.1)
(20.1)
Соотношение активного и индуктивного сопротивлений в распределительных и питающих сетях различно. Это наглядно видно на рис. 20.4.

В распределительных сетях активное сопротивление больше ин-дуктивного. В потере напряжения основную роль играет составляющая 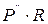 . В питающей сети индуктивное сопротивление больше активного. Потеря напряжения в значительной степени определяется реактивным сопротивлением участка сети.
. В питающей сети индуктивное сопротивление больше активного. Потеря напряжения в значительной степени определяется реактивным сопротивлением участка сети.
Изменение индуктивного сопротивления применяют для регулирования напряжения. Чтобы изменить индуктивное сопротивление, необходимо включить в линию электропередач батарею конденсаторов. Возможность регулирования напряжения при помощи устройства продольной компенсации покажем для простейшего участка сети (рис. 20.5). Потеря напряжения на участке определяется выражением (20.1). Допустим, что напряжение в конце участка ниже допустимого:
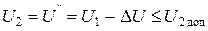 .
.
 Включим последовательно в линию электропередач батарею конденсаторов так, чтобы повысить напряжение до допустимой величины
Включим последовательно в линию электропередач батарею конденсаторов так, чтобы повысить напряжение до допустимой величины 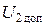 . Напряжение в конце участка сети будет равно:
. Напряжение в конце участка сети будет равно:
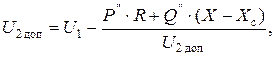
где Хс – сопротивление батареи конденсаторов.
Запишем это выражение через ток, который протекает в линии электропередач:
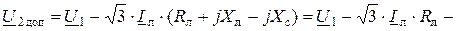
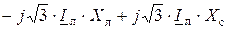 (20.2)
(20.2)
Используем полученное выражение для построения векторной диаграммы регулирования напряжения при помощи устройства продольной компенсации.
 |
Из начала координат по действительной оси отложим вектор напряжения U1. Получим точку а. Под углом φ2 к нему отложим ток на участке Iл. Вектор падения напряжения в активном сопротивлении параллельно линии тока отложим от конца вектора напряжения U1 с учетом знака в выражении (20.2). Получим точку b. Из точки b перпендикулярно линии тока отложим вектор падения напряжения в индуктивном сопротивлении ЛЭП с учетом знака в выражении (20.2). Получим точку с. Соединим начало координат с точкой с. Полученный вектор – это вектор напряжения в конце участка. Его величина меньше допустимого значения напряжения 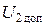 . Из точки с перпендикулярно линии тока отложим вектор падения напряжения в сопротивлении батареи конденсаторов с учетом знака в выражении (20.2). Получим точку d. Соединив точку d с началом координат, получим вектор напряжения в конце участка
. Из точки с перпендикулярно линии тока отложим вектор падения напряжения в сопротивлении батареи конденсаторов с учетом знака в выражении (20.2). Получим точку d. Соединив точку d с началом координат, получим вектор напряжения в конце участка 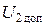 . Его величина удовлетворяет требованиям.
. Его величина удовлетворяет требованиям.
Величину 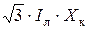 можно рассматривать как отрицательное падение напряжения или как дополнительную ЭДС.
можно рассматривать как отрицательное падение напряжения или как дополнительную ЭДС.
Из выражения для 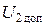 можно определить сопротивление батареи конденсаторов. По его величине определить количество последовательных и параллельно включенных конденсаторов. При этом напряжение на батарее конденсаторов Uк и ток Iк в ней равны
можно определить сопротивление батареи конденсаторов. По его величине определить количество последовательных и параллельно включенных конденсаторов. При этом напряжение на батарее конденсаторов Uк и ток Iк в ней равны
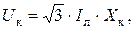
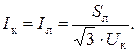
Если номинальное напряжение одного конденсатора меньше фазного напряжения в месте установки батареи конденсаторов 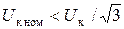 , то в фазе ставятся последовательно несколько конденсаторов. Их количество n определяется по выражению
, то в фазе ставятся последовательно несколько конденсаторов. Их количество n определяется по выражению
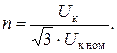
В паспорте конденсатора указывается его номинальная мощность Qк. Зная эту величину, можно определить номинальный ток конденсатора Iк ном:
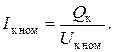
Если номинальный ток конденсатора меньше тока в ЛЭП 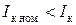 , то ставят параллельно m конденсаторов:
, то ставят параллельно m конденсаторов:
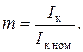
Отношение
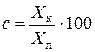
называется процентом компенсации. На практике применяют частичную компенсацию (с < 100 %) индуктивного сопротивления ЛЭП. Полная компенсация не применяется, так как это связано с возможностью появления перенапряжений в сети.
Применение УПК позволяет улучшить режимы напряжения в сети. Повышение напряжения зависит от значения и фазы тока, которых проходит через УПК. Поэтому возможности регулирования напряжения через УПК ограничены. Наиболее эффективно применение УПК для снижения отклонений напряжения на перегруженных радиальных ЛЭП.
Дата добавления: 2015-02-13; просмотров: 696;
