Основы рисунка
Перед тем как использовать программу-функцию нужно ее описать. Описание программы-функции размещается в рабочем документе перед вызовом программы-функции и включает в себя заголовок функции и тело функции, соединенные в единое целое с помощью операции присваивания («:=»).
Заметим, что если программа используется для вычисления одного значения, то в своем заголовке она не содержит списка формальных параметров и называется программой-скаляром.
Программа-функция может не иметь формальных параметров и тогда, когда данные передаются через имена переменных, определенных выше описания программы-функции. Эти переменные будут являться глобальными для данной функции.
Технология создания программы-функции в рабочем документе MathCAD состоит из следующих шагов:
Ввести заголовок функции.
Ввести знак присваивания «:=».
Выполнить команду Add line, расположенную на панели Programming (Программирование). Появившейся на экране шаблон с вертикальной чертой и полями для ввода операторов будут составлять заготовку для тела программы-функции.
Вписать операторы в шаблон-заготовку. Тело программы-функции может включать любое число операторов: локальных операторов присваивания, условных операторов и операторов цикла, а также вызов других программ-функций.
Самое нижнее поле всегда предназначено для определения возвращаемого программой значения.
Пример 1. Требуется подготовить описание функции 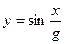 и вычислить значения этой функции при x = 4.15 и g = 1.854.
и вычислить значения этой функции при x = 4.15 и g = 1.854.
Решение. Заметим, что при вычислении y можно обойтись без описания и использования пользовательской функции и тем более без программирования, как это показано на рис. 8.4, a. Использование функции следует из требования к задаче для простоты изложения. Для нахождения значения функции «внутрь» программы-функции следует передать значения x и g, необходимые для выполнения вычислений внутри программы. Поэтому переменные x и g следует включить в список формальных параметров заголовка создаваемой функции. Назовем эту функцию – y. Тогда подготовка описания функции, и ее выполнение в соответствии с описанной технологией могут быть выполнены, как это представлено на рис. 8.3.
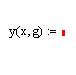 (1-2)
(1-2)
|
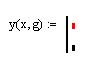 (3)
(3)
| 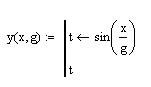 (4-5)
(4-5)
|
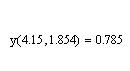 (6)
(6)
|
Рис.7.3. Пошаговое создание и выполнение программы-функции
В данном примере введена вспомогательная локальная переменная t для вычисления значения функции. И эта переменная расположена в последней строчке программного блока. В пункте (6) приведена операция вычисления функции для фактических значений. На рис. 8.4, b, c приведены другие варианты решения поставленной задачи.
| a) | b) | c) |
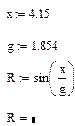
|
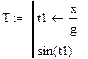
|
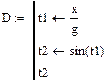
|
Рис. 8.4. Демонстрация элементов программирования простых выражений
В примере, представленном на рис. 8.4, в первой колонке a для вычисления значения 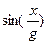 используется базовый набор средств без элементов программирования. Во второй b и третьей c колонках производятся точно такие же вычисления, но с использованием элементов программирования. Обе программы (b и c) можно считать эквивалентными, так как возвращают они одно и то же значение, которое располагается в последней строчке программируемой части. В (b и c) мы имеем дело с программой – скаляром, так как они используются для вычисления одного значения и не имеют формальных параметров.
используется базовый набор средств без элементов программирования. Во второй b и третьей c колонках производятся точно такие же вычисления, но с использованием элементов программирования. Обе программы (b и c) можно считать эквивалентными, так как возвращают они одно и то же значение, которое располагается в последней строчке программируемой части. В (b и c) мы имеем дело с программой – скаляром, так как они используются для вычисления одного значения и не имеют формальных параметров.
Внутри программ (b и c) используются глобальные переменные g и x из документа. Значения этих переменных определены заранее. Обе программы из примера, представленного на рис. 8.4, в своей программируемой части содержат операторы присваивания с использованием локальных переменных. Переменные, созданные внутри программы с таким видом присваивания, являются внутренними, и доступ к ним может осуществляться только в самой программе.
 В программной части используются глобальные переменные обычно только как операнды в выражениях.
В программной части используются глобальные переменные обычно только как операнды в выражениях.
Присвоить глобальным переменным значения внутри программы можно только локальным образом. После выхода из программы эти переменные сохраняют свои «глобальные» значения.
Использование «обычного» оператора присваивания «:=» в теле программы-функции приводит к синтаксической ошибке.
Последняя строка программы не должна содержать управляющих операторов. Эта строка задает значение, возвращаемое программой, т.е. получает результат вычислений и может содержать имя локальной переменной результата (рис. 8.4, c) или выражение, вычисляющее результат (рис. 8.4, b).
Обычно программа содержит больше чем две строки, поэтому рекомендуется сразу задавать блок из 5-6 маркеров.
Добавление недостающих полей для ввода дополнительных операторов производится с помощью кнопки Add line панели программирования. При этом поле ввода добавляется внизу выделенного к этому моменту оператора.
Для удаления того или иного оператора или поля ввода из тела программы-функции, нужно заключить его выделить и нажать клавишу <Delete> .
Программный блок можно создать и внутри уже заданного блока (вложенный блок). Для этого следует использовать один из стандартных способов: поставить курсор в маркер соответствующего оператора программирования и выполнить Add line.
Иногда при написании программы бывает нужным добавить строку к уже созданному блоку. Чтобы это сделать, поставьте курсор в ту строку блока, выше или ниже которой должна быть введена строка, и нажмите клавишу <Пробел>. При этом строка будет выделена и можно будет произвести добавление одним из стандартных способов.
Положение вставляемого маркера определяется положением вертикальной черты курсора. Если она находится слева от выделенного выражения, то маркер будет добавлен выше выделенной строки, если справа – то ниже.
Чтобы развернуть курсор в нужную сторону, нажмите клавишу <Insert>.
Чтобы добавить строку к целому блоку, его следует выделить, дважды нажав клавишу <Пробел>.
В том случае, если программа содержит блоки различных уровней, то для добавления строки, например, к первому блоку, нажмите клавишу <Пробел> несколько раз: при каждом нажатии будут выделяться блоки более низкого уровня.
Пример 2. Требуется найти действительные корни квадратного уравнения 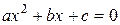 , где a, b, c – любые действительные числа и
, где a, b, c – любые действительные числа и 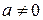 . Известно, что в зависимости от знака дискриминанта
. Известно, что в зависимости от знака дискриминанта 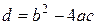 действительные корни уравнения могут быть получены по формуле:
действительные корни уравнения могут быть получены по формуле:
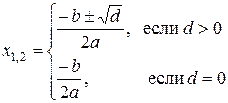
Блок-схема этого алгоритма показана в главе 1 на рис. 1.2.
Решение. Опишем вычисление корней в виде программы-функции. Спецификацию для этой функцииможно записать следующим образом. Функция R(a,b,с) возвращает значения действительных корней квадратного уравнения 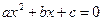 или сообщает о том, что уравнение не имеет корней. Здесь a, b, с – коэффициенты уравнения.
или сообщает о том, что уравнение не имеет корней. Здесь a, b, с – коэффициенты уравнения.
Очевидно, что в данном случае мы имеем дело с ветвящимся процессом. Программирование ветвящихся процессов требует проверки некоторых условий, в зависимости от которых выбирается вычислительная формула. Для реализации таких вычислений на панели программирования предусмотрен оператор if(если).

При включении оператора ifв блок программирования появляется шаблон с двумя полями ввода – справа и слева от оператора:
g ifg.
В поле ввода справа от оператора записывается условие. Для ввода условий следует использовать панель Boolean(Логические), где есть кнопки для проверки условий ( = > < ≥ ≤ ≠ ).
В поле ввода слева нужно ввести строку программы (или несколько строк), которая будет выполняться, если введенное условие истинно.
Если невыполнение условия должно привести к выполнению какой-либо другой строки (или нескольких строк), то можно в строке, следующей за оператором if , вставить оператор otherwise
(иначе). В поле ввода слева от этого оператора надо ввести строку, которая будет выполняться только в том случае, если условие ложно.
Чаще всего оператор if используется для задания разрывных или кусочно-непрерывных функций.
Описание функции и примеры ее вызова представлены на рис. 8.5.

Рис. 8.5. Описание функции R(a,b,x), предназначенной для вычисления
корней квадратного уравнения
Пример 3. Требуется подготовить описание программы-функции 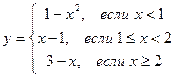 и построить ее график на интервале [–2, 4] .
и построить ее график на интервале [–2, 4] .
Решение. Из анализа аналитического выражения функции y видно, что функция является кусочно-непрерывной на числовой оси и алгоритм вычислений содержит три ветви. Вычисление значения y зависит от местоположения переменной x на числовой оси.
Для нахождения значения функции целесообразно ввести один формальный параметр, соответствующий переменной x. Спецификацию для этой функцииможно записать следующим образом:
Функция f(x) возвращает значение функции, определенной в соответствии с условием примера 3. Здесь х – аргумент для вычисления.
В описании функции требуется проверить три условия. В зависимости от результатов проверки этих условий применяется соответствующая условию вычислительная формула. Поэтому при программировании можно с проверкой каждого из условий связать условный оператор if, как это показано на рис. 8.6. А можно ограничиться проверкой двух условий и оператором otherwise, учитывая тот факт, что функция задана на всей числовой оси, и исключение двух условий оставляет выполнение третьего условия. На рис. 8.7 представлен второй вариант функции-программы.
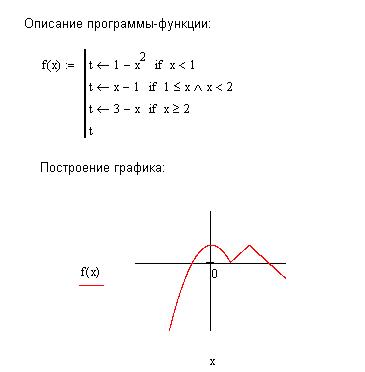
Рис. 8.6. Демонстрация элементов программирования ветвящихся процессов
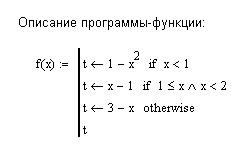
Рис. 8.7. Демонстрация элементов программирования ветвящихся процессов
На рис. 8.8 представлены примеры программ-функций, реализующих вычисления, содержащие ветвящиеся процессы.
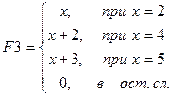
| 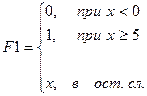
|
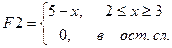
|
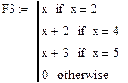
|
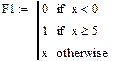
|
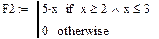
|
Рис. 8.8. Примеры программирования функций с проверкой условий. Здесь x – глобальная переменная
Пример 4. Требуется найти максимальный и минимальный элементы в заданном массиве.
Решение. Задача поиска наибольшего/наименьшего значений в заданном массиве относится к типовым циклическим алгоритмам и подробно описана в главе 1, а на рис.1.9 и 1.10 приведены блок-схемы этих алгоритмов.
Спецификацию для этой функцииможно записать следующим образом:
Функция Fun(P) возвращает наибольшее и наименьшее значение в массиве Р.
Для создания циклов в MathCAD предусмотрено два оператора: for и while. Поскольку количество повторений цикла заранее известно и связано с числом элементов заданного массива, в данном решении целесообразно использовать оператор for.
 После вставки оператора for в строку программы его сопровождают три поля ввода, как это показано на рис. 8.9.
После вставки оператора for в строку программы его сопровождают три поля ввода, как это показано на рис. 8.9.
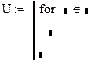
Рис. 8.9. Шаблон оператора цикла for
В поле ввода после слова forследует указать имя переменной-счетчика. Это может быть любое имя, которое не использовалось ранее в программе. Внутри цикла можно использовать эту переменную в любых выражениях, нельзя только присваивать ей никакого значения.
В поле ввода после знака €следует указать диапазон значений, которые будет принимать переменная-счетчик. Вместо диапазона в данном поле ввода можно указать имя некоторого массива (вектора или матрицы). В таком случае переменная-счетчик будет последовательно принимать значения всех элементов этого массива. Количество повторов цикла будет равно количеству элементов массива.
В поле ввода под словом forследует ввести тело цикла
Обозначим имя переменной-счетчика, которая используется в оператореfor – буквой t. Для описания алгоритма воспользуемся тем, что в операторе цикла для переменной-счетчика можно указать в качестве диапазона имя массива. Как сказано выше, в таком случае переменнаяt будет последовательно принимать значения всех элементов указанного в for массива (в нашем случае – это массив Р). Для обозначения максимального и минимального значений в программу введем две вспомогательные переменные Pmax и PMin. Тогда описание функции может быть представлено в виде, как это показано на рис. 8.10.
Отметим, что в данном случае в качестве результата работы функции нужно вернуть два значения, а специфика функции в MathCAD такова, что она позволяет вернуть только одно значение, но при этом сказано, что функция в качестве результата может вернуть, в том числе, вектор и матрицу. Поэтому при формировании результата мы определим его как вектор из двух значений.
Справа от программы-функции, представленной на рис. 8.10, написаны операторы, предназначенные для создания вектора с именем U из шести элементов. Для этого введена вспомогательная переменная i, задающая диапазон изменения индекса массива, а значения элементов массива U формируются с помощью функции rnd – датчика случайных чисел. Параметр 20 в ней определяет диапазон принимаемых значений.
На рис. 8.11, a представлен второй вариант программы-функции, в котором в качестве диапазона значений для переменной-счетчика цикла for берется диапазон изменения индекса массива. Поэтому в список формальных параметров в заголовок функции вносится еще один параметр n, который указывает верхнюю границу изменения индекса.

Рис. 8.10. Описание и использование функции Fun(P)
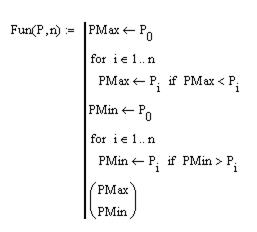 а)
а)
|  b)
b)
|
Рис. 8.11. Описание и использование функции Fun(P)
Пример 5. Требуется определить функцию, предназначенную для вычисления приближенного значения квадратного корня из числа N по формуле Ньютона:
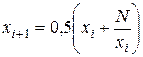
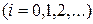 ,
,
где 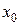 - заданное начальное приближение корня.
- заданное начальное приближение корня.
Решение. Алгоритм решения задача подробно рассмотрен в главе 1, блок-схема алгоритма представлена на рис. 1.5. Поэтому остановимся только на спецификации программы-функции, и ее описании. Спецификацию для этой функцииможно записать следующим образом:
Функция Fun(N,e,x0) возвращает значение квадратного корня из числа N с заданной точностью вычислением – e и заданным начальным приближением корня – x0.
Анализ блок-схемы показывает, что в представленном циклическом процессе количество повторений цикла заранее неизвестно и напрямую зависит от точности вычислений. Поэтому пользоваться оператором for не является целесообразным. Для таких циклических процессов предусмотрен оператор цикла while.
 После вставки этого оператора в строку программы его сопровождают два поля ввода, как это показано на рис. 8.12.
После вставки этого оператора в строку программы его сопровождают два поля ввода, как это показано на рис. 8.12.
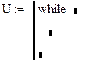
Рис. 8.12. Шаблон оператора цикла while
В поле ввода ниже слова while следует ввести тело цикла – одна или несколько строк программы, выполнение которых нужно повторить несколько раз.
В поле ввода справа от слова while следует ввести условие. Оно будет проверяться после каждого выполнения тела цикла и в тот момент, когда условие перестанет выполняться, повторение тела цикла прекратится.
Из описания оператора цикла следует, что условие повторения цикла записывается cправа от слова while, а повторяемая часть цикла должна располагаться ниже конструкции while, а в описанной блок-схеме один из повторяемых операторов, а именно оператор, в котором вычисляется значение х, располагается до блока с условием повторения. Чтобы согласовать действия в блок-схеме с действиями оператора, сделаем перестановку — поставим определение переменной х после блока-условия. А для проверки условия введем вспомогательную переменную R, и для того, чтобы на начальном этапе пройти внутрь цикла для вычислений, определим начальное значение этой переменной значением, большим, чем указанная точность, например, значением, равным 1. И тогда функция может быть представлена в виде, как это показано на рис. 8.13.
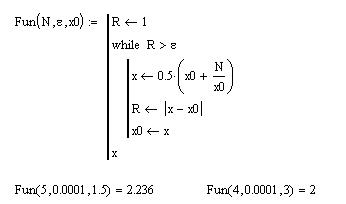
Рис. 8.13. Описание и использование функции,
предназначенной для извлечения квадратного корня
Пример 6. Требуется определить функцию, которая будет изменять значения элементов матрицы 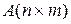 , имеющей n строк и m столбцов следующим образом: заменить все неотрицательные элементы нулем, а отрицательные – единицей.
, имеющей n строк и m столбцов следующим образом: заменить все неотрицательные элементы нулем, а отрицательные – единицей.
Решение. Алгоритм решения задача подробно рассмотрен в главе 1, блок-схема алгоритма представлена на рис. 1.11. Поэтому остановимся только на спецификации программы-функции, и ее описании. Спецификацию для этой функцииможно записать следующим образом:
Функция Fun(а,n,m) возвращает преобразованную матрицу а(nxm) по правилу: все неотрицательные элементы заменяются нулем, а отрицательные – единицей.
Анализ алгоритма показывает, что в данном случае мы имеем дело с двумя вложенными циклами, в которых переменные iи jмогут играть роль переменных-счетчиков операторов цикла типа for. Очевидно, что в качестве диапазона значений для этих переменных берется диапазон изменения индекса массива. На рис. 8.14 приведено определение функции. Описанная функция вызывается для изменения матрицы D, причем, измененная матрица заносится в матрицу T.

Рис. 8.14. Описание и использование функции, предназначенной
для преобразования матрицы
 Подготовить спецификацию функции.
Подготовить спецификацию функции.
Разработать алгоритм решения.
Установить, какие переменные помимо формальных параметров (локальные, глобальные переменные) понадобятся для реализации алгоритма.
Описать алгоритм словами или в виде блок-схемы.
Описать алгоритм в виде программы-функции на языке MathCAD.
Основы рисунка
Дата добавления: 2015-01-10; просмотров: 1038;
