Использование матриц специального вида для выполнения матричных операций в системе MathCad
Известно, что в результате умножении матрицы на вектор получается вектор. Причем, каждый i–ый элемент этого вектора-результата представляет собой сумму попарных произведений соответствующих элементов i–ой строки матрицы на элементы вектора-сомножителя. Очевидно, если в векторе, на который умножается матрица, все элементы равны нулю, а один элемент равен единице, то результатом такого произведения будет число, соответствующее тому элементу i–ой строки матрицы, где векторным сомножителем будет единица. Такой вывод можно использовать для выделения (формирования) из матрицы нужного столбца.
Пример 9. Даны матрица: А(4x4). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 0–ым столбцом матрицы А, а второй — с 3-им столбцом матрицы А.
Решение.Для получения новых векторов сформируем два вспомогательных вектора: вектор B1 – с единичным значением в строке с номером 0, а второй вектор В4 – с единичным значением в строке с номером 3. Тогда для получения векторов в соответствии с условием задачи достаточно умножить матрицу А справа на векторы В1 и В2, как это показано на рис. 7.12.

| 
|
Рис. 7.12. Выделение векторных значений из заданной матрицы
Аналогичным образом можно получить вектор-строку из матрицы. Для этого достаточно сформировать вспомогательный вектор - строку, у которой все компоненты равны нулю, а одна компонента, номер которой соответствует номеру выделяемой строки из матрицы, равна единице. Если этот вектор умножить слева на матрицу, то в результате будет получена нужная строка.
Пример 10. Дана матрица: А(4x4). Требуется выделить из матрицы первую строку по порядку (с номером 0).
Решение. Сначала требуется подготовить вспомогательный вектор-строку, а потом умножить эту строку слева на матрицу А. Вектор-строку можно получить из предыдущего примера транспонированием вектора-столбца В1.
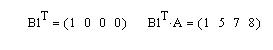
Такой прием можно использовать для перестановки строк и столбцов матрицы, только для этого потребуется уже вспомогательная матрица, состоящая из векторов-столбцов (векторов-строк), место единичных элементы которых соответствуют тому порядку, который нужно иметь в результате преобразования матрицы.
Пример 11. Дана матрица: А(4x4). Требуется переставить в матрице строки с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в строках должно соответствовать нужному порядку для расположения строк в новой матрице. После этого решение можно получить простым перемножением матриц:
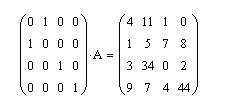
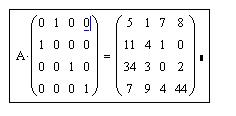
Пример 12. Дана матрица: А(4x4). Требуется переставить в матрице столбцы с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в столбцах соответствуют нужному порядку для выбора их в новую матрицу. После этого решение можно получить простым перемножением матриц:
Рассуждая, таким образом, можно с помощью вспомогательного вектора с единичными компонентами получить вектор, компоненты которого будут равны сумме строк (столбцов) матрицы, а также суммы отдельно выделенного столбика (строчки).
Пример 13. Дана матрица: А(4x4). Требуется найти сумму элементов в столбце с номером 3.
Решение. Для решения задачи требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:
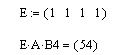
Пример 14. Дана матрица: А(4x4). Требуется получить вектора, элементы которого будут представлять суммы элементов в столбцах матрицы.
Решение. Для решения требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:
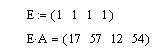
Дата добавления: 2015-01-10; просмотров: 1343;
