Ввод-вывод двухмерного массива
Для поэлементного ввода и вывода матрицы используется двойной цикл for.... Если задать индекс i как параметр внешнего цикла, а индекс j как параметр внутреннего цикла, то ввод-вывод матрицы осуществляется построчно.
Пример 1.Организовать ввод целочисленной матрицы М по строкам.
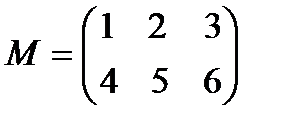
Описание матрицы вместе с текущими индексами имеет вид:
int main()
{
int М[2][3] ;
int i, j;
Ввод в программе реализуется в форме диалога, т.е. сопровождается выводом поясняющего сообщения:
printf("Введите матрицу М\n");
for( i = 0; i<2; i++)
for( j = 0; j< 3; j++)
scanf("%f",&m[i][j]);
Аналогично для ввода матрицы можно использовать функцию cin:
cout<<"Введите матрицу М\n";
for( i = 0; i<2; i++)
for( j = 0; j< 3; j++)
cin>>m[i][j];
На клавиатуре желательно для наглядности восприятия набирать элементы матрицы по строкам, отделяя числа друг от друга одним или несколькими пробелами:
1 2 3 [Enter]
4 5 6 [Enter]
Пример 2.Организовать вывод матрицы М на экран.
Вывод матрицы необходимо реализовать в удобном для чтения виде, т.е. чтобы на одной строке экрана располагалась одна строка матрицы. С этой целью в тело внешнего цикла, помимо внутреннего цикла, включается оператор printf, который переводит курсор к началу следующей строки экрана после вывода текущей строки матрицы.
for ( i = 0; i<2; i++)
{
for ( j = 0; j< 3; j++)
printf("%3d ",m[i][j]);
printf("\n");
}
Вид матрицы на экране будет следующим:
1 2 3
4 5 6
Вывод матрицы можно реализовать и с помощью функции cout:
for ( i = 0; i<2; i++)
{ for ( j = 0; j< 3; j++)
cout<<m[i][j]<<"\t";
cout<<"\n";
}
Прежде чем приступись к разбору задач обработки матриц, следует знать следующее.
Квадратная матрица – это двумерный массив, в котором количество строк равно количеству столбцов. Квадратная матрица имеет главную и побочную диагонали. Главной диагональю матрицы называется диагональ, идущая из левого верхнего угла в правый нижний угол матрицы, например,
для матрица M[3][3]:
| М00 | М01 | М02 |
| М10 | М11 | М12 |
| М20 | М21 | М22 |
элементы М00 М11 М22 – элементы главной диагонали. Обращение к элементу главной диагонали выглядит как М[i][i].
Побочной диагональю матрицы называется диагональ, идущая из левого нижнего угла в правый верхний угол матрицы.
| М00 | М01 | М02 |
| М10 | М11 | М12 |
| М20 | М21 | М22 |
Обращение к элементу побочной диагонали выглядит как М[i][n-1-i], где n- размерность матрицы.
Для любого элемента М[i][j] квадратной матрицы следует заметить следующее: если учесть, что индексы элементов матрицы изменяются от 0 до n-1, то
1) если i==j , элемент расположен на главной диагонали;
2) если i>j, элемент расположен ниже главной диагонали;
3) если i<j, элемент расположен выше главной диагонали;
4) если i>= j. элемент расположен на главной диагонали и ниже;
5) если i<= j, элемент расположен на главной диагонали и выше;
6) если i+j <=n-1 – элемент расположен над побочной диагональю;
7) если i+j>n-1 – элемент расположен под побочной диагональю;
Дата добавления: 2015-02-10; просмотров: 1305;
