Установившиеся ошибки при гармоническом воздействии
Если главная передаточная функция замкнутой системы имеет вид 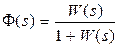 , то при входном сигнале
, то при входном сигнале 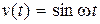 выходной сигнал в установившемся режиме
выходной сигнал в установившемся режиме 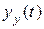 будет определяться выражением
будет определяться выражением
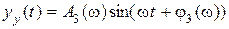 , (6.13)
, (6.13)
где 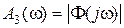 ,
, 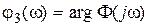 .
.
Аналогично, зная 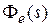 , можно найти закон изменения ошибки в установившемся режиме при гармоническом входном сигнале
, можно найти закон изменения ошибки в установившемся режиме при гармоническом входном сигнале 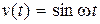 :
:
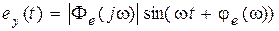 , (6.14)
, (6.14)
где 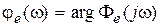 .
.
Выражения (6.13), (6.14) позволяют оценить ошибки воспроизведения гармонического сигнала в установившемся режиме. Из этих выражений следует, что кроме ошибки воспроизведения амплитуды входного гармонического сигнала существуют и постоянные фазовые ошибки, которые определяются видом фазочастотных характеристик замкнутой системы. Обычно при анализе точности систем управления их не рассматривают, ограничиваясь лишь анализом ошибок воспроизведения амплитуды.
Из (6.13), (6.14) можно получить ошибки воспроизведения амплитуды гармонического сигнала на заданной частоте, равные
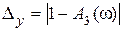 , (6.15)
, (6.15)
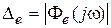 , (6.16)
, (6.16)
первая из которых характеризует разность между максимальными значениями амплитуды входного и выходного сигналов, а вторая – максимальную величину ошибки 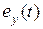 . Очевидно, всегда
. Очевидно, всегда 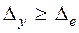 . Так как
. Так как 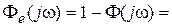
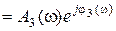 то
то 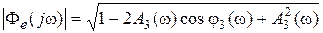 . Если
. Если 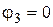 , то
, то  . Таким образом, при малых фазовых сдвигах на заданной частоте
. Таким образом, при малых фазовых сдвигах на заданной частоте 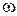 оценки (6.15) и (6.16) будут близки между собой. Это обычно выполняется в диапазоне низких частот.
оценки (6.15) и (6.16) будут близки между собой. Это обычно выполняется в диапазоне низких частот.
На рис. 6.2 представлен типичный вид АЧХ замкнутой системы 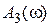 для случая астатической системы, при этом
для случая астатической системы, при этом 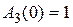 . В случае статической системы
. В случае статической системы 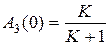 . На рисунке заштрихованная область соответствует величинам ошибок
. На рисунке заштрихованная область соответствует величинам ошибок 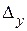 .
.
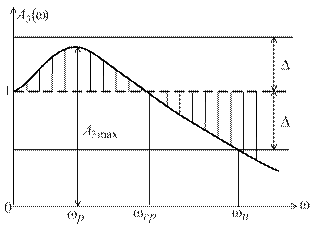
Рис. 6.2
Под полосой пропускания системы понимают диапазон частот 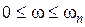 , при котором ошибка
, при котором ошибка 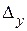 будет меньше некоторой заданной
будет меньше некоторой заданной 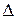 , т.е.
, т.е. 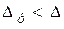 . Иногда полосу пропускания определяют как диапазон частот
. Иногда полосу пропускания определяют как диапазон частот 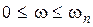 , при котором выполняется условие
, при котором выполняется условие 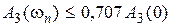 .
.
Полоса пропускания является важной характеристикой системы. С одной стороны, чем шире полоса пропускания, тем с меньшими ошибками система воспроизводит управляющие сигналы. Однако, с другой стороны, увеличение  приводит к тому, что система становится чувствительной к влиянию высокочастотных помех.
приводит к тому, что система становится чувствительной к влиянию высокочастотных помех.
Из выражения (6.16) можно получить приближенные оценки величины ошибки 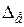 . Так как
. Так как 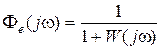 , то для статической системы
, то для статической системы 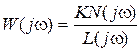 и при достаточно низких частотах можно полагать
и при достаточно низких частотах можно полагать 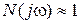 ,
, 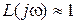 ,
, 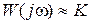 , откуда имеем
, откуда имеем
 . (6.17)
. (6.17)
Для астатической системы 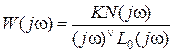 и при низких частотах
и при низких частотах 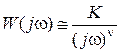 , откуда получим
, откуда получим
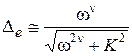 . (6.18)
. (6.18)
Если выполняется условие 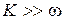 , то формула (6.18) принимает вид
, то формула (6.18) принимает вид
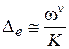 . (6. 19)
. (6. 19)
Из (6.17)–(6.19) видно, что ошибка системы обратно пропорциональна коэффициенту усиления разомкнутой системы.
Итак, для повышения точности САУ следует увеличивать коэффициент усиления разомкнутой системы либо увеличивать порядок астатизма. Однако это будет приводить в общем случае к ухудшению устойчивости. Таким образом, требования к точности системы и ее устойчивости являются противоречивыми.
Пример 6.3. Пусть передаточная функция разомкнутой системы имеет вид 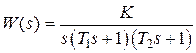 при
при 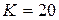 ,
, 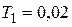 с,
с, 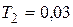 с,
с, 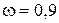 с-1.
с-1.
Передаточная функция системы по ошибке 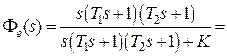
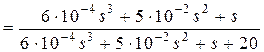 . Находим величину
. Находим величину 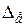 (6.16):
(6.16): 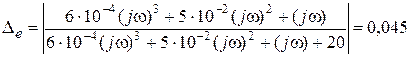 с-1. Если воспользоваться приближенной формулой (6.19), то
с-1. Если воспользоваться приближенной формулой (6.19), то 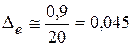 с-1, т.e. с точностью до третьего знака оба результата совпадают.
с-1, т.e. с точностью до третьего знака оба результата совпадают.
7. ОЦЕНКИ КАЧЕСТВА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Численные величины, характеризующие работу системы автоматического управления, носят название показателей качества, которые условно можно разделить на три группы: характеризующие а) устойчивость системы, б) точность системы и в) качество переходных процессов. Обеспечение устойчивости является необходимым условием функционирования любой системы управления и гарантирует затухание свободной или переходной составляющей процесса. К этой первой группе показателей относятся запасы устойчивости по амплитуде 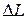 и фазе
и фазе 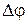 .
.
После затухания свободной составляющей через достаточно большой промежуток времени в системе протекает установившийся процесс, который обуславливает точность системы. Показателями качества в данном случае выступают величины ошибок в установившемся режиме, которые рассмотрены в разд. 6 (вторая группа).
Наконец, к третьей группе относятся показатели качества переходного процесса, которые характеризуют вид процесса для достаточно малых моментов времени после его начала. Среди таких показателей – время регулирования 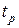 , перерегулирование
, перерегулирование 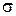 и ряд других, приведенных в подразд. 4.1.
и ряд других, приведенных в подразд. 4.1.
Показатели качества могут быть вычислены двумя способами. Первый –непосредственно по виду переходного процесса. В этом случае их называют прямыми оценками качества. Второй способ – это использование косвенных оценок показателей качества без построения кривой переходного процесса.
В данном разделе рассмотрим наиболее распространенные косвенные методы оценки показателей качества переходного процесса.
Дата добавления: 2015-02-07; просмотров: 2213;
