Понятие устойчивости линейных систем

Общие определения устойчивости процессов, справедливые как для линейных, так и для нелинейных систем, будут даны во второй части конспекта лекций. Здесь отметим, что свойство устойчивости или неустойчивости заданного процесса, протекающего в системе, рассматривается по отношению к другим процессам той же системы, отличающимся от заданного за счет изменений начальных условий. величинами, отклоняющими процесс от заданного, являются возмущения начальных условий.

Для случая линейной системы динамические процессы в ней описываются линейным дифференциальным уравнением:

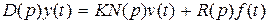, (5.1)

общее решение которого определяется выражением (4.3): .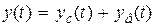

Изменение начальных условий влияет только на поведение свободной составляющей и не влияет на 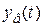, откуда следует, что устойчивость будет определяться поведением свободной составляющей. Если 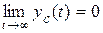, тo процессы в линейной системе будем называть асимптотичeски устойчивыми, при 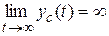– нeустойчивыми, и если при любом 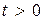свободная составляющая ограничена, то процессы будут просто устойчивы. Если одно из указанных свойств присуще какому-либо процессу, то для линейной системы оно будет справедливо для всех процессов. Поэтому принято говорить об асимптотической устойчивости, неустойчивости или просто устойчивости линейной системы. В последнем случае еще говорят, что линейная система находится на границе устойчивости или является нeйтpальной.

Структура свободной составляющей имеет вид (4.4) или (4.5).

Из (4.4), (4.5) следует, что поведение свободной составляющей во времени не зависит от величин 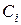и соответственно от начальных условий, а полностью определяется видом корней .

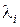В комплексной плоскости корней корни интерпретируются как соответствующие точки. Если корень 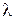лежит слева от мнимой оси, т. е. 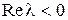, будем называть его лeвым коpнeм, если 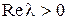– пpавым.

Пусть 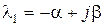, 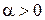– левый корень, тогда составляющая 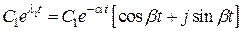в (4.4) при 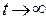будет затухать и стремиться
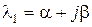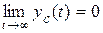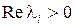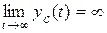к 0, а в случае правого корня – наоборот возрастать до бесконечности. Таким образом, при различных корнях характеристического уравнения, если все корни левые, , что соответствует факту асимптотической устойчивости системы. Если хотя бы один корень правый ( ), то и система будет неустойчива. Если для всех различных корней справедливо соотношение 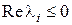, то в свободной составляющей появятся слагаемые, которые будут либо постоянными (нулевой корень), либо будут изменяться по гармоническому закону (чисто мнимые корни), и составляющая 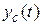будет ограничена, что соответствует нейтральной системе.

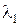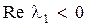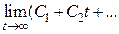
В случае кратного корня , если , , 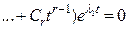так как при любом 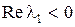функция 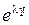затухает быстрее, чем возрастает функция в скобках. Если же 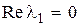, то это утверждение не правомерно.

Таким образом, необходимым и достаточным условием асимптотической устойчивости линейной системы, описываемой уравнением (5.1), является выполнение соотношения 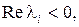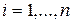. Система будет просто устойчива, если 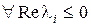и среди корней, лежащих на мнимой оси, нет кратных. Система будет неустойчива, если имеется хотя бы один корень, для которого 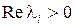, или хотя бы один кратный корень, лежащий на мнимой оси.

Суждение об устойчивости можно сделать, найдя корни характеристического уравнения замкнутой системы

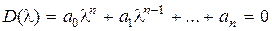. (5.2)

Эту задачу можно упростить, так как фактически нам достаточно знать лишь расположение корней в плоскости корней относительно мнимой оси, которую называют границей устойчивости. Выделяют три типа границы устойчивости: aпepиодичeского типа, которая характеризуется нулевым корнем характеристического уравнения, колeбательного типа, что соответствует наличию пары чисто мнимых корней, и границу, соответствующую бесконечно удаленному корню ( 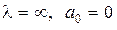(5.2)). Если все корни уравнения (5.2) лежат слева от мнимой оси, т.е.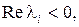 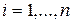, то характеристический полином 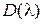будем называть полиномом Гуpвица, или гуpвицeвым полиномом.

Определение расположения корней уравнения (5.2) относительно мнимой оси без их непосредственного вычисления производят на основе критериев устойчивости, которые делятся на две группы: алгебраические и частотные.