Краткая теория. В 1879 г. американский физик Эдвин Герберт Холл (E.H
В 1879 г. американский физик Эдвин Герберт Холл (E.H. Hall, 1855–1938) обнаружил, что при помещении тонкой пластины с током I в магнитное поле, перпендикулярное плоскости пластины, в ней возникает поперечная разность потенциалов, которую назвали напряжением Холла. Проведённые измерения показали, что холловское напряжение U прямо пропорционально индукции В магнитного поля и силе тока I, и обратно пропорционально толщине d пластины:
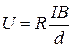 , ,
| (8.2) |
где R – коэффициент пропорциональности (коэффициент Холла), его знак и величина зависят от заряда носителей тока и их концентрации.
Рассмотрим элементарную теорию эффекта Холла. Пусть носителями тока являются электроны (например, в металлах и в полупроводниках n-типа). При протекании в образце тока плотностью j электроны имеют скорость направленного движения u (скорость дрейфа), направленную против направления тока (рис. 8.1). Если проводник с током помещён в магнитное поле, то на электроны действует сила Лоренца:
FЛ = 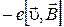 , ,
| (8.2) |
направленная перпендикулярно их скорости (см. рис. 8.1). Электроны будут отклоняться к одной из граней, оставляя на противоположной стороне пластины не скомпенсированный положительный заряд.
В результате вдоль оси Y появится поперечное электрическое поле, действующее на электрон с силой
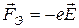 , ,
| (8.3) |
 которая направлена противоположно силе Лоренца. Накопление зарядов будет продолжаться до тех пор, пока возникшее электрическое поле не скомпенсирует отклоняющее действие магнитного поля. При равенстве модулей сил
которая направлена противоположно силе Лоренца. Накопление зарядов будет продолжаться до тех пор, пока возникшее электрическое поле не скомпенсирует отклоняющее действие магнитного поля. При равенстве модулей сил
| eE = euB | (8.4) |
установится стационарное состояние, то есть постоянное поперечное электрическое поле Холла, напряжённость которого
| E = uB, | (8.5) |
если магнитное поле перпендикулярно скорости дрейфа электронов.
Полагая поперечное электрическое поле однородным, найдём разность потенциалов между противоположными гранями пластины (напряжение Холла)
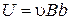 , ,
| (8.6) |
где b – ширина пластины, илиразмер образца вдоль направления поля Холла.
Скорость u электронов можно выразить через силу тока:
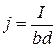 ; j = enu; Þ ; j = enu; Þ 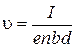 , ,
| (8.7) |
где n – концентрация носителей тока в пластине.
Подставив скорость (8.7) в равенство (8.6), получим напряжение Холла
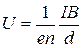 . .
| (8.8) |
Сравнивая выражения (8.1) и (8.8), получаем коэффициент Холла
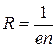 . .
| (8.9) |
Из этой формулы следует, что знак коэффициента Холла определяется знаком заряда носителей тока. Для металлов и полупроводников n-типа R < 0, а для полупроводников с дырочной проводимостью (р-типа) R > 0.
Дата добавления: 2015-02-07; просмотров: 1035;
