Определение эффективного числа приёмников при трёхфазных нагрузках
Полным выражением для определения эффективного числа приёмников является 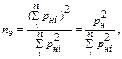 , которое даёт точное значение
, которое даёт точное значение 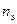 , где в числителе квадрат групповой мощности, а в знаменателе – сумма квадратов номинальных активных мощностей отдельных приёмников группы.
, где в числителе квадрат групповой мощности, а в знаменателе – сумма квадратов номинальных активных мощностей отдельных приёмников группы.
Так же существуют способы упрощенного вычисления 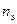 .
.
1. При числе фактических приёмников в группе 4 и более допускается эффективное число приёмников 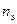 считать равным фактическому
считать равным фактическому  при величине отношения
при величине отношения 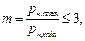 где в числителе и знаменателе активные мощности наибольшего и наименьшего приёмников в группе.
где в числителе и знаменателе активные мощности наибольшего и наименьшего приёмников в группе.
По данному способу, при определении 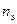 , могут быть исключены те наименьшие приёмники группы, суммарная номинальная мощность которых не превышает 5 % суммарной мощности всей группы (при этом число исключённых приёмников не учитывается также и в величине
, могут быть исключены те наименьшие приёмники группы, суммарная номинальная мощность которых не превышает 5 % суммарной мощности всей группы (при этом число исключённых приёмников не учитывается также и в величине  ).
).
2. При 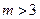 и
и 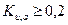 эффективное число приёмников может быть определено по формуле
эффективное число приёмников может быть определено по формуле 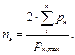 Если определение
Если определение 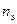 по данному методу оказывается большим, чем фактическое, то следует принимать
по данному методу оказывается большим, чем фактическое, то следует принимать 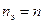 .
.
3. При невозможности использования способов приведённых в пунктах 1 и 2, определение 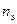 можно выполнить с помощью кривых, построенных по формуле
можно выполнить с помощью кривых, построенных по формуле 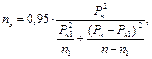
или в относительных единицах 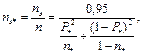 где
где 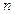 - фактическое число приёмников в рассматриваемой группе;
- фактическое число приёмников в рассматриваемой группе; 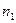 - число наибольших приёмников в группе, мощность каждого из которых не менее половины мощности наибольшего приёмника;
- число наибольших приёмников в группе, мощность каждого из которых не менее половины мощности наибольшего приёмника; 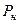 - суммарная номинальная мощность приёмников всей группы;
- суммарная номинальная мощность приёмников всей группы; 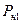 - суммарная номинальная мощность
- суммарная номинальная мощность 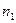 приёмников группы;
приёмников группы; 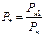 .
.
Порядок определения 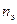 следующий:
следующий:
· Выбирается наибольший по номинальной мощности приёмник рассматриваемой группы.
· Выбираются наиболее крупные приёмники, номинальная мощность которых равна или больше половины мощности наибольшего приёмника группы.
· Определяют число 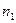 и суммарную номинальную мощность
и суммарную номинальную мощность 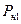 наибольших приёмников группы.
наибольших приёмников группы.
· Определяют число 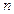 и суммарную номинальную мощность
и суммарную номинальную мощность 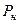 всех приёмников группы.
всех приёмников группы.
· Находят значения 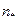 и
и 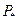 .
.
· По кривым, построенным на основании выражений (3.78) и (3.79), по найденным значениям 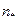 и
и 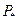 определяется величина
определяется величина 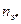 , а затем из выражения
, а затем из выражения 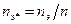 находится
находится 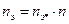 .
.
Дата добавления: 2015-02-05; просмотров: 1170;
