Разновидности компьютерной графики

В рассмотренных выше транспортных задачах передача мощностей осуществлялась непосредственно от источников к потребителям. Это транспортные задачи в так называемой классической постановке.

В реальных схемах электрических сетей часто оказывается целесообразной передача мощности через промежуточные (транзитные) узлы. Такими транзитными узлами могут быть как узлы источников питания, так и узлы потребителей. На рис. 3.6 в качестве примера приведены простейшие схемы электрических сетей, поясняющие понятие "транзит мощности".

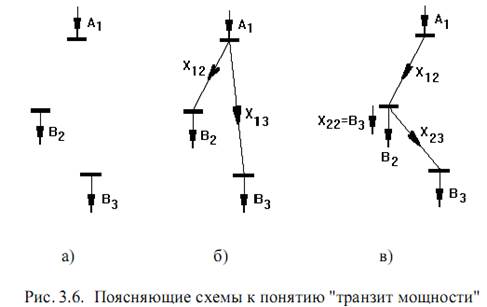
На рис.3.6,а показано взаимное расположение узлов источника А₁ и потребителей В₂ и В₃. При классической постановке транспортной задачи оптимальная схема электрической сети будет иметь вид, показанный на рис. 3.6,б. Очень возможно, что эта схема будет дороже, чем схема, приведенная на рис. 3.6,в, в которой мощность к потребителю B₃ передается через промежуточный (транзитный) узел потребителя В₂. Величина транзитной мощности, передаваемой через узел В₂, равна мощности потребителя В₃, т.е. x₂₂=В₃.

Транзитная мощность обозначена переменной с двумя одинаковыми индексами, соответствующими номеру узла, через который она протекает. Можно показать, что транзитным узлом может быть и узел источника питания.

Таким образом, транспортная задача с транзитом мощности является более общей задачей и имеет более широкие возможности по оптимизации схемы электрической сети, чем транспортная задача в классической постановке.

При решении транспортных задач с транзитом мощности с количеством источников п и количеством потребителей т всем узлам схемы присваивается единая нумерация 1,2,... (n+m).

Целевая функция представляет собой сумму произведений удельных стоимостей на величины передаваемых мощностей от узла i к узлу j

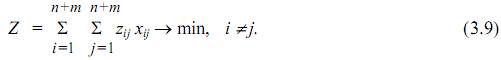
Стоимость передачи мощности между узлами i и j не зависит от направления этой мощности, поэтому в рассматриваемой задаче принимается z_ij=z_ji.

Для оценки удельных затрат z_ii на передачу через i-й узел транзитной мощности х_ii обратимся к рис. 3.6, в. Затраты на электрическую сеть, показанную на этом рисунке, составляют Z= z₁₂x₁₂+z₂₃x₂₃. Транзитная мощность х₂₂ и удельные затраты z₂₂ на ее передачу через узел 2 не входят в выражение целевой функции Z. Следовательно, удельные затраты на передачу транзитной мощности через любой i-й узел z_ii=0.

Как и в классической транспортной задаче, ограничениями в транспортной задаче с транзитом будут балансы мощности во всех узлах. В частности, для узла В₂ схемы рис. 3.6, в баланс мощности запишется в виде х₁₂ = В₂ + х₂₂ или x₁₂-x₂₂=B₂.

В общем случае для любого j-го потребителя сумма мощностей, притекающих от всех других узлов, за вычетом транзитной мощности х_jj равна мощности этого потребителя.

Аналогично можно записать уравнение баланса мощности для любого i-го источника. Сумма мощностей, оттекающих от i-го источника ко всем другим узлам, за вычетом транзитной мощности х_ii равна мощности этого источника.

Из двух последних выражений видно, что транзитная мощность входит в математическую модель транспортной задачи со знаком минус.

Для решения транспортной задачи с транзитом мощности составляется транспортная матрица. Алгоритм решения транспортной задачи с транзитом мощности практически не отличается от алгоритма решения классической транспортной задачи. Отметим отличительные особенности транспортной задачи с транзитом мощности, часть из которых уже упоминалась выше:

1. Всем п узлам источников и т узлам потребителей присваивается сквозная нумерация 1, 2,... (п+т).

2. Считается, что через любой i-й узел может передаваться
транзитная (промежуточная) мощность x_ii.

3. Удельные стоимости передачи транзитной мощности z_ii=0.

4. Транспортная матрица является квадратной и имеет
размерность (п+т)(п+т).

5. Транзитные переменные х_ii входят в решение задачи (в транспортную матрицу) со знаком минус.

6. Вне зависимости от значения все транзитные переменные считаются базисными.

Пример 6. В проектируемой системе электроснабжения имеется 2 узла источников питания и 2 узла потребителей. Мощности источников составляют А₁=100 и А₂=50, а мощности потребителей В₃=90 и В₄=60 е.м. Удельные затраты на передачу мощностей по линиям между узлами составляют z₁₂=10, z₁₃=5, z₁₄=2, z₂₃=4, z₂₄=3 и z₃₄=2 у.е./е.м.

Требуется найти оптимальную схему электрической сети.

Решение. В соответствии с условиями задачи принята следующая сквозная нумерация узлов А₁, А₂, B₃ и В₄. Составим транспортную матрицу. Эта матрица будет квадратной размерностью 4x4 (табл. 3.10).

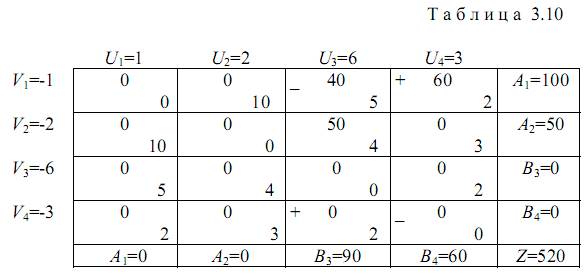
Справа от матрицы, где помещены мощности источников питания, указаны нулевые мощности узлов 3 и 4 (B₃=0, B₄=0), поскольку эти узлы не являются источниками. Снизу под матрицей, где помещены мощности потребителей, указаны нулевые мощности узлов 1 и 2 (A₁=0, А₂=0), поскольку эти узлы не являются потребителями.

Исходное допустимое решение найдено методом наименьшей удельной стоимости. В полученном допустимом решении

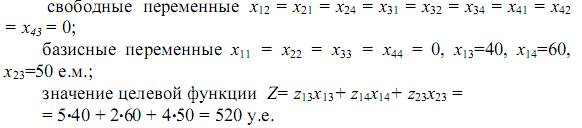
Присвоим каждой строке потенциал V_i а каждому столбцу -потенциал U_j. В соответствии с методом потенциалов для всех базисных переменных сумма потенциалов равна удельной стоимости

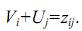
Зададимся произвольно значением одного из потенциалов (U₁=1). Вычисленные значения остальных потенциалов показаны в табл. 3.10. Поскольку для базисных транзитных переменных удельные стоимости z_ii = 0, потенциалы с одинаковыми индексами равны по величине и противоположны по знаку V_i= -U_i.

Полученному исходному допустимому решению отвечает схема электрической сети, приведенная на рис. 3.7,а. Попробуем улучшить полученное решение.

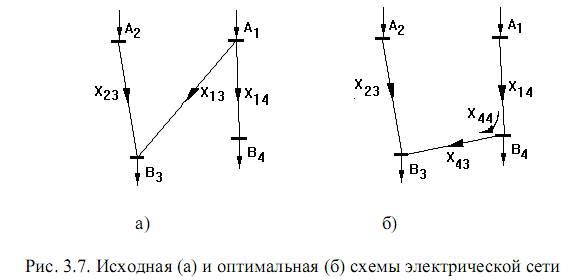
Для всех свободных переменных проверим соотношение суммы потенциалов с удельной стоимостью. Для свободной переменной х₃₄

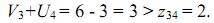
Следовательно, свободную переменную х₃₄ следует перевести в базис. Для этой переменной строим цикл (табл. 3.10). Начальная вершина цикла лежит в клетке свободной переменной х₃₄. Остальные вершины цикла лежат в клетках, соответствующих базисным переменным x₁₃, x₁₄ и х₄₄. Начальной вершине присваиваем знак "+", далее знаки вершин цикла чередуются.

При увеличении свободной переменной х₄₃ базисная переменная x₁₄ будет увеличиваться, а базисные переменные x₁₃ и х₄₄ будут уменьшаться. Поскольку транзитная базисная переменная х₄₄ входит в решение задачи со знаком "минус", ее изменение в отрицательную сторону не ограничено. Уменьшение базисной переменной x₁₃=40 ограничено нулевым значением. Поэтому значения всех переменных в вершинах цикла следует изменить на 40 е.м.

В новом допустимом решении (табл. 3.11)

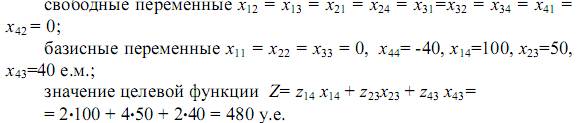
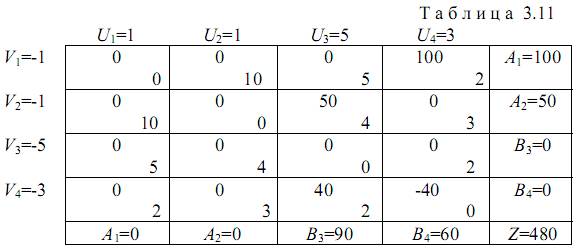
В этом решении для всех свободных переменных выполняется условие (3.8). Следовательно, перевод любой свободной переменной в базис не улучшит решения. Полученное решение является оптимальным. Оптимальная схема электрической сети показана на рис. 3.7, б.

Разновидности компьютерной графики

Распространение компьютерной графики началось с полиграфии. Но вскоре она вы­рвалась из тесных помещений типографий на простор широкого применения. Огромную популярность завоевали компьютерные игры, научная графика и фильмы. Сейчас без развитой и изо­щренной графики не обходится ни один фантастический фильм, ни одна компьютер­ная игрушка. Создаются изображения настолько реальные, что трудно поверить в то, что все это создано на компьютере. Мощнейшие машины и талантливейшие команды математиков, программистов и дизайнеров работают над этим. Ни один приличный доклад в сфере бизнеса не обходится сейчас без компьютерной презентации.

Из простого перечисления областей применения видно, что понятие компьютер­ной графики довольно обширно — от алгоритмов, рисующих на экране причудли­вые узоры, до мощных пакетов ЗD-графики и программ, имитирующих классиче­ские инструменты художника. Иными словами, компьютерная графика не являет­ся простым рисованием при помощи компьютера, а представляет собой довольно сложный комплекс, который находит применение во многих областях человеческой деятельности:

· двухмерная графика;

· полиграфия;

· web-дизайн;

· мультимедиа;

· ЗD-графика и компьютерная анимация;

· видеомонтаж;

· САПР и деловая графика;

· геоинформационные системы.

Сферы применения компьютерной графики чрезвычайно разнообразны. Каждый ее раздел имеет свои отличительные особенности и тонкости «технологи­ческого производства». Для каждого из них создано свое программное обеспече­ние, включающее разнообразные специальные программы (графические редакто­ры). Вне зависимости от области использования каждый графический редактор, как правило, должен иметь:

● инструменты рисования на компьютер;

● библиотеку готовых изображений;

● набор шрифтов;

● набор спецэффектов;

● а также быть совместимым с другими графическими программами.

Остановимся на некоторых характерных чертах, присущих отдельным областям компьютерной графики, попутно затрагивая используемые в них программные средства.