Деформации. Гипотеза плоских сечений

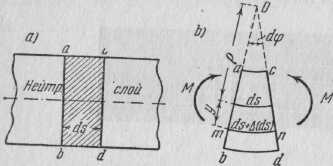
Характер деформации при чистом изгибе легко выяснить при помощи опыта с резиновой моделью бруса прямоугольного сечения с нанесенной на боковых гранях сеткой квадратиков (рис. 3.1, а). При изгибе такого бруса двумя парами, приложенными по концам, можно видеть удлинение горизонтальных граней квадратиков у выпуклой стороны бруса и укорочение граней у вогнутой стороны* сопровождаемые искривлением этих граней (рис. 3.1b). Значит опыт с очевидностью показывает, что продольные волокна изогнутого бруса удлиняются у выпуклой его стороны и укорачиваются у вогнутой.

Так как переход от удлинения к укорочению происходит непрерывно, то внутри бруса существует слой волокон, которые искривляются, но не меняют своей длины. Такой слой называется нейтральным слоем, а его след на плоскости сечения — нейтральной линией илинейтральной осью.

На модели видно, что поперечные линии сетки наклоняются друг к другу, оставаясь прямыми и нормальными

Рис. 3.1.

к искривленным продольным линиям. При этом углы деформированных квадратиков остаются прямыми, что указывает на отсутствие деформаций сдвига, состоящих именно в изменении углов прямоугольных элементов. Если же не наблюдается деформаций сдвига, то не должно быть и связанных с ними касательных напряжений. Таким образом, опыт подтверждает сделанное выше заключение об отсутствии касательных напряжений при чистом изгибе. Искривление сетки квадратиков на обеих боковых поверхностях бруса в силу симметрии сечения будет совершенно одинаковым.

Естественно предположить, что картина распределения деформаций, наблюдаемая на поверхности бруса, имеет место и внутри него. Иначе говоря, во всех плоскостях, параллельных боковым, закон постепенного перехода от удлинения к укорочению волокон одинаков. В таком случае нейтральный слой волоконпредставляет собой до изгиба плоскость и после изгиба цилиндрическую поверхность. В силу симметрии сечения относительно плоскости действия внешних сил изгиб происходит в той же плоскости, т. е. прямая и изогнутая оси бруса лежат в одной плоскости ху (рис, 3.1). При этомнейтральная ось

есть прямая, перпендикулярная к оси симметрии у. Поперечные сечения бруса взаимно наклоняются, вращаясь вокруг своих нейтральных осей.

Вывод: сечения, плоские и нормальные к оса бруса до изгиба, остаются и после изгиба плоскими и нормальными к изогнутой оси бруса. Положение это, подтвержденное многочисленными опытами, принимается в сопротивлении материалов в качестве рабочей гипотезы и носит название «гипотезы плоских сечений» или «гипотезы Бернулли» по имени ученого Я. Бернулли, впервые ее высказавшего в 1705 г.

Пользуясь этой гипотезой, установим закон изменения удлинений волокон по высоте бруса. Двумя весьма близкими по перечными сечениями а — bнс—d выделим элемент бруса длиной ds

(рис. 2 а). После изгиба сечения образуют элементарный угол 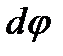и все волокна искривятся, имея в точке О общий центр кривизны. Волокна нейтрального слоя сохранят при этом прежнюю длину ds, при положительном изгибающем моменте выпуклость будет обращена вниз (рис. 160, б). Положительная ось у направлена вверх и начало координат

Рис 2. помещено в произвольной ее точке. Координатную ось z совместим с нейтральной осью сечения. Тогда расстояние какого-либо волокна тп (рис. 2, б) до нейтрального слоя будет равно величине координаты у соответствующей точки т сечения.

Обозначим радиус кривизны нейтрального волокна через р. Тогда волокно тп будет иметь радиус кривизны 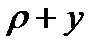и длину .

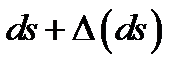Абсолютное удлинение волокна тп : .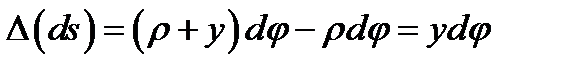

Относительное удлинение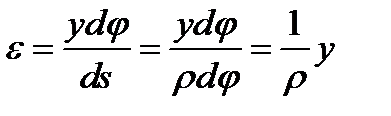

Здесь 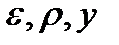имеют абсолютные значения величин . Кривизну 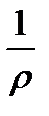принято считать положительной, если центр кривизны обращен в положительную сторону оси у, и отрицательной в обратном случае. В нашем случае 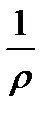> 0 и у < 0, поэтому правая часть предыдущего равенства отрицательна, в то время как удлинение волокна тп, расположенного с выпуклой стороны, положительно. Чтобы привести в соответствие знаки обеих частей, равенство следует записать так:

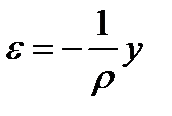(3.5)

Таким образом, удлинения волокон пропорциональны их расстояниям до нейтрального слоя.

Простое растяжение и сжатие сопровождается поперечной деформацией сечения, определяемой коэффициентом Пуассона, причем отдельные волокна изменяют свою длину, не оказывая давления друг на друга. Опыт показывает, что при изгибе также происходит изменение формы поперечного сечения: оно сужается у выпуклой стороны бруса и расширяется у вогнутой стороны, принимая вид, показанный (для случая прямоугольного сечения) на рис. 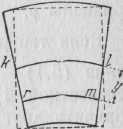161 сплошными линиями. Боковые стороны сечения взаимно наклоняются, вращаясь около точек k и l. Поперечные волокна изменяют длину и искривляются выпуклостью в сторону, обратную выпуклости продольных волокон. Нейтральная линия kl искривляется без изменения длины. Если допустить, что при чистом изгибе имеют место простое растяжение и сжатие продольных волокон бруса,

Рис. 3 т. е. что волокна не нажимают друг на друга, то относительные удлинения поперечного и продольного волокон, равноотстоящих от нейтрального слоя, должны находиться в отношении, равном коэффициенту Пуассона:

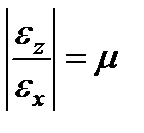
где e_z — поперечная относительная деформация.

Определение обоих удлинени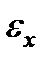й и 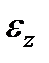опытным путем подтверждает сделанное допущение. Значения 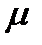, полученные из опытов на изгиб и на простое растяжение, оказываются весьма близкими.

Дата добавления: 2015-01-26; просмотров: 2889;