Распределение нагрузки между телами качения

Если рассматривать распределение нагрузки R, действующей на радиальный шарикоподшипник, то окажется, что эта нагрузка распределяется между телами качения неравномерно. Нагруженная зона составляет не более 180º.

Для упрощения предположим, что тела качения занимают симметричное положение относительно нагрузки, тогда

R = P₀ + 2P₁Cosγ + 2P­₂Cos2γ,

где γ , 2γ, …nγ – углы между направлением силы R и радиальной плоскостью соответствующего шарика.

Осевая сила при точном изготовлении и отсутствии взаимного перекоса колец распределяется между телами качения практически равномерно.

В шарикоподшипниках начальный контакт между шариком и кольцами происходит в точке. После приложения нагрузки зона контакта принимает эллиптическую форму. При этом необходимо, чтобы контактное напряжение в центре этой площадки не превышало допустимого значения (σ_{H max} ≤ [σ]_H), [σ]_H = 5000 МПа.

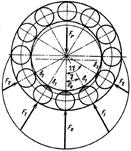
Рис. 21.3. Распределение нагрузки между телами качения

Потери на трение складываются из следующих составляющих:

а) трение между телами качения и кольцами. Этот вид трения состоит из трения качения и дополнительного трения скольжения. Качение в наиболее чистом виде характерно для цилиндрических роликоподшипников. В этом случае все точки линии контакта по длине ролика имеют одинаковую окружную скорость. В шарикоподшипниках и сферических роликоподшипниках контактов в поперечном сечении происходит по дуге. Окружные скорости точек линии контакта различны, что приводит к проскальзыванию и потерям на трение скольжения.

б) трение скольжения тел качения (роликов) в конических роликоподшипниках. В этом случае трение скольжения имеет место между торцевой поверхностью ролика и буртом внутреннего кольца.

в) трение, связанное с погрешностями формы тел качения и колец, переносом роликов и т.д.

г) трение тел качения о сепаратор и сепаратора о кольца

д) сопротивление масла

е) трение в уплотнениях (встроенные уплотнения).

При малых нагрузках основное значение имеют сопротивления, связанные со смазкой и трением в сепараторе, а при более высоких – трение на площадке контакта между телами качения и кольцами.

Момент трения в подшипниках обычно представляется простейшими зависимостями.

M = 0,5·f_R·R·d или M = 0,5·f_A·A·d,

где R и A – радиальная и осевая нагрузки;

f_R и f_A – приведенные коэффициенты трения;

d – диаметр вала.

Более точно момент трения в подшипнике определяется по формуле:

M = 0,5(T + f₀R)d,

где T = cd – сила сопротивления, не зависящая от нагрузки.

Значения коэффициентов f_R , f_A, f₀, и с при окружных скоростях на шейке вала до 10 м/с и умеренной смазке находят из таблицы.