Т е о р и я м е т о д а

Колебания – движения или процессы, характеризующиеся определенной повторяемостью во времени.

Колебания, происходящие за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему, называются свободными или собственными.

Колебания считаются периодическими, если система приходит в положение равновесия через равные промежутки времени. Простейшими периодическими колебаниями являются гармонические, в которых смещение тела или системы от положения равновесия совершается по закону синуса или косинуса.

Груз массой m, подвешенный на упругой пружине и совершающий гармонические колебания под действием упругой силы F_упр = -kx представляет собой пружинный маятник.

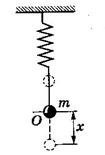
При рассмотрении колебаний пружинного маятника необходимо: пренебречь сопротивлением среды; учесть, что на маятник, находящийся в положении равновесия, действуют две силы: сила тяжести и сила упругости пружины, равные друг другу, но направленные противоположно; при перемещениях маятника вниз от положения равновесия возникает дополнительная сила упругости, направленная к положению равновесия

То же самое будет при отклонении маятника вверх, но природа силы будет иная. Это– равнодействующая силы тяжести и (не полностью компенсирующей ее) силы упругости пружины. По величине эта равнодействующая пропорциональна величине смещения x от положения равновесия маятника. Таким образом, возвращающая сила, действующая на отклоненный маятник - это сила квазиупругая, равная по закону Гука

F_упр = - kx, (1)

где k – коэффициент упругости или жесткость пружины.

Тогда по II закону Ньютона - kx = m 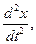(2)

где m – масса маятника, a = 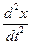- ускорение, равное второй производной смещения по времени.

Преобразовав это уравнение к виду 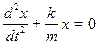(3)

и представив 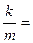w₀² , получим динамическое уравнение свободных незатухающих гармонических колебаний 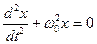(4)

Решением этого дифференциального уравнения является функция

х = А sin (w₀t+j₀) или х = А сos (w₀t + j₀) (5)

Формула (5) выражает смещение х пружинного маятника в любой момент времени t и является кинематическим уравнением гармонического колебания в общем виде.

А – амплитуда -. максимальное отклонение от положения равновесия

(w₀t + j₀) – фаза - величина, определяющая положение колеблющейся системы в любой момент времени t

j₀ – начальная фаза колебания, определяющая положение системы в начальный момент времени t = 0

w₀ – круговая (циклическая) частота - количество полных колебаний за 2p секунды

Время одного полного колебания - период Т

Число полных колебаний, совершаемых в единицу времени – частота колебания ν. Они связаны Т = 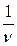w₀ = 2p n

Учитывая, что w₀² = 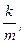получим период колебаний пружинного маятника Т = 2p 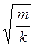(6)

Выясним физический смысл коэффициента упругости k:

k = - 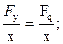(7)

где F_q - внешняя деформирующая сила, в соответствии с III- законом Ньютона F_q = -F_упр. Следовательно, коэффициент упругости k численно равен внешней силе, вызывающей деформацию пружины, равную единице длины.

Свободные колебания, амплитуда которых из–за потерь энергии реальной колебательной системой с течением времени уменьшается, называются затухающими. Такие колебания совершаются при одновременном действии силы упругости F_упр= - kх и силы сопротивления F_с = - r× u

где r – коэффициент сопротивления среды, u - скорость колеблющейся системы. Динамическое дифференциальное уравнение затухающих колебаний 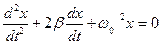(8)

решением которого является кинематическое уравнение:

х = А₀е ^-bt × sin(wt+j₀) (9)

А₀ – начальная амплитуда при t = 0

е - основание натурального логарифма

b = 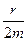- коэффициент затухания j₀ – начальная фаза

w - циклическая частота свободных затухающих колебаний.

Величины циклических частот затухающих и незатухающих колебаний связаны соотношением w² = w²₀ - b². Амплитуда при затухающих свободных колебаниях уменьшается с течением времени по экспоненциальному закону:

А_t = A₀e ^-bt (10)

Скорость затухания колебательного движения характеризуется декрементом затухания, который равен отношению двух последующих амплитуд, разделенных интервалом времени, равным одному периоду колебания (рис. 2)

d = 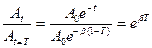(11)

Натуральный логарифм этого отношения называется логарифмическим декрементом затухания:

l = ln 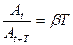(12)

Определив опытным путем период затухающих колебаний можно вычислить коэффициент затухания b и логарифмический декремент затухания l.

Для этого измеряют две амплитуды, отстающие во времени на n периодов, т.е. t = nT.

Равенство отношений 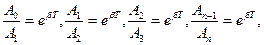позволяет записать 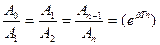(13)

следовательно ln 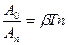(14)

Отсюда коэффициент затухания b = 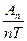(15)