Краткие теоретические сведения. Дискретной называется переменная, содержащая несколько значений, изменяющихся от начального до конечного на величину постоянного шага

Дискретной называется переменная, содержащая несколько значений, изменяющихся от начального до конечного на величину постоянного шага. Дискретная переменная может быть задана двумя способами:

1) а := а1, а2 .. an

2)а := а1 .. an

где a– имя дискретной переменной,

a1– ее начальное значение,

a2– ее второе значение,

an – ее конечное значение.

Символ «..»набирается либо клавишей «;» на клавиатуре, либо кнопкой m..n – в палитре матриц.

Для первого способа задания дискретной переменной шаг ее изменения равен (а2 – а1). Для второго способа задания дискретных переменных значение а2 не указывается, шаг изменения дискретной переменной равен 1, если a1<an, или -1, если a1>an.

Примеры создания дискретных переменных приведены ниже.

x:= 2.. 7	Создается дискретная переменная х, значения которой изменяются от 2 до 7 с шагом 1.
y:= 2,2.3.. 7	Создается дискретная переменная y, значения которой изменяются от 2 до 7 с шагом 0.3.
z:= 9 .. 1	Создается дискретная переменная z, значения которой изменяются от 9 до 1 с шагом -1.
a:= 8,7.9.. 3	Создается дискретная переменная a, значения которой изменяются от 8 до 3 с шагом -0.1.
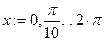
	Создается дискретная переменная b, значения которой изменяются от 0 до 2π с шагом π/10.

Дискретные переменные могут являться аргументами функций, тогда процесс вычисления значений функции приобретает циклический характер, и для каждого значения дискретной переменной вычисляется свое значение функции по заданной аналитической зависимости.

В системе MathCAD в основном используются массивы двух типов: одномерные (векторы) и двумерные (матрицы).

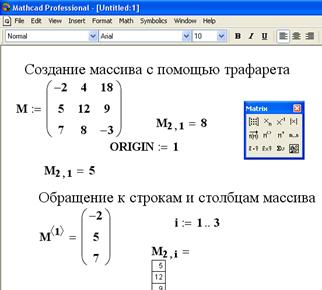
Каждый элемент вектора или матрицы имеет порядковый номер в массиве. Отсчет номеров начинается с того значения, которое содержится в системной переменной ORIGIN. По умолчанию эта переменная имеет значение 0, для изменения значения нужно задать, например,

ORIGIN:=1

Векторы и матрицы можно задавать различными способами: с помощью кнопки с изображением матриц на наборной панели математических инструментов; как переменную с индексами перечислением элементов массива с разделение запятой; с помощью аналитического выражения.

Массивы могут использоваться в выражениях целиком или поэлементно. Для обращения к элементам массивов нужно указать числовые значения индексов элементов в подстрочнике после имени массива. При выполнении расчетов можно обращаться к конкретной строке или столбцу матрицы с помощью верхнего индекса или нижних индексов.

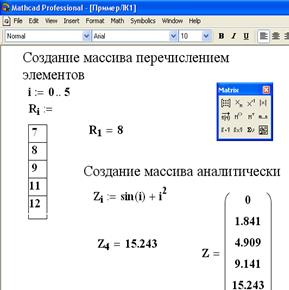
На рисунке 2.2.1 приведены примеры создания массивов перечислением элементов (вектор R) и аналитически (вектор Z). Здесь же показано, как обратиться к элементу матрицы, ее столбцу или строке. Из рисунка видно, что после изменения значения переменной ORIGIN, значение элемента матрицы M_2,1 тоже изменяется.

Рисунок 2.2.1 – Примеры создания массивов

Существует ряд операций над матрицами и векторами, а также встроенных векторных и матричных функций. Введем следующие обозначения: V – вектор, M – матрица. Основные операции с их назначением и правилами набора приведены в таблице 2.2.1.

Таблица 2.2.1. – Основные операции и функции для обработки массивов

Вид операции	Назначение	Набор
|М|	определитель матрицы
М-1	обращение матрицы
МТ	транспонирование матрицы
М< >	выделение столбца матрицы
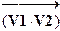
	поэлементное умножение векторов
M∙V	умножение матрицы на вектор	Знак умножения набирается с палитры арифметических операторов
М1·М2	умножение двух матриц
V1∙V2	умножение двух векторов
max(M), min(M)	максимум, минимум матрицы	Стандартные функции набираются с клавиатуры или с использованием мастера функций
cols(M), rows(M)	число столбцов и строк матрицы