Сельскохозяйственного предприятия
| Элементы структуры: виды сельхозструктур | Доли в итоге | ранги | d1j -d0j | (R1j-Roj)2 | ||
| ба-зисн. d0j | текущ. d1j | R0j | R1j | |||
| Пшеница озимая Пшеница яровая Рожь Овес Картофель | 0,25 0,20 0,10 0,05 | 0,15 0,30 0,18 0,04 | l | 0,10 0,30 0,20 0,08 0,01 | ||
| Многолетние травы на сено | 0,22 | 0,27 | 0,05 | |||
| Лен | 0,04 | 0,06 | 0,02 | |||
| Однолетние травы на сено | 0,14 | 0,14 | ||||
| Итого | 0,90 |
Для построения рангового коэффициента логично будет условиться приписать нулевым значениям элементов последние по порядку ранги, если таких элементов несколько - в порядке их рангов в другом периоде. Тогда получим:
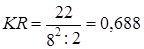 или 68,8% максимального.
или 68,8% максимального.
Квадратический коэффициент интенсивности изменения рангов:
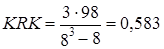 или 58,3% максимального значения.
или 58,3% максимального значения.
Все три показателя указывают на сильный количественный сдвиг в структуре. Но в отличие от ранее рассмотренных примеров, в данном примере нельзя этим ограничиться. Произошло качественное обновление структуры, состава сельскохозяйственных культур, и это качественное изменение отразится следующими показателями:
1. Показатель обновления по числу элементов структуры - отношение числа выбывших и числа новых элементов структуры к общему числу имевшихся разных элементов за оба периода, его можно назвать «коэффициентом обновления состава»:
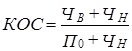 или
или 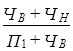 , (11.12)
, (11.12)
где ЧВ, ЧН - число выбывших и число новых элементов:
П0 и П1 - число элементов базисной и текущей структуры.
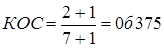 или 37,5% предельной величины.
или 37,5% предельной величины.
2. Принимая во внимание не только число обновившихся элементов структуры, но и их доли, т. е. значение в системе, получим отношение суммы обновившихся долей к максимальной сумме, как уже известно, равной двум целым. Этот показатель назовем «коэффициентом обновления долей»
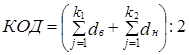 ,
,
где dВ, dН - выбывшие и новые доли;
к1 и к2 - их число.
В данном примере имеем:
КОД (0,14 + 0,20 +0,30) : 2 = 0,32 или 32% максимального показателя.
При полном обновлении всех элементов структуры оба коэффициента обновления равны единице или 100%, так как числа выбывших и новых элементов равны в сумме числам прежних и новых элементов, а суммы выбывших долей и новых долей дают в числителе показателя КОД 2, и 2 в знаменателе. При отсутствии качественного обновления элементов структуры оба коэффициента, естественно, равны нулю, хотя количественный сдвиг может быть очень велик. Например, если при 20 элементах структуры 10 элементов имели по 0,01 и 10 элементов по 0,09, а в следующем периоде размеры их полностью поменяются, то абсолютный показатель интенсивности структурного сдвига достигнет (10∙0,08 + 10∙0,08) : 2 = 0,8 или 80% максимального. Напротив, при сильном качественном обновлении, например, 18 элементов структуры из 20, если сумма долей этих обновившихся элементов составляет всего 0,18, а 2 доли, составляющие в сумме 0,82, остались неизменными, то количественные меры структурного сдвига окажутся низкими, хотя коэффициент обновления достигает по числу элементов: КОС = 18 : 20 = 0,9 или 90% максимального.
Приведенные примеры показывают, что при анализе изменения структуры следует применить не какой-то один показатель, а всю их систему, так как каждый показатель отражает, измеряет особый аспект структурного сдвига. Разные показатели изменения структуры связаны между собой не жесткой связью, а связью статистической, в среднем - прямой зависимостью, но в конкретных процессах изменения структуры разные показатели могут сильно расходиться и даже изменяться в разных направлениях.
Изменение структуры сложных систем включает не только изменение состава и долей материальных элементов структуры, но также изменение структуры связей между этими элементами. Об изучении структуры связей, в частности, коэффициента детерминации при многофакторной регрессии см. гл. 8.
Рекомендуемая литература к главе 11
1. Агапова Т. Н. Методы статистического изучения структуры сложных систем и ее изменения. - М.: Финансы и статистика, 1996.
2. Казинец Л. С. Измерение структурных сдвигов в экономике. - М.: Экономика, 1969.
3. Казинец Л. С. Темпы роста и структурные сдвиги в экономике. - М.: Экономика, 1981.
4. Гатев К. Статистическая оценка различий между структурами / Теоретические и методологические проблемы статистики / М., Статистика, 1979.
5. Елисеева И. И., Рукавишников В. Н. Группировка, корреляция, распознавание образов. - М.: Статистика, 1977.
6. Миркин Б. Г. Анализ качественных признаков и структур. - М.: Статистика, 1980.
Дата добавления: 2015-01-21; просмотров: 762;
