И колеблемости

Прогнозирование возможных в будущем значений признаков изучаемого объекта - одна и основных задач науки. В ее решении роль статистических методов очень значительна. Одним из статистических методов прогнозирования является расчет прогнозов на основе тренда и колеблемости динамического ряда до настоящего времени. Если мы будем знать, как быстро и в каком направлении изменились уровни какого-то признака, то сможем узнать, какого значения достигнет уровень через известное время. Методика статистического прогноза по тренду и колеблемости основана на их экстраполяции, т.е. на предположении, что параметры тренда и колебаний сохраняются до прогнозируемого периода. Такая экстраполяция справедлива, если система развивается эволюционно в достаточно стабильных условиях. Чем крупнее система, тем более вероятно сохранение параметров ее изменения, конечно, на срок не слишком большой! Обычно рекомендуют, чтобы срок прогноза не превышал одной трети длительности базы расчета тренда.

В отличие от прогноза на основе регрессионного уравнения прогноз по тренду учитывает факторы развития только в неявном виде, и это не позволяет «проигрывать» разные варианты прогнозов при разных возможных значениях факторов, влияющих на изучаемый признак. Зато прогноз по тренду охватывает все факторы, в то время как в регрессионную модель невозможно включить в явном виде более 10-20 факторов в самом лучшем случае.

Сущность прогноза на основе тренда хорошо иллюстрируется следующим рассказом о греческом философе Диогене, жившем в большой бочке на берегу Саронического залива недалеко от афинского порта Пирея. Как-то вечером Диогена стал окликать снаружи неизвестный. Диоген вышел в нему. - «Скажи, мудрый человек», -спросил путник, - дойду ли я к закату в Афины?» Диоген посмотрел на него и сказал: - «Иди!» Путник повторил свой вопрос... -«Иди!» - закричал Диоген, и путник, пожав плечами, побрел по берегу. - «Вернись!» - снова закричал Диоген, и путник вернулся к нему. - «Вот теперь я тебе скажу, что до заката ты не дойдешь до Афин. Оставайся у меня». - «А почему же ты сразу мне это не сказал, а прогнал меня?» Диоген усмехнулся: - «А как же я скажу, дойдешь ли ты до Афин, если я не видел, как быстро ты ходишь?» Прогноз по тренду - это и есть Диогенов прогноз на основании знания того, как изучаемая система «шла» до настоящего времени.

Рассмотрим методику прогнозирования по тренду с учетом колеблемости на примере цен на нетопливные товары развивающихся стран, тренд и колеблемость которых была измерена в параграфах 9.6 и 9.7 (табл. 9.4 и 9.7). За основу прогнозов возьмем параметры, полученные методом многократного скользящего выравнивания. Параллельно будет показана и методика расчетов при однократном выравнивании.

Итак, имеем уравнение тренда у̂ = 104,53 - 1,433t, где t =0 в 1987 г., оценку генеральной величины среднего квадратического отклонения от тренда s(t) = 9,45. Эти значения получены при анализе динамики цен весьма значительного сектора мировой торговли, т. е. очень большой и сложной системы. Маловероятно, что условия развития этой системы существенно изменятся, скажем, до 1998 г. Поэтому, прогноз на 1998 г. по измеренному тренду можно теоретически считать достаточно обоснованным. Обычно рекомендуется, чтобы период упреждения (от конца базы расчета до прогнозируемого периода) составлял не более трети длины базы расчета.

Прежде всего, вычисляется «точечный прогноз» - значение уровня тренда при подстановке в его уравнение номера 1998 г., считая от 1987 г., т.е. t_k = 11.

ŷ₁₉₈₈ = 104,53 - 1, 433·11 = 88,77.

Это означает, что наиболее вероятное значение индекса цен на нетопливные товары развивающихся стран в 1998 г. составит около 89% к уровню цен 1990 г., принятому за 100%. Однако, параметры тренда, полученные по ограниченному числу уровней ряда - это лишь выборочные средние оценки, не свободные от влияния распределения колебаний отдельных уровней во времени, как уже сказано ранее. При изменении базы расчета тренда, если, скажем взять 1977 - 1993 гг. или 1981—1997 гг., были бы получены несколько иные значения параметров, а значит, и другие значения ŷ₁₉₈₈. Прогноз должен иметь вероятностную форму, как всякое суждение о будущем.

Средняя ошибка прогноза положения линейного треида на год (момент) с номером t_k вычисляется по формулам:

А) • Для однократного выравнивания:

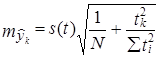(9.48)

где t_k - номер года прогноза,

S_ti² - по всей длине ряда N, т. е. .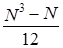

Б) • Для многократного скользящего выравнивания При/сдвигах базы и длине ее n:

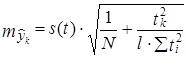(9.49)

где .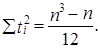

При N = 17, п = 11, l = 7 получаем:

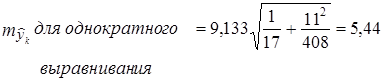
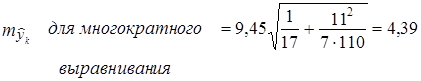
Как видим, метод многократного выравнивания на 20% снизил среднюю ошибку прогноза положения тренда.

Для получения достаточно надежных границ прогноза положения тренда, скажем, с вероятностью 0,9 того, что ошибка будет не более указанной, следует среднюю ошибку умножить на величину t-критерия Стьюдента при указанной вероятности (или значимости 1 - 0,9 = 0,1) и при числе степеней свободы, равном, для линейного тренда, N - 2, т.е. 15. Эта величина равна 1,753. Получаем предельную с данной вероятностью ошибку

4,39 • 1,753 = 7,70.

Следовательно, с вероятностью 0,9 можно ожидать, что тренд индекса цен в 1988 г. пройдет между значениями ŷ_1998+a и ŷ_1998-a,т.е. 88,77 + 7,70 и 88,77 - 7,70; от 81,07 до 96,47 в процентах к уровню цен 1990 г. и, конечно, в одинаковой валюте, без учета ее инфляции.

Однако, фактические уровни ряда отклоняются от тренда. Уровень цен в 1998 г. также может быть вовсе не равен уровню положения тренда в этом году. Ошибка прогноза конкретного уровня включает две неопределенности: во-первых, мы не знаем точно, где окажется тренд в 1998 г., а во-вторых - в какую сторону и на сколько уровень ряда отклонится в 1998 г. от положения тренда. Считая, как уже было сказано, колебания случайно (в основном, случайно) распределенными во времени, т. е. независимыми от тренда, определим ошибку прогноза уровня конкретного года по правилу сложения независимых дисперсий.

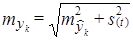(9.50)

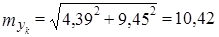
С вероятностью 0,9 ошибка прогноза уровня цен не превзойдет величины 18,27 (10,42·1,753) и доверительные границы прогноза. составят от 70,5 до 107,0% к уровню 1990 г. Как видим, точность прогноза, невелика, разброс возможных значений достиг 37 пунктов, а вероятная ошибка составила 0,206 или 20,6% 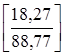от средней величины (точечного прогноза). Можно уменьшить значение, вероятной ошибки, если сделать прогноз с меньшей надежностью, скажем, с вероятностью 0,75. Тогда значение t-критерия Стьюдента составит 1,197, вероятная ошибка составит 12,47 пункта, [10,42·1,197] доверительные границы - от 76,30 до 101,24 % к уровню 1990 г. За уменьшение вероятной ошибки, однако, пришлось заплатить снижением надежности прогноза.

Из имеющейся информации нельзя извлечь больше, чем в ней содержится: как в физике действует закон сохранения массы и энергии, импульса («количества движения»), так здесь действует закон сохранения информации: увеличивая точность, мы понижаем надежность, увеличивая надежность - понижаем точность. Методика анализа и прогнозирования тоже имеет значение. Она определяет степень полноты извлечения информации, содержащейся в исходном ряду динамики. С помощью методики многократного выравнивания удается более полно извлечь информацию о тренде и уменьшить среднюю ошибку прогноза его положения в прогнозируемом периоде с 5,44 до 4,39. Однако, как видно из (9.50), главной составляющей ошибки прогноза конкретного уровня в нашем расчете является не ошибка прогноза положения тренда, а колеблемость уровней около тренда. Поэтому ошибка прогноза конкретного уровня незначительно сократилась за счет многократного выравнивания. При слабой колеблемости уровней и прогнозировании на значительное удаление от базы, главную роль станет играть ошибка положения тренда. Тогда многократное выравнивание даст значительное сокращение средней ошибки прогноза конкретных уровней. Но в любом случае эта ошибка всегда больше показателя колеблемости уровней - среднего квадратического отклонения S_y(t)[13] . В частности, в указанной литературе содержатся формулы для вычисления средней ошибки прогноза положения линии тренда при параболической и экспоненциальной его формах[14]. Если средняя ошибка положения тренда вычислена, ошибку конкретного уровня при любой форме тренда вычисляют по формуле (9.50).