Сезонность смертности в Санкт-Петербурге
| Месяц | Число умершших в среднем за сутки | В % к среднемесячному показателю | Отклонения от средней, yi - y̅ | (yi - y̅)2 | |||
| в среднем за 3 года | |||||||
| Январь | 246,8 | 229,5 | 243,0 | 239,8 | 114,8 | 31,0 | 961,00 |
| Февраль | 258,9 | 212,3 | 209,7 | 227,0 | 108,7 | 18,2 | 331,24 |
| Март | 225,5 | 220,7 | 187,6 | 211,3 | 101,2 | 2,5 | 6,25 |
| Апрель | 211,9 | 212,3 | 182,8 | 202,3 | 96,9 | -7,2 | 51,84 |
| Май | 231,0 | 208,7 | 180,6 | 206,8 | 99,0 | -2,0 | 4,00 |
| Июнь | 235,4 | 205,7 | 173,1 | 204,7 | 98,0 | -4,1 | 16,81 |
| Июль | 227,4 | 211,3 | 181,8 | 206,8 | 99,0 | -2,0 | 4,00 |
| Август | 220,6 | 204,5 | 171,4 | 198,8 | 95,2 | -10,0 | 100,00 |
| Сентябрь | 233,5 | 193,0 | 178,8 | 201,8 | 96,6 | -7,0 | 49,00 |
| Октябрь | 229,3 | 196,0 | 186,5 | 203,9 | 97,7 | -4,9 | 24,01 |
| Ноябрь | 212,5 | 196,7 | 170,4 | 193,2 | 92,5 | -15,6 | 243,36 |
| Декабрь | 218,3 | 228,6 | 181,5 | 209,5 | 100,3 | 0,7 | 0,49 |
| Средняя | 229,1 | 210,0 | 187,3 | 208,8 | 100,0 | - | 1792,24 |
Наиболее точную и полную методику анализа с разложением ряда динамики на три компонента: тренд, сезонную колеблемость и случайную колеблемость рассмотрим на примере динамики импорта КНР по кварталам за 1993 - 1995 гг. (табл. 9.10).
Анализ в табл. 9.10 проводится по следующей методике:
1. По месячным или квартальным данным за все годы вычисляется уравнение тренда и выравненные по нему уровни, обозначаемые у̂ij, где i - номер года; j - номер квартала или месяца.
2. Каждый фактический уровень делится на соответствующий выравненный для расчета индексов сезонности Сij.
3. Индексы сезонности усредняются за все годы, получаем средние индексы сезонности для каждого квартала или месяца:
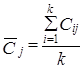 (9.39)
(9.39)
где i - номер года;
k - число лет;
j - номер квартала, месяца.
 4. Выравненные уровни умножаются на средние индексы сезонности для соответствующих кварталов или месяцев, получаем выравненные уровни с учетом сезонности y̅'ij
4. Выравненные уровни умножаются на средние индексы сезонности для соответствующих кварталов или месяцев, получаем выравненные уровни с учетом сезонности y̅'ij
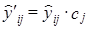 (9.40)
(9.40)
5. Вычисляются отклонения (и их квадраты) за счет сезонности:
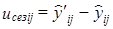 (9.41)
(9.41)
6. Вычисляются отклонения (и их квадраты) за счет случайной колеблемости:
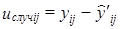 (9.42)
(9.42)
7. Вычисляются общие отклонения:
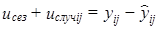 (9.43)
(9.43)
Уровни в табл. 9.10 - это объем импорта в КНР по кварталам (в ценах fob, т. е. «franco board» - с учетом затрат на погрузку на борт корабля или в вагоны, на грузовики, но не включая стоимость перевозки, фрахта)[12].
Прежде всего отметим, что при наличии существенных сезонных колебаний параметры тренда будут вычислены правильно только при условии, что первый и конечный уровни относятся к одному и тому же кварталу (месяцу), иначе сезонность исказит параметры тренда. Поэтому, в расчет включаем и I квартал 1996 г.
Графическое изображение динамического ряда с наличием сезонных колебаний возможно двумя способами.Первый способ - обычная линейная диаграмма в декартовой системе координат, аналогичная рис. 9.3
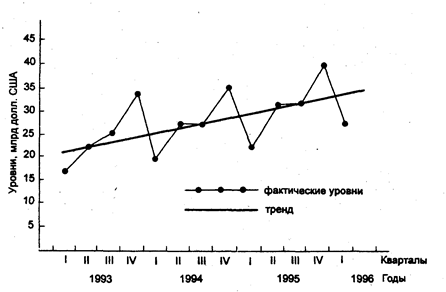
Рис. 9.3. Динамика импорта КНР, млрд долл. США
.
Второй способ - изображение в полярных координатах. Величина уровня изображается расстоянием от центра, между месяцами угол 30°, между кварталами - 90°. График имеет вид разворачивающейся спирали, если тренд направлен к возрастанию, и сворачивающейся, если тренд направлен к уменьшению уровней. Сезонные колебания выражены тем, что точки четвертых кварталов далеко выходят за окружность, радиус которой - средний уровень 1993 г., а точки первых кварталов - внутри нее (рис. 9.4).
Средний уровень ряда
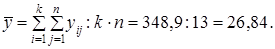
Тренд имеет линейную форму со среднегодовым абсолютным приростом
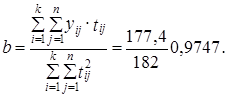

Рис. 9.4, Сезонность импорта КНР, млрд долл. США
Средние индексы сезонности за 3 года (для 1 квартала - за 4 года) составляют:
| Квартал | Ci |
| I | 0,7678 |
| II | 1,0011 |
| III | 1,0294 |
| IV | 1,2759 |
Таким образом, наблюдается сезонный спад импорта в I квартале на 23 с лишним процента и подъем в конце года, а уровни II и III кварталов почти равны средним квартальным значениям. Такая форма сезонных колебаний весьма далека от плавной синусоидальной кривой и к ней неприменима модель тригонометрического вида:
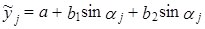 ,
,
где aj - угол, изменяющийся от 0° в начале года до 360° в конце, т. е. на 30° на месяц или на 90° за квартал.
Методика, изложенная выше, имеет более общий характер, и при наличии достаточно дробной по частям года информации, может быть использована для моделирования сезонных колебаний любых форм, в том числе с разными «пиками» и «провалами». Следует, однако, учитывать, что чем более дробные единицы времени охватывает информация, тем больше к сезонным колебаниям примешиваются случайные или связанные с недельным трудовым циклом колебания.
При изучении торговых операций или работы транспорта, особенно в крупных городах, следует изучать и измерять даже внутри-суточную колеблемость продажи или пассажиропотоков так как важно знать распределение во времени и величину «пиковых нагрузок». При изучении внутрисуточной колеблемости, как правило, можно пренебречь трендом и применять более простую методику, изложенную в начале данного раздела, усреднив почасовые данные за все рабочие дни недели.
Общую дисперсию уровней динамического ряда, измеряемую суммой квадратов отклонений этих уровней от их средней величины 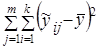 можно разложить на составляющие:
можно разложить на составляющие:
1. Дисперсия за счет тренда:
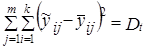 (9.44)
(9.44)
2. Дисперсия за счет сезонных колебаний:
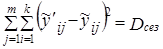 (9.45)
(9.45)
3. Дисперсия за счет. случайных колебаний (остаточная):
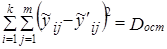 (9.46)
(9.46)

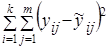 (9.47)
(9.47)
По данным табл. 9.9 имеем:
общую дисперсия уровней, равную 480,4;
дисперсию за счет тренда, которая составляет 168,1;
дисперсию за счет сезонности 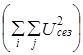 =389,3;
=389,3;
случайную дисперсию  =18,4;
=18,4;
дисперсию случайную + дисперсию сезонную:
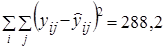
Легко заметить, что сумма составляющих дисперсий больше общей дисперсии, что кажется ошибкой. На самом деле, однако, нужно учесть, чтоколебания - величина не скалярная, а векторная, т. е. имеет не только размер, но и направление, знак. Тренд отделен от колебаний, а все случайные и сезонные колебания могут иметь и совпадающие и несовпадающие знаки, т. е. они могут частично погашать друг друга, что имеет место особенно в конце изучаемого периода. Поэтому общая колеблемость, измеряемая суммой квадратов отклонений (9.47) значительно меньше, чем сумма дисперсий за счет сезонной и случайной колеблемости. По данным табл. 9.10 общая колеблемость составила 288,2. Находим отношение этой величины к сумме сезонной и случайной дисперсий:
288,2 : (389,3 + 18,4) = 0,70706.
На эту величину корректируем сезонную и случайную суммы квадратов отклонений и окончательно получаем следующее разложение общей дисперсии уровней ряда (табл. 9.11)
Из табл. 9.11 следует ряд выводов: основным источником различия квартальных уровней импорта КНР за изучаемый период времени являлась сезонная колеблемость. Случайная колеблемость существенной роли не играла. Проверка существенности различий по критерию Фишера показала, что и тренд и сезонная колеблемость существенны, как и различия уровней в целом. Табличное значение F в несколько раз меньше фактических, так что вероятность существенности различий много ближе к единице, чем к 0,95, для которой приведены табличные значения F. Отметим, что при изучении сезонных колебаний по месячным уровням, сезонная дисперсия будет иметь (12-1) степень свободы. Сумма степеней свободы сезонной и случайной дисперсий равна числу уровней ряда за вычетом числа параметров тренда.
Таблица 9.11
Дата добавления: 2015-01-21; просмотров: 1190;
