Проверка гипотезы о линейном тренде индекса цен

(1990 г. = 100%)

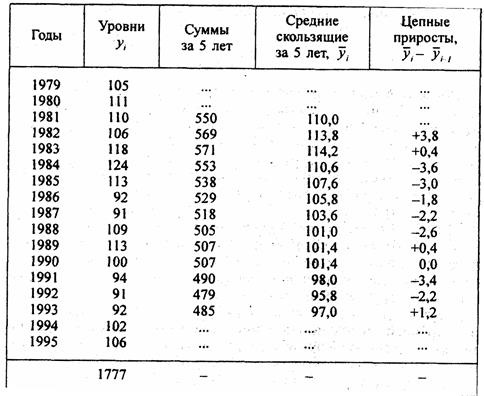
В первую очередь проверяется гипотеза о наиболее простой - линейной форме уравнения тренда, т. е. о несущественности различий цепных абсолютных изменений. Имеем 12 абсолютных изменений скользящей средней, которая хотя и сгладила сильные колебания уровней ряда, но как видим, ее абсолютные изменения далеко не одинаковы. Разбиваем эти 12 цепных приростов на два подпериода: по 6 приростов в каждом, и для каждого подпериода вычисляем среднюю Δ̅_k среднее квадрагическое отклонение (СКО) как оценку генерального СКО с учетом потери одной степени свободы вариации, s

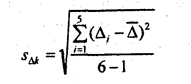
и среднюю ошибку среднего изменения т_Δk по правилам, рассмотренным в главе 7:

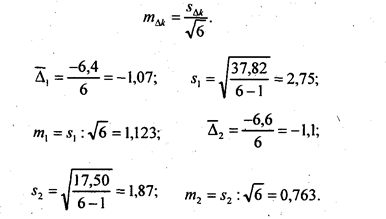
Для проверки гипотезы о несущественности различий между средними абсолютными изменениями по подпериодам Δ̅₁, Δ̅₂. М. С. Каяйкина предложила проверять существенность их различий попарно по t-критерию Стьюдента. Затем методика была дополнена и усовершенствована А. И. Манеллей, предложившим проверять существенность всех различий сразу по критерию Фишера.

Средняя случайная ошибка разностей двух выборочных средних оценок, как показано в гл. 7, есть корень квадратный из суммы квадратов ошибок каждой из средних, т. е.

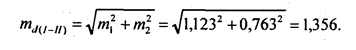
Критерий Стьюдента для существенности различия двух среднегодовых приростов (изменений) составит:

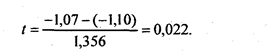
Критическое значение критерия при уровне значимости 0,05 и при (6-1) + (6-1) = 10 степенях свободы равно 2,23 (см. Приложение 2). Фактическое значение много меньше. Следовательно вероятность того, что различие среднегодовых приростов в разные под-периоды случайно, превышает 0,05 и гипотеза о равенстве приростов не отклоняется. А значит, тенденцию динамики на реем протяжении ряда можно считать линейной.

Если же гипотеза о линейности отклоняется, по скользящим средним и их цепным приростам вычисляют ускорения приростов и аналогичным методом проверяют существенность различия ускорения в подпериодах. Если несущественно различиеускорений, принимается гипотеза о том, что тренд - парабола II порядка. Если и гипотеза о постоянстве ускорений отклоняется, то по скользящей средней вычисляют цепные темпы роста и проверяют гипотезу об их постоянстве по подпериодам. Подтверждение (неотклонение) этой гипотезы означает принятие гипотезы о том, что тренд экспоненциальный.

Проверка гипотез о других типах тенденций динамики, рассмотренных в п. 9.4, сложнее и здесь излагаться не будет. Итак, в нашем примере принято решение считать тренд линейным, и следует приступить к вычислению его параметров.