Итерационные методы решения систем линейных уравнений
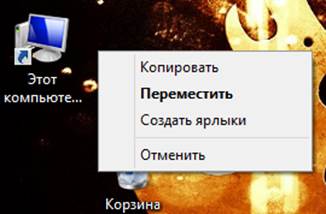
Меню специального перетаскивания. Наведите указатель мыши на значок Мой компьютер, нажмите правую кнопку мыши и, не отпуская ее, переместите мышь. Отпустите кнопку – откроется так называемое меню специального перетаскивания. Для большинства объектов это меню содержит пункты: Копировать, Переместить, Создать ярлык и Отменить. Для особых объектов, таких как Мой компьютер, Корзина и др., меню содержит пункты: Создать ярлык и Отменить. Выберите пункт Отменить и нажмите левую кнопку мыши.
Контрольные вопросы.
1. Каким образом можно получить всплывающую подсказку?
Задержав курсор на объекте
2. Как развернуть окно MS-DOS на весь экран?
Нажать Alt+Tab
3. Как правильно произвести двойной щелчок?
Быстро нажать 2 раза левой кнопкой мыши на объект
4. Как открыть контекстное меню?
Нажать правую кнопку мыши
5. Как перетащить значок, окно программы в другое место?
Нажать на значок левой кнопкой мыши и не отпуская перетащить в нужное место
6. Каким образом можно выделить группу объектов?
Левым кликом мыши объединить нужные объекты
7. Как производится специальное перетаскивание?
Правым кликом мыши перетащить объект
8. Каковы преимущества специального перетаскивания?
Доступно контекстное меню со специальными функциями
Вывод
Итерационные методы решения систем линейных уравнений
Итерационные методы решения систем линейных уравнений отличаются самоисправляемостью и простотой реализации на ЭВМ. Итерационные методы требуют задания начальных приближений. Сходимость итерационных методов зависит от свойств матрицы системы и выбора начальных приближений.
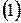 Рассматривается следующая система:
Рассматривается следующая система:
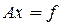 ,
,
где 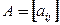
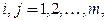
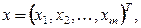
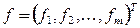 .
.
1. Метод итераций
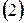 Перед применением метода итераций систему (1) необходимо привести к эквивалентному виду
Перед применением метода итераций систему (1) необходимо привести к эквивалентному виду
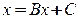 .
.
Метод итераций для системы (2) имеет вид
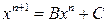 .
.
Теорема.Если 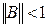 , где
, где 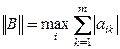 то метод итераций сходится при любом начальном приближении
то метод итераций сходится при любом начальном приближении 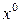 со скоростью геометрической прогрессии.
со скоростью геометрической прогрессии.
В качестве начального приближения обычно выбирается вектор свободных членов 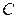 , тогда для оценки числа итераций, необходимых для достижения заданной точности, можно использовать формулу
, тогда для оценки числа итераций, необходимых для достижения заданной точности, можно использовать формулу
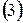
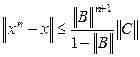
Пример. Методом итераций решить систему линейных уравнений
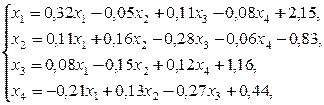
предварительно оценив число необходимых для этого шагов, 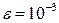 .
.
Число шагов, дающих ответ с точностью до 0,001, определим из соотношения (3). Здесь
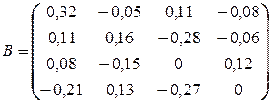 ,
,
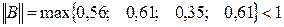 ; значит, итерационный процесс сходится;
; значит, итерационный процесс сходится;
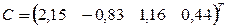 ,
,
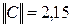 . Имеем
. Имеем
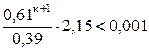 ;
; 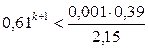 ;
; 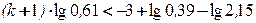 ;
; 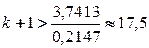 ;
; 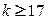 .
.
В качестве нулевого приближения выбираем вектор С.
Вычисления расположим в таблице
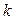
| 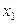
| 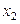
| 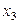
| 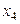
|
| 2,15 | -0,83 | 1,16 | 0,44 | |
| 2,9719 | -1,0775 | 1,5093 | -0,4326 | |
| 3,3555 | -1,0721 | 1,5075 | -0,7317 | |
| 3,5017 | -0,0106 | 1,5015 | -0,8111 | |
| 3,5511 | -0,9277 | 1,4944 | -0,8312 | |
| 3,5637 | -0,9563 | 1,4834 | -0,8298 | |
| 3,5678 | -0,9566 | 1,4890 | -0,8332 | |
| 3,5700 | -0,9575 | 1,4889 | -0,8356 | |
| 3,5709 | -0,9573 | 1,4890 | -0,8362 | |
| 3,5712 | -0,9571 | 1,4889 | -0,8364 | |
| 3,5713 | -0,9570 | 1,4890 | -0,8364 |
2. Метод Якоби
Метод Якоби для системы (1) в координатной форме имеет вид
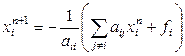 ,
, 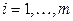
Теорема.Пусть 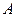 - матрица с диагональным преобладанием, то есть
- матрица с диагональным преобладанием, то есть
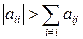 .
.
Тогда метод Якоби сходится.
Если систему (1) представить в виде (2), то можно оценить количество итераций по формуле (3).
Пример. Методом Якоби решить систему линейных уравнений
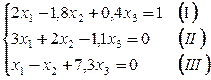
предварительно приведя матрицу системы к матрице с диагональным преобладанием и оценить число необходимых шагов для достижения точности 0,001.
Приведем систему к виду, в котором элементы главной диагонали превосходили бы остальные элементы строк:
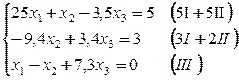
Для оценки числа итераций запишем эту систему в виде (2), поделив каждое уравнение на диагональный элемент:
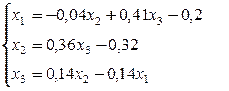
Число шагов, дающих ответ с точностью до 0,001, определяется из соотношения (3). Здесь
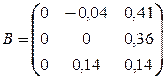 ,
,
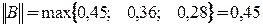 ;
;
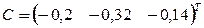 ,
,
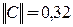 . Имеем
. Имеем
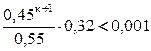 ;
; 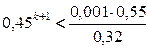 ;
; 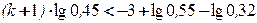 ;
; 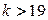 .
.
Нулевое приближение 
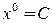 ;
;
Вычислим первое приближение
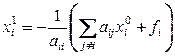
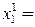
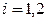
где 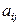 - элементы матрицы
- элементы матрицы
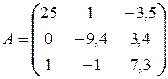 ,
,
а 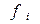 - элементы вектора
- элементы вектора 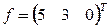 .
.
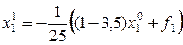 ,
, 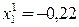 .
.
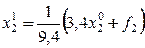 ,
, 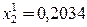 .
.
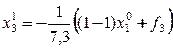 ,
, 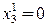 .
.
Для окончания вычислений нужно произвести 20 итераций.
3. Метод простой итерации
Метод простой итерации для системы (1) имеет вид
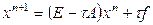
или в канонической форме
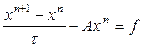 ,
,
где 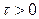 - постоянный итерационный параметр.
- постоянный итерационный параметр.
Теорема.Если 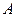 - симметричная положительно определенная матрица, тогда метод простой итерации сходится при
- симметричная положительно определенная матрица, тогда метод простой итерации сходится при 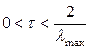 .
.
Теорема.Если 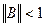 , где
, где 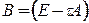 , то метод простой итерации сходится.
, то метод простой итерации сходится.
Пример.Пусть матрица A имеет вид
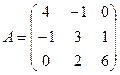 ,
,
тогда
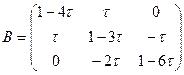 ;
;
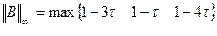 . (складываются модули элементов в каждой строке )
. (складываются модули элементов в каждой строке )
Выберем 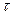 так, чтобы выполнялось условие сходимости
так, чтобы выполнялось условие сходимости 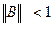 .
.
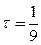 .
.
Число итераций, необходимое для заданной точности, можно вычислить как в случае метода итераций.
4. Метод Зейделя
Итерационный метод Зейделя для системы (1) в координатной форме имеет вид
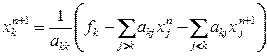 ,
, 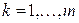
Теорема.Если 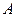 - матрица с диагональным преобладанием, тогда метод Зейделя сходится для любого начального приближения.
- матрица с диагональным преобладанием, тогда метод Зейделя сходится для любого начального приближения.
Теорема.Если 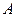 - симметричная положительно определенная матрица, тогда метод Зейделя сходится.
- симметричная положительно определенная матрица, тогда метод Зейделя сходится.
Пример. Методом Зейделя решить с точностью 0,001 систему линейных уравнений
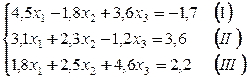 ,
,
приведя ее к виду, удобному для итераций.
Приведем систему к виду, в котором элементы главной диагонали превосходили бы остальные элементы строк
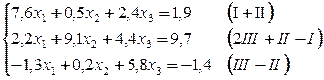
Нулевое приближение 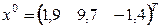 .
.
Первое приближение
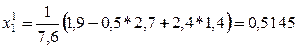
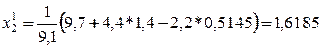
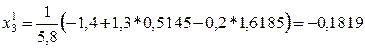
и т.д.
Окончание вычислений определяется условием
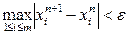 ,
,
где 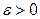 - заданное число.
- заданное число.
5. Метод верхней релаксации
Метод верхней релаксации является обобщением метода Зейделя. В координатной форме метод верхней релаксации имеет следующий вид
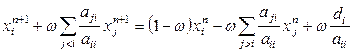 ,
, 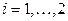
При 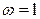 этот метод совпадает с методом Зейделя.
этот метод совпадает с методом Зейделя.
Теорема.Если 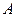 - симметричная положительно определенная матрица, тогда метод верхней релаксации сходится при
- симметричная положительно определенная матрица, тогда метод верхней релаксации сходится при 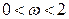 .
.
Окончание вычислений определяется условием
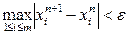 ,
,
где 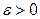 - заданное число.
- заданное число.
6. Метод минимальных невязок
Метод минимальных невязок определен для систем уравнений с симметричной положительно определенной матрицей 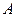 . Этот метод определяется формулой
. Этот метод определяется формулой
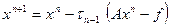 , (4)
, (4)
где параметр 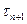 выбирается из условия минимума
выбирается из условия минимума 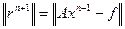 при заданной норме
при заданной норме 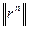 :
:
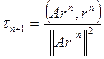 ,
, 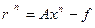
Теорема.Если 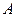 - симметричная положительно определенная матрица, тогда метод минимальных невязок сходится.
- симметричная положительно определенная матрица, тогда метод минимальных невязок сходится.
Окончание вычислений определяется условием
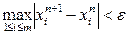 ,
,
где 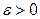 - заданное число.
- заданное число.
7. Метод скорейшего спуска
Если в формуле (4) итерационный параметр 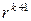 выбирается из условия минимума
выбирается из условия минимума 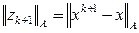 , где
, где 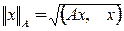 при заданном
при заданном 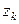 , то этот метод называется методом скорейшего спуска. Итерационные параметры вычисляются по формуле
, то этот метод называется методом скорейшего спуска. Итерационные параметры вычисляются по формуле
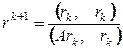 ,
, 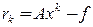 .
.
Теорема.Пусть А – симметричная положительно определенная матрица, тогда метод скорейшего спуска сходится.
Окончание вычислений определяется условием
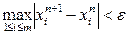 ,
,
где 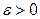 - заданное число.
- заданное число.
Задачи
Методом итераций решить системы линейных уравнений, предварительно приведя их к виду, удобному для итераций и оценив число необходимых для этого шагов, 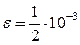 .
.
№ 1.
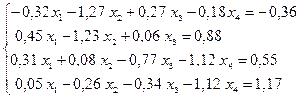
№ 2.
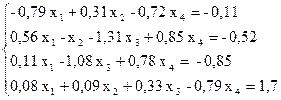
№ 3.
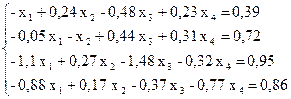
№ 4.
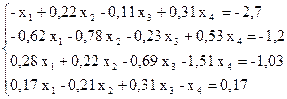
Методом Якоби решить системы линейных уравнений, предварительно приведя матрицу системы к матрице с диагональным преобладанием и оценив число необходимых шагов для достижения точности 0,001.
№ 5.
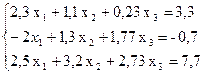
№ 6.
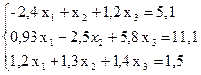
№ 7.
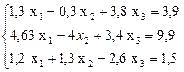
№ 8.
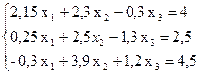
Методом простой итерации решить систему линейных уравнений с точностью до 0,001.
№ 9.
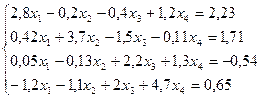
№ 10.
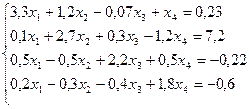
№ 11.
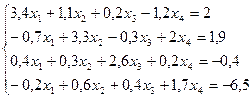
№ 12.
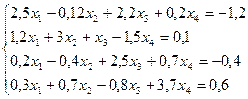
Методом Зейделя решить системы линейных уравнений, приведя их к виду, удобному для итераций, 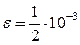 .
.
№ 13.
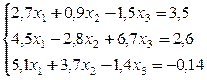
№ 14.
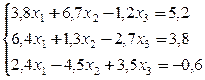
№ 15.
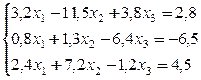
№ 16.
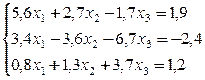
Методом верхней релаксации решить системы линейных уравнений, приведя их к виду, удобному для итераций, 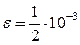 .
.
№ 17.
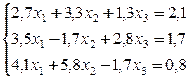
№ 18.
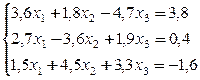
№ 19.
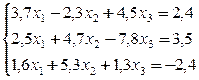
№ 20.
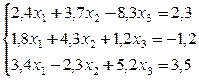
Решить системы линейных уравнений методом минимальных невязок и методом скорейшего спуска, 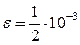 .
.
№ 21.
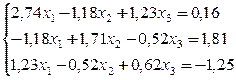
№ 22.
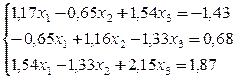
№ 23.
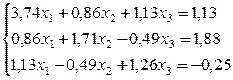
№ 24.
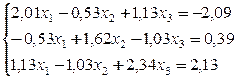
Дата добавления: 2015-01-09; просмотров: 6631;
