Теоретико-множественные отношения
1. Объединение
Объединение двух отношений R1 и R2 определяет новое отношение, содержащее множество кортежей, принадлежащих либо первому R1, либо второму R2 исходным отношениям, либо обоим отношениям одновременно. При этом отношения R1 и R2 должны быть совместимы по объединению.
Таблица 4 - Отношение R1, исходное для операции объединения
| R1 – Поставщик | |
| Код города | Город |
| Тольятти | |
| Москва | |
| Пенза | |
| Тверь |
Таблица 5 - Отношение R2, исходное для операции объединения
| R2 – Потребитель | |
| Код города | Город |
| Тольятти | |
| Саратов | |
| Пенза | |
| Сызрань |
Пример: Показать города поставщиков и потребителей продукции. Исходные данные отображены в таблицах 4 и таблице 5, результат объединения указан в таблице 6.
SELECT Город
FROM Поставщик
UNION
SELECT Город
FROM Потребитель
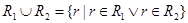 ,
,
где 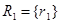 ,
, 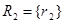 - отношения;
- отношения;
r1 и r2 соответственно кортежи отношений R1 и R2;
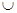 - знак объединения;
- знак объединения;
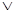 - операция логического сложения «ИЛИ».
- операция логического сложения «ИЛИ».
Таблица 6 - Отношение R3, результат объединения
| R3 – объединение (города поставщиков и потребителей.) | |
| Код города | Город |
| Тольятти | |
| Москва | |
| Саратов | |
| Пенза | |
| Тверь | |
| Сызрань |
2 Пересечение
Пересечение двух отношений R1 и R2 называется новым отношением, которое содержит множество кортежей, принадлежащих и первому R1 и второму отношению R2.
Пример. Показать города, которые являются одновременно и городами поставщиков и городами потребителей продукции. Исходные данные отображены в таблицах 4 и 5, результат пересечения указан в таблице 7.
SELECT Город
FROM Поставщик
INTERSECT
SELECT Город
FROM Потребитель;
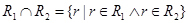 ,
,
где 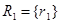 ,
, 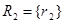 - отношения;
- отношения;
r1 и r2 соответственно кортежи отношений R1 и R2;
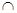 - знак пересечения;
- знак пересечения;
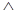 - операция логического сложения «И».
- операция логического сложения «И».
Таблица 7 - Отношение R4 результат пересечения
| R4 – пересечение (города одновременно поставщиков и потребителей) | |
| Код города | Город |
| Тольятти | |
| Пенза |
3. Разность
Разностью отношений называется отношение, содержащее множество кортежей, принадлежащих R1 и не принадлежащих R2 (и наоборот).
Пример: Показать города, которые являются городами поставщиков, но не являются городами потребителей продукции. Исходные данные отображены в таблицах 4 и 5, результат разности указан в таблице 8.
SELECT Город
FROM Поставщик
EXCEPT
SELECT Город
FROM Потребитель;
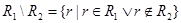 ,
,
Таблица 8 - Отношение R5 результат разности
| R5 – разность (города поставщиков без городов потребителей) | |
| Код города | Название |
| Москва | |
| Тверь |
4. Декартово произведение
Введем предварительно понятие конкатенации.
Конкатенацией, или сцеплением кортежей с = <d, с2…сп> и q = <q1, q2, …qm>, называется кортеж, полученный добавлением значений второго в конец первого:
<с, q> = < d, c2,…cn, qiT q2,…qm>-
Операция декартово произведение определяет новое отношение, которое является результатом конкатенации (т.е. сцепления) каждого кортежа из отношения R7 с каждым кортежем из отношения R8.
Пример: Показать всех сотрудников, участвующих в проектах, с названиями этих проектов, с условием, что каждый сотрудник участвует в каждом проекте. Исходные данные отображены в таблицах 9 и 10, результат объединения указан в таблице 11.
SELECT *
FROM Сотрудники CROSS JOIN Проекта;
или
SELECT *
FROM Сотрудники, Проекта;
Таблица 9 - Отношение R7, исходное для операции декартово произведение (таблица Сотрудники)
| R7 – информация о сотрудниках | |||
| Код сотрудника | Фамилия | Имя | Отчество |
| Иванов | Юрий | Игоревич | |
| Орлов | Егор | Петрович | |
| Юрков | Павел | Антонович | |
| Степанов | Олег | Сергеевич | |
| Петров | Сергей | Олегович | |
| Локтев | Павел | Сергеевич |
Таблица 10 - Отношение R8, исходное для операции декартово произведение (таблица Проекты)
| R8 – перечень проектов |
| Проект |
| Автоматизация цеха 1 |
| Инновационные исследования |
Таблица 11 - Отношение R9, результат декартова произведения
| R9 – информация о сотрудниках | ||||
| Код сотрудника | Фамилия | Имя | Отчество | Проект |
| Иванов | Юрий | Игоревич | Автоматизация цеха 1 | |
| Орлов | Егор | Петрович | Автоматизация цеха 1 | |
| Юрков | Павел | Антонович | Автоматизация цеха 1 | |
| Степанов | Олег | Сергеевич | Автоматизация цеха 1 | |
| Петров | Сергей | Олегович | Автоматизация цеха 1 | |
| Локтев | Павел | Сергеевич | Автоматизация цеха 1 | |
| Иванов | Юрий | Игоревич | Инновационные исследования | |
| Орлов | Егор | Петрович | Инновационные исследования | |
| Юрков | Павел | Антонович | Инновационные исследования | |
| Степанов | Олег | Сергеевич | Инновационные исследования | |
| Петров | Сергей | Олегович | Инновационные исследования | |
| Локтев | Павел | Сергеевич | Инновационные исследования |
Если добавляется условие WHERE, то эта операция называется ограничением декартова произведения.
Комбинация декартова произведения и выборки может быть сведена к одной операции соединение.
5. Декомпозиция сложных операций
Операции реляционной алгебры могут быть очень сложными. Для упрощения такие операции можно разбить на ряд меньших операций реляционной алгебры и присвоить имена результатам промежуточных выражений. Для присваивания имен результатам операции реляционной алгеброй используется операция присваивания.
Операция переименования позволяет присвоить новое имя S выражению Е, а так же дополнительно переименовывать атрибуты.
Пример: Рассчитать премии сотрудникам 80% от оклада.
SELECT Сотрудники. Фамилия, Сотрудники. Имя, Сотрудники. Отчество, Сотрудники. Оклад*0,8 AS Премия
FROM Сотрудники;
Дата добавления: 2015-01-19; просмотров: 1614;
