Способы разбивочных работ

Разбивка сооружений является обратным по отношению к съемке действием и сводится к построению на местности характерных точек сооружения. Положение точек определяют теми же способами, которые применяют при выполнении съемочных работ. Однако при разбивке сооружений эти способы имеют отличие. Если в первом случае, то есть при съемках, эти способы применяют для непосредственных измерений, то при разбивках их используют при построениях на местности.

Выбор способа выполнения разбивочных работ определяют исходя из условий местности, типа сооружения, его размеров, требуемой точности. Главнейшими из этих способов и наиболее часто применяемыми являются способы полярных и прямоугольных координат, угловой и линейной засечек, створных засечек.

Способ полярных координат.Является одним из основных способов выноса в натуру точек главных и основных осей сооружения. Этот способ широко применяется при разбивке зданий, сооружений и конструкций с пунктов полигонометрических или теодолитных ходов при малом расстоянии от этих пунктов до выносимых в натуру точек. При этом способе положение точки сооружения на местности получают построением двух разбивочных элементов: заданного проектного угла β от стороны АВ разбивочной сети и расстояния d (рисунок 7.7). Значения полярного угла β и расстояния d получаем из решения обратной геодезической задачи по координатам пунктов геодезической разбивочной основы и проектной точки сооружения.

Для построения проектной точки С устанавливаем теодолит в точке А разбивочной сети. Затем наводим зрительную трубу теодолита на точку В и устанавливаем отсчет по лимбу 0^о00'. Вращаем алидаду до тех пор, пока отсчет по лимбу не станет равным проектному углу β, и по полученному направлению, задаваемому визирной осью трубы теодолита, откладываем мерным прибором проектное расстояние d. Точность построения проектной точки будет зависеть от точности построения теодолитом угла β и точности отложения проектного расстояния d. Таким образом, средняя квадратическая погрешность разбивки этим способом

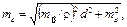
где m_β – погрешность построения проектного угла теодолитом;

m_d – погрешность построения линии мерным прибором;

ρ – переводной коэффициент из градусной меры в радианную.

Способ прямоугольных координат. Этот способ наиболее целесообразно использовать в том случае, когда на строительной площадке имеется строительная сетка. А если это городское строительство, – наличие закрепленных на местности красных линий застройки.

Разбивку проектной точки С выполняют по вычисленным значениям ее координат x и y от ближайшего пункта строительной сетки или красной линии (рисунок 7.8). Устанавливают теодолит в рабочее положение в точке А, визируют на точку В и в полученном створе откладывают проектное расстояние у. В полученной точке D устанавливают теодолит и строят прямой угол к направлению АВ. По перпендикуляру откладывают проектное расстояние х и закрепляют полученную точку. Для контроля положение точки С можно получить, выполнив разбивку от другого пункта разбивочной основы.

На погрешность положения проектной точки будут влиять погрешности m_x и m_y откладывания расстояний х и у, а также погрешность построения прямого угла m_β. Следовательно, точность построения точки этим способом определяется величиной средней квадратической погрешности

m_C = .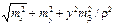

Cпособ прямой угловой засечки. Очень часто условия строительной площадки осложняют выполнение линейных измерений, и если при этом определяемая точка находится на значительном удалении от пунктов разбивочной основы, то целесообразно положение точки получать с помощью построения двух углов засечки β₁ и β₂ (рисунок 7.9).

Определяется положение искомой точки С при помощи двух вычисленных горизонтальных углов β₁ и β₂, получаемых при решении обратной геодезической задачи.

Проектное положение точки С находят, откладывая на исходных пунктах А и В углы β₁ и β₂. Точка С будет располагаться на пересечении двух створов АС и ВС.

Точность построения проектной точки С в способе прямой угловой засечки можно определить по формуле

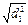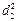где m_β – точность построения угла теодолитом;

γ – угол засечки;

d₁ и d₂ – расстояния от пунктов опорной сети до проектной точки.

Способ линейной засечки. Данный способ для выноса точек сооружения в натуру применяют в том случае, когда они расположены от пунктов строительной сетки или геодезической опорной сети на расстоянии, не превышающем длину мерного прибора. Искомая точка С на местности получается пересечением двух дуг, проведенных радиусами АС и ВС (рисунок 7.10). Наиболее удобно выполнять разбивку при помощи двух рулеток. От точки А по рулетке откладывают расстояние d₁, а от точки В по второй рулетке – расстояние d₂. Перемещая обе рулетки при нулях совмещенными с центрами пунктов А и В на пересечении концов отрезков d₁ и d₂, получаем положение определяемой точки.

На положение точки С окажут влияние погрешности откладывания расстояний d₁ и d₂. Точность положения точки на местности способом линейных засечек определяют по формуле

____

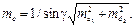
Способ створной засечки. Способ створной засечки очень часто применяют для выноса в натуру разбивочных осей зданий и сооружений, монтажных осей конструкций, технологического оборудования. Положение проектной точки С в способе створной засечки определятся пересечением двух створов, задаваемых между исходными точками (рисунок 7.11). Наилучшая засечка получается, когда створы пересекаются под прямым углом.

Створы желательно строить двумя теодолитами. В створном способе важное значение имеет центрировка теодолитов, особенно в направлениях, перпендикулярных к заданному створу.

Основными погрешностями при построении створов являются погрешности положения исходных точек, погрешности центрирования теодолита и визирных целей, погрешность визирования.

8 ГЕОДЕЗИЧЕСКИЕ РАБОТЫ