Установившийся режим автоколебаний

После включения АГ в нем начинается переходный процесс, в течение которого амплитуда автоколебаний возрастает от 0 до некоторого значения U_m. По окончании переходного процесса, длящегося t_пер, устройство переходит в режим установившихся автоколебаний (рис. 14.2). Время t_пер можно найти, составив и решив нелинейное дифференциальное уравнение, описывающее работу АГ.

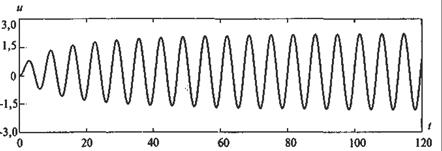
Рис. 14.2. Установление автоколебаний в АГ

В тех случаях, когда отсутствует необходимость определения t_пер, можно ограничиться исследованием только установившегося режима работы. Для такого анализа удобен метод гармонического баланса.

Ток электронного прибора i(t) в АГ может существенно отличаться от синусоидального вида и представлять собой периодическое колебание, состоящее из косинусоидальных или иной более сложной формы импульсов. Разложив периодическое колебание в ряд Фурье, выделим из него 1-ю гармонику сигнала, для которой запишем: I₁=I_mα₁, где 1_т - амплитуда импульса. Введем параметр - крутизну характеристики электронного прибора по 1-й гармонике сигнала:

S_y=I_l/U_y=I_ma_l/U_y,

где U_y - амплитуда напряжения на входе прибора, и запишем систему уравнений для комплексных амплитуд 1-й гармоники сигнала:

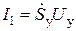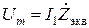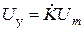; ; , (14.1)

где U_m - амплитуда гармонического напряжения на контуре (ранее было принято, что колебательная система фильтрует все гармоники, кроме 1-й); 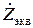- эквивалентное сопротивление контура на частоте 1-й гармоники сигнала; 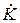- комплексный коэффициент обратной связи.

Совместное решение (14.1) дает основное уравнение АГ в комплексной форме по 1-й гармонике сигнала: 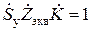. (14.2)

Это уравнение распадается на уравнения для произведения модулей и суммы фаз, соответственно называемые уравнениями баланса амплитуд и фаз: 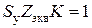; (14.3), 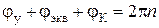. (14.4)

Уравнение баланса амплитуд (14.3) указывает на необходимость пополнения энергии в контур за счет цепи обратной связи, которое покрывало бы потери в нем, а уравнение баланса фаз (14.4) - на соблюдение условия фазировки: дополнительные колебания, вводимые в контур, должны совпадать по фазе с уже существующими. Количество дополнительной энергии можно регулировать за счет модуля коэффициента обратной связи К, а фазирование - за счет его фазы. Поскольку электронный прибор поворачивает фазу сигнала на величину, близкую к π, то согласно (14.4) на такую же величину должен происходить поворот фазы сигнала и за счет цепи обратной связи. Данному требованию отвечает трехточечная схема АГ (рис. 14.3).

Рис. 14.3. Трехточечная схема АГ

Первая из схем (рис. 14.3, а) называется емкостной, в ней модуль К=С₁/С₂, вторая (рис. 14.3, 6) - индуктивной, в ней модуль К=L₂/L₁.

Обе схемы могут рассматриваться как эквивалентные по отношению и к двухконтурной (рис. 14.3, в) и к иным схемам автогенератора.

С помощью уравнений (14.3) можно определить амплитуду автоколебаний в установившемся режиме, для чего представим систему (14.1) в виде двух уравнений: 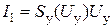; 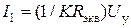. (14.5)

Их совместное решение позволяет найти амплитуды тока 1₁ и напряжения: U_m=I₁R_m в установившемся режиме. Графическое решение уравнений приведено на рис 14.4. Для существования устойчивого режима автоколебаний необходима одна точка А пересечения графиков. Согласно общей теории устойчивости стационарный режим АГ является устойчивым, если малые отклонения амплитуды относительно установившегося значения возвращают систему в первоначальное состояние.

Рис. 14.4. Графическое решение уравнений.

Пусть колебания синусоидальны и определяются выражением: u(t)=U_yстe^α(U)tcosωt. Тогда согласно сформулированному условию устойчивости следует иметь α(U)=0 при U=U_уст, α(U)<0 при U>U_уст, α(U)>0 при U<U_уст, что эквивалентно следующему неравенству:

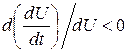. (14.6)

При выполнении (14.6) любое увеличение или уменьшение амплитуды U относительно U_уст возвращает систему в первоначальное состояние, что свидетельствует об устойчивости стационарного режима автоколебаний. Полная электрическая схема однотактного транзисторного АГ с цепью питания и смещения приведена на рис. 14.5, а, двухтактного - на рис. 14.5, б.

Рис. 14.5. Схемы транзисторного АГ