Теоретические сведения. Поле излучения плоской площадки

Поле излучения плоской площадки. Пусть имеется плоская площадка 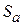любой формы (рис. 4.3), в каждой точке которой заданы векторы электрического и магнитного полей:

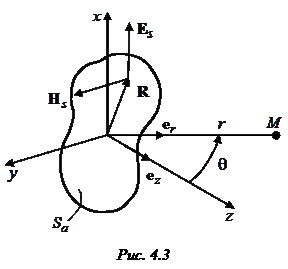
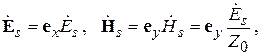
где 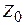– волновое сопротивление среды, а 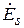, вообще говоря, является функцией точки 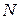на поверхности площадки ( 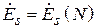). В теории излучения показано, что такая площадка создает в пространстве электромагнитное поле. В даль­ней зоне это поле (поле излучения) пред­ставляется в виде

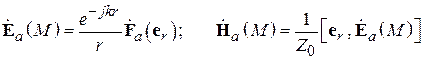, (4.1)

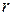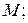
где – расстояние от центра площадки до точки наблюдения – орт, направленный из точки на точку 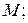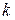– волновое число.

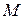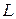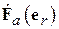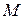Точка находится в дальней зоне, если удовлетворяются 3 неравенства: , где – наибольший линейный размер системы (излучающей площадки). Как видно из (4.1), поле в дальней зоне представляется в виде произведения двух функций – скалярной , зависящей только от расстояния , и векторной , зависящей от направления из на точку наблюдения . Эта функция называется характеристикой 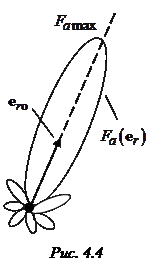направленности излучающей площадки. Как и всякий вектор, ее можно представить в виде , где орт 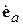указывает пространственную ориентацию (поляризацию) вектора 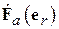. Согласно (4.1), она совпадает с поляризацией вектора 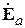. Скалярная характеристика направленности 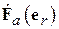, которая несет информацию об амплитудном распределении поля излучения в зависимости от , может быть записана в виде произведения , где 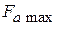– значение характеристики направленности в направлении максимального излучения (орт на рис. 4.4). 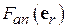Функция называется нормированной характеристикой направленности. Очевидно,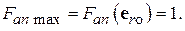

Характеристику направленности площадки можно рассчитать, если известно распределение поля 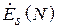по ее поверхности 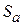. В случае синфазного распределения поля ( 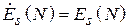) соответствующая формула выглядит так:

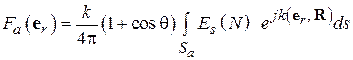, (4.2)

где вектор 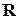и угол 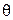показаны на рис. 4.1. В данном случае направление максимального излучения нормально к 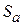, т. е. 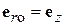, = 0, а из (4.2) следует, что

.

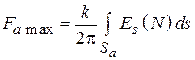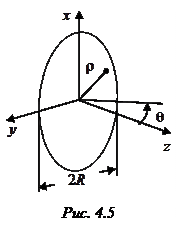Круглая площадка с центрально-симметрич­ным распределением поля.Допустим, что площадка имеет форму круга (рис. 4.5), а распределение поля центрально-симметричное, т. е. 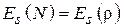. В таком случае и характеристика направленности осесимметрична, т. е. является функцией одного угла 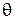. После соответствующих преобразований интеграла (4.2) выражение для характеристики направленности такого раскрыва можно привести к следующему виду:

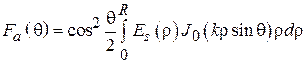, (4.3)

где 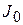– функция Бесселя нулевого порядка.

Если распределение поля однородно, т. е. 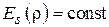, то, используя (4.2) и (4.3), получим нормированную характеристику на­правленности в виде

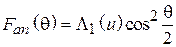, (4.4)

где 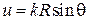, 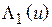– лямбда-функция 1-го порядка [6]. При малых значениях угла 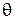и боль­ших значениях параметра kR можно считать, что 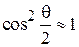и зависимость 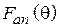при малых углах определяется в основном первым множителем в (4.4). Вид функции 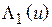показан на рис. 4.6. Как видно, это осциллирующая функция, имеющая главный и ряд боковых лепестков. Ширина главного лепестка по уровню 0,707

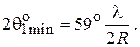(4.5)

Формула (4.5) выражает фундаментальный факт: ширина главного лепестка определяется отношением радиуса площадки к длине волны. Чем больше отношение 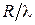, тем уже лепесток, тем более остронаправленным является излучение. Заметим, что ширина диаграммы (4.5), полученная для однородного распределения поля, является минимально возможной при данном отношении 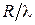; именно поэтому в (4.5) фигурирует индекс 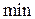. В то же время при однородном распределении поля получается максимальный уровень первого бокового лепестка (0,132 или –17,6 дБ).

Если распределение поля по апертуре неоднородно ( ), то для расчета характеристики направленности его удобно аппроксимировать полиномом вида

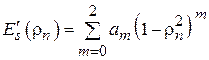, (4.6)

где 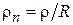– нормированный радиус.

Приравнивая значения этого полинома и реального распределения в точках 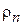= 0; 0,5; 1,0 , для коэффициентов 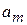получим систему уравнений 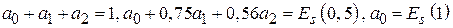, решение которой дает следующие выражения для коэффициентов:

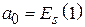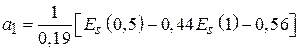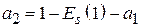, , . (4.7)

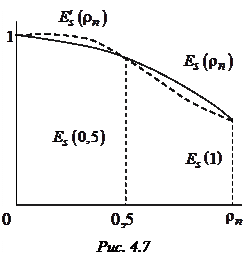При практических расчетах после нахождения коэффициентов по (4.7) целесообразно рассчитать значения полинома и построить соответствующий график 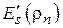совместно с графиком истинного распределения 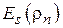. Это даст возможность судить о качестве аппроксимации (рис. 4.7).

Примечание: Для повышения точности аппроксимации поля в ракрыве ЗА целесообразно записать систему уравнений более высокого порядка чем три (порядок равен выбранному числу узлов аппроксимации), затем решить ее численно и найти поле в раскрыве по формуле (4.6) с соответствующим числом членов суммы.

Подставляя аппроксимирующий полином (4.6) в формулу (4.3), получим нормированную характеристику направленности

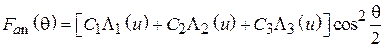, (4.8)

где коэффициенты 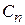равны:

.

В (4.8) входят лямбда-функции -го порядка 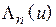. Значения этих функций можно вычислить по формул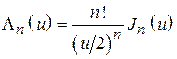е , где 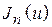– функция Бесселя n-го порядка [6] .

По рассчитанной характеристике направленности 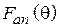можно найти ширину ее главного лепестка 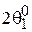, которая окажется больше минимально возможной, найденной по формуле (4.5). Отношение 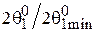называется коэффициентом расширения луча (КРЛ). Эта величина показывает, во сколько раз ширина основного лепестка (луча) при данном распределении больше, чем при однородном распределении, но при том же значении 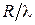. Обычно КРЛ равен 1,1…1,3.

По рассчитанной характеристике 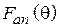можно также найти уровень первого бокового лепестка (УБЛ). При распределении поля, спадающем от центра к краю апертуры, УБЛ оказывается меньше, нежели при однородном распределении (0,132). При этом, чем быстрее спадает поле, тем меньше УБЛ.

Коэффициент направленного действия и апертурный КИП площадки. Важнейшим параметром, характеризующим направленность любой антенны, является коэффициент направленного действия (КНД). По одному из нескольких эквивалентных определений КНД есть отношение плотности потока мощности на единицу телесного угла в направлении максимального излучения к средней по полному телесному углу 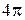плотности потока мощности той же антенны.

Свяжем это определение с характеристикой направленности. Известно, что величина 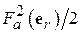есть плотность потока мощности на единицу телесного угла в направлении орта . Следовательно, в направлении максимального излучения она равна 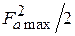. Чтобы получить среднюю по телесному углу 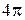плотность потока мощности, нужно полную мощность 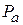, излучаемую площадкой, разделить на 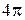. Тогда, в соответствии с определением, КНД площадки

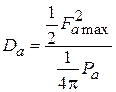. (4.9)

Величина, стоящая в числителе (4.9):

.

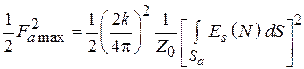Значение мощности 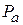, входящее в знаменатель (4.9), можно найти через 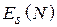как поток вектора Пойнтинга через площадку :

.

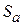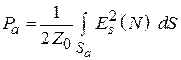Тогда выражение (4.9) для КНД приводится к виду

, (4.10)

где

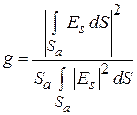. (4.11)

Как видно из (4.10), основным фактором, определяющим КНД синфазной апертуры, является отношение ее геометрической площади 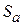к квадрату длины волны. С ростом этого отношения растет и КНД, что вполне согласуется с полученным ранее выводом о возрастании направленности излучения с ростом .

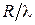Коэффициент 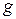, входящий множителем в (4.10), учитывает влияние на КНД формы распределения поля по площадке. Он называется апертурным коэффициентом использования площади (апертурный КИП). Из формулы (4.11) видно, что максимально возможное значение 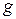, равное 1, получается при равномерном распределении. При неравномерном распределении 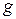< 1. Обычно 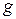= 0,6...0,9. Поскольку апертурный КИП зависит только от распределения поля , его можно вычислить, зная коэффициенты аппроксимирующего полинома (4.6):

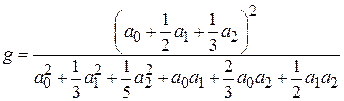. (4.12)

Распределение поля в апертуре параболического зеркала. Если диаграмма направленности облучателя 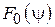осесимметрична, т. е. зависит только от угла 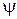, то поле в апертуре будет центрально-симметричным: 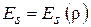. Функция 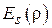зависит от диаграммы облучателя 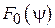. Связь между этими двумя функциями можно установить с помощью условия энергетического баланса (рис. 4.2) в лучевых трубках до и после отражения от зеркала. Очевидно, в конической трубке с телесным углом заключена та же мощность, что и в цилиндрической трубке с площадью 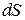(см. рис. 4.2). Расчет показывает, что распределение поля в функции нормированного радиуса 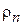выражается через ДН облучателя следующим образом:

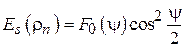. (4.13)

Постоянный множитель в (4.13) опущен, а нормированный радиус 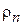и угол 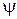связаны при этом жестким соотношением

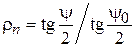. (4.14)

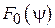Расчет по известной ДН выполняется так. Задают последовательностью углов 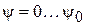. Для каждого из них, зная 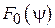, находят по (4.14) значения 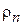, а по (4.13) – соответствующие значения . По найденной функции можно рассчитать нормированную характеристику направленности апертуры зеркала. Для этого нужно найти коэффициенты аппроксимирующего полинома и проверить качество аппроксимации. Далее рассчитываются коэффициенты 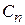и нормированная ДН по формуле (4.8). Располагая этой ДН, можно найти ширину главного лепестка 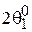и КРЛ. Наконец, находятся апертурный КИП 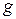и КНД.

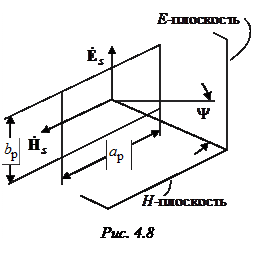Облучатели зеркальных антенн.

Одним из наиболее распространенных облучателей зеркальных антенн являются рупора с прямоугольным раскрывом, возбуждаемые прямоугольным волноводом (рис. 4.8). При их использовании возникает вопрос об осевой симметрии их диаграммы направленности, которая необходима для создания в апертуре зеркала осесимметричного распределения поля. Повлиять на ДН рупора можно только одним способом – выбором размеров апертуры 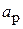и 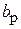. Однако можно убедиться, что ни одна из комбинаций этих размеров не приводит к полностью осесимметричной ДН. Это видно хотя бы из того, что в плоскостях 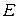и 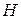ДН рупора описываются разными функциями угла 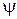. В Е-плоскости это выражение имеет вид

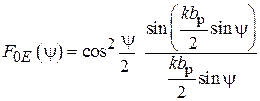, (4.15)

а в H-плоскости, соответственно,

. (4.16)

Поэтому возможно создание лишь приближенно осесимметричной ДН. Потребуем, чтобы значения ДН в обеих плоскостях совпали при 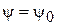. Тогда процедура расчета размеров рупора может быть следующей. Известны угол 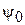и уровень облучения края зеркала . Из (4.15) и (4.16) вытекают тогда следующие равенства:

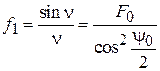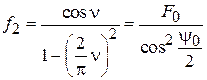, , (4.17)

где 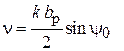для функции f1и 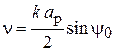для функции f2. Разрешить равенства (4.17) относительно n можно, имея графики функций, стоящих в равенствах слева. Эти графики приведены на рис. 4.9. Зная n, а также 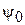и 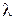, легко найт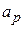и и .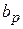

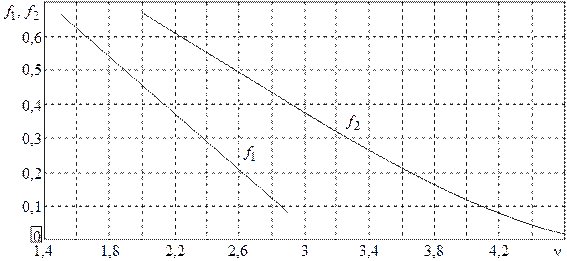
Рис. 4.9

Если размеры рупора выбраны из условия 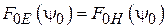, то диаграмму направленности 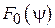можно далее считать приближенно осесимметричной, а для ее аналитического представления использовать одну из формул (4.15) или (4.16). В дальнейшем остановимся на (4.15).

Переливание мощности через край зеркала. Эффективность облучателя. В зеркальных антеннах с облучателями традиционных типов (рупор, полуволновый вибратор с рефлектором и т. п.) не вся мощность облучателя перехватывается зеркалом. Действительно, доля мощности , соответствующая той части ДН облучателя, которая выходит за пределы угла 2y0на рис. 4.6, переливается через край зеркала и не попадает в его апертуру. Это обстоятельство снижает КНД антенны в целом, который получается меньше КНД апертуры 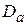. По определению, КНД антенны представляется отношением типа (4.9)

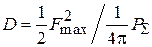, (4.18)

где 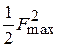– плотность потока мощности антенны на единицу телесного угла в направлении ее максимального излучения. Строго говоря, в этом направлении складывается 2 поля – поле излучения апертуры и поле заднего излучения облучателя (рис. 4.10). Однако последнее обычно незначительно и им можно пренебречь. Следовательно, в (4.18) можно сделать замену 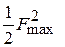на 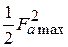. Деля и умножая (4.18) на 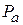, получим

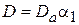, (4.19)

где 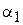– отношение мощности, падающей на зеркало и проходящей затем апертуру ( 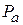), к полной мощности облучателя ( 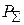). Это отношение и учитывает факт переливания мощности за край зеркала и называется эффективностью облучателя. Эффективность облучателя можно рассчитать по известной ДН облучателя и углу облучения края зеркала:

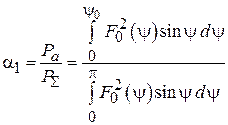. (4.20)

Подставляя (4.10) в (4.19), получим

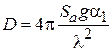. (4.21)