Исследование зависимости угла смачивания от скорости для воды в кварцевой щели и при капиллярном поднятии в стеклянных цилиндрических капиллярах.
В Средние века не существовало понятия специального «детского костюма», малыши во многом одевались точно также как папа или мама. Цветом пелёнок у бедняков чаще всего выступал коричнево-бежевый, то есть цвет неокрашенного полотна, более состоятельные люди предпочитали зелёный (цвет юности), или же красный. Детство по средневековым понятиям заканчивалось в 7 лет, и бывший ребёнок становился «отроком» (лат. puer); порой к этому времени его женили или выдавали замуж, причём если речь шла о девочке из знатного рода, ей предстояло воспитываться в семье мужа. «Отрок» от 7 и до 14 лет одевался уже по взрослой моде, за единственным исключением — не покрывал голову. В 14 лет подросток считался совершеннолетним, крестьянский мальчик или девочка работали в поле, отпрыски знатных родов порой командовали войсками или управляли частью отцовского владения. В это время и вплоть до старости им предписывалось одеваться в соответствии с веяниями моды, выбирая тот или иной элемент костюма, руководствуясь требованиями ситуации, а также собственным вкусом.
Исследование зависимости угла смачивания от скорости для воды в кварцевой щели и при капиллярном поднятии в стеклянных цилиндрических капиллярах.
Поскольку изучение зависимости угла смачивания от скорости имеет не только теоретическое (важное для понимания закономерностей смачивания), но и большое практическое значение (в различных природных и технологических процессах важно знать динамику смачивания), а данных по зависимости углов смачивания от скорости для воды и водных растворов на поверхности полярных твёрдых тел в литературе практически не было, нами были проведены соответствующие опыты [212,213].
Была изучена зависимость угла смачивания от скорости для воды в кварцевой плоскопараллельной щели, составленной из двух плоскопараллельных полированных пластин из природного кристаллического кварца размером 40x40 мм [212]. Ширина
щели составляла 400 мкм. Методика эксперимента описана в приложении.
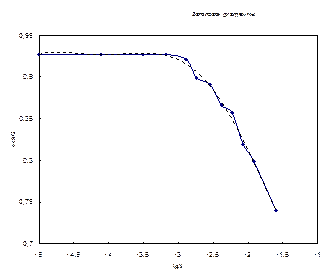 Результаты опытов по радиальному растеканию воды в кварцевой щели позволили получить зависимость угла смачивания от скорости, которая приведена на рис.13.
Результаты опытов по радиальному растеканию воды в кварцевой щели позволили получить зависимость угла смачивания от скорости, которая приведена на рис.13.
Рис.13. Зависимость угла смачивания ( 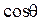 )от скорости
)от скорости 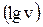 , измеренная при растекании воды в плоскопараллельной кварцевой щели.
, измеренная при растекании воды в плоскопараллельной кварцевой щели.
Как видно из рис.13, на зависимости 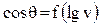 хорошо видна область независимости θ от скорости, а также прямолинейная зависимость
хорошо видна область независимости θ от скорости, а также прямолинейная зависимость 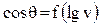 для скоростей, больших 1,3·10-3 см/с, что согласуется с уравнением (Ш-69 ) теории Блейка и Хэйнса.
для скоростей, больших 1,3·10-3 см/с, что согласуется с уравнением (Ш-69 ) теории Блейка и Хэйнса.
Были также проведены опыты по капиллярному поднятию воды и водных растворов электролитов в цилиндрических стеклянных капиллярах из термометрического стекла (завод термометрического стекла в г.Клин) с радиусом просвета 52 и 54 мкм. Для исследования капиллярного поднятия нами использовались как свежетянутые капилляры (капилляры заводского изготовления, не бившие в контакте с водой после вытягивания), так и капилляры, подвергнутые стандартной процедуре очистки (см. методику в приложении). Как уже упоминалось, высокотемпературная обработка силикатов приводит к значительному дегидроксилированию поверхности [77]. Поэтому капилляры, полученные вытягиванием из расплава (~1000°) имеют дегидроксилированную поверхность. В контакте с парами воды гидроксильный покров восстанавливается частично. Полное восстановление гидроксильного покрова, по данным [77], происходит только при контакте с водой. Таким образом, поверхность свежетянутых капилляров, находящихся в равновесии с парами воды, является частично дегидроксилированной. Процедура очистки исходных капилляров, связанная с обработкой азотной кислотой и длительным промыванием водой, полностью восстанавливает 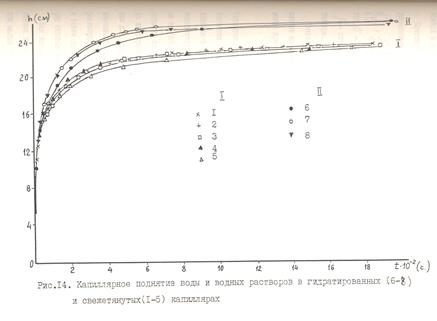 гидроксильный покров поверхности. Поэтому капилляры, прошедшие процедуру очистки, будем в дальнейшем называть гидроксилированными. Кривые кинетики капиллярного поднятия в свежетянутых и гидратированных капиллярах, полученные для воды и различных растворов электролитов (кривые усреднены по 5-10 опытам) приведены на рис.14. В отличие от свежетянутых капилляров, где конечная высота капиллярного поднятия не устанавливалась в течение нескольких суток, в гидратированных капиллярах величина равновесного поднятия hm устанавливалась через несколько часов после начала опыта и затем практически не изменялась. Кроме того, высота конечного поднятия в гидратированных капиллярах оказалась на 1–1,5 см больше, чем в свежетянутых.
гидроксильный покров поверхности. Поэтому капилляры, прошедшие процедуру очистки, будем в дальнейшем называть гидроксилированными. Кривые кинетики капиллярного поднятия в свежетянутых и гидратированных капиллярах, полученные для воды и различных растворов электролитов (кривые усреднены по 5-10 опытам) приведены на рис.14. В отличие от свежетянутых капилляров, где конечная высота капиллярного поднятия не устанавливалась в течение нескольких суток, в гидратированных капиллярах величина равновесного поднятия hm устанавливалась через несколько часов после начала опыта и затем практически не изменялась. Кроме того, высота конечного поднятия в гидратированных капиллярах оказалась на 1–1,5 см больше, чем в свежетянутых.
Как известно, высота капиллярного поднятия h в цилиндрическом капилляре определяется уравнением
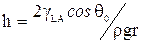 ,
,
где ρ – плотность воды, g – ускорение силы тяжести, r – радиус капилляра.
В соответствии с уравнением (Ш-70), различие высот поднятия в свежетянутых и гидратированных капиллярах может быть связано только с различием в величинах угла смачивания, поскольку все остальные величины, определяющие высоту поднятия в капилляре, одинаковы.
Аналогичная разница капиллярного поднятия для свежетянутых и гидратированных капилляров была обнаружена впоследствии в опытах на кварцевых капиллярах Березкиным и др. [214].
Наблюдаемое постепенное возрастание капиллярного поднятия в
свежетянутых капиллярах связано, по-видимому, с медленным
гидроксилированием их поверхности (образование в контакте с водой силанольных групп ). Угол смачивания при этом уменьшается и высота поднятия растет. Кинетика капиллярного поднятия наиболее полно описывается уравнением Бриттина [216]:
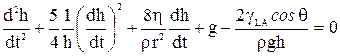 ,
,
где g– поверхностное натяжение жидкости , η – ее вязкость; ρ – плотность; g – ускорение силы тяжести; r – радиус капилляра.
Поскольку первые два члена этого уравнения по порядку величины намного меньше остальных, то ими для данного случая можно пренебречь, и тогда уравнение (Ш-71) упрощается
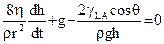 (III-72)
(III-72)
Согласно этому уравнению, зная изменение скорости капиллярного поднятия 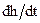 можно проследить за изменением угла смачивания в процессе поднятия. Рассчитанные таким образом кривые зависимости cosθ от скорости капиллярного поднятия изображена на рис. 15 в координатах
можно проследить за изменением угла смачивания в процессе поднятия. Рассчитанные таким образом кривые зависимости cosθ от скорости капиллярного поднятия изображена на рис. 15 в координатах 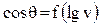 . Скорости капиллярного поднятия
. Скорости капиллярного поднятия 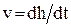 определялись методом численного дифференцирования кривых
определялись методом численного дифференцирования кривых 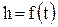 . На рис. 15 приведен ряд кривых для гидратированных капилляров, характеризующих интервал изменений поднятия для изученной серии капилляров и разных растворов, кривая для поднятия воды в свежетянутых капиллярах, а также приведена для сравнения
. На рис. 15 приведен ряд кривых для гидратированных капилляров, характеризующих интервал изменений поднятия для изученной серии капилляров и разных растворов, кривая для поднятия воды в свежетянутых капиллярах, а также приведена для сравнения 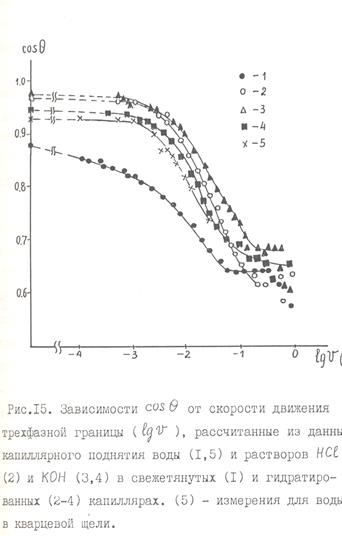 зависимость
зависимость 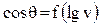 для опытов по растеканию воды в кварцевой щели.
для опытов по растеканию воды в кварцевой щели.
Как видно из рис.15, все представленные кривые для гидратированных поверхностей стекла и кварца имеют аналогичный вид: при малых скоростях (<10-3см/с ) угол смачивания практически не изменяется при увеличении скорости, в интервале скоростей 10-3 –
10-1 см/с наблюдается прямолинейная зависимость в координатах 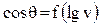 и затем при скоростях > 10-1 см/с, несмотря на большой разброс экспериментальных данных, можно, по-видимому, выделить вторую область независимости угла смачивания от скорости.
и затем при скоростях > 10-1 см/с, несмотря на большой разброс экспериментальных данных, можно, по-видимому, выделить вторую область независимости угла смачивания от скорости.
Полученные результаты качественно согласуются с результатами работ [26,30]. Зависимость 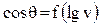 , полученная на свежетянутых капиллярах, отличается от остальных отсутствием плато при малых скоростях поднятия, где наблюдается медленное постоянное уменьшение угла смачивания (возрастание
, полученная на свежетянутых капиллярах, отличается от остальных отсутствием плато при малых скоростях поднятия, где наблюдается медленное постоянное уменьшение угла смачивания (возрастание 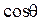 ).
).
Медленное уменьшение краевого угла, как уже указывалось, связано с регидроксилированием поверхности свежетянутых капилляров.
Интересно сопоставить полученные нами данные с результатами других авторов по зависимости углов смачивания от скорости движения ТФГ для воды и гидрофобных и гидрофобизированных поверхностях.
Из таблицы 1 видно, что величина максимального изменения 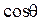 при увеличении скорости (
при увеличении скорости ( 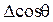 ) для гидрофильных поверхностей значительно выше, чем для гидрофобных, что связано, по-видимому, с сильным ориентирующим действием полярных твердых тел на молекулы воды. По-видимому, поэтому и максимальная скорость Vmax после которой начинается вторая область независимости
) для гидрофильных поверхностей значительно выше, чем для гидрофобных, что связано, по-видимому, с сильным ориентирующим действием полярных твердых тел на молекулы воды. По-видимому, поэтому и максимальная скорость Vmax после которой начинается вторая область независимости 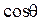 от скорости, для гидрофильных тел также значительно выше.
от скорости, для гидрофильных тел также значительно выше.
По полученным зависимостям 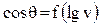 можно определить константы теории Блейка и Хэйнса Δn и K, поскольку эти зависимости линейны в области скоростей 10-3 – 10-1 см/с. По тангенсу угла наклона экспериментальной прямой
можно определить константы теории Блейка и Хэйнса Δn и K, поскольку эти зависимости линейны в области скоростей 10-3 – 10-1 см/с. По тангенсу угла наклона экспериментальной прямой 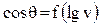 и отрезку, отсекаемому ею на оси абсцисс, были определены величины Δn, K и λ, (в первом приближении l
и отрезку, отсекаемому ею на оси абсцисс, были определены величины Δn, K и λ, (в первом приближении l 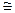 (Dn)-1/2). Для зависимости полученной для свежетянутых капилляров, расчет проводился по
(Dn)-1/2). Для зависимости полученной для свежетянутых капилляров, расчет проводился по
Таблица I
Сравнение данных по зависимости угла смачивания от скорости, полученных разными авторами на различных системах
| Система | 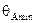 ,
град. ,
град.
| 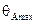 , град. , град.
| 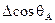
| 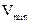 ,
см/с ,
см/с
| 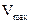 ,
см/с ,
см/с
| Ссылки |
| Кварцевая щель-вода | - | - | 8 10-4 | - | наши данные | |
| Стекло – 10-3N КОН (гидратир. капилляр) | 0,30 | 5·10-4 | 1·10 -1 | то же | ||
| Стекло– 10-3 N HCl (гидратир.капилляр) | 0,35 | З·10-4 | 1,6 10-1 | - | ||
| Стекло - вода (свежетянутый капилляр) | 0,24 | - | 5·10-2 | - | ||
| Стекло, покрытое (СH3)3SiCl – вода | 0,17 | 8·10-4 – 4,2·10-3 | 5·10-3 | [216] | ||
| Стекло, покрытое (СH3)2SiCl2 – вода | 0,16 | 8.10-4. 4,2·10-3 | 1 10-2 | [216] | ||
| Стекло, покрытое (C2H5)3SiCl– вода | 78,5 | 0,03 | 8·10-4 – 4,2·10-3 | 1 10-2 | [216] | |
| Стекло, покрытое (C2H5)2SiCl2 – вода | 0,06 | 8·10-4 – 4,2·10-3 | 1 10-2 | [216] | ||
| Полиэтилен – вода | 0,16 | 1,7·10-3 | 2,9·10-2 | [30] | ||
| Парафин – вода | 0,15 | - | 4 10-2 | [26] | ||
| Политетрафторэтилен-вода | 0,09 | 1 10-3 | 1,2 10-2 | [217] |
двум линейным участкам кривой 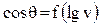 , имеющим разный наклон, соответствующий медленному и быстрому падению
, имеющим разный наклон, соответствующий медленному и быстрому падению 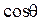 с увеличением скорости. Рассчитанные таким образом константы уравнения Блейка-Хэйнса приведены в таблице 2.
с увеличением скорости. Рассчитанные таким образом константы уравнения Блейка-Хэйнса приведены в таблице 2.
Таблица 2
Константы уравнения Блейка-Хэйнса, вычисленные по экспериментальным данным
| Система | cosθ0 | Δn·10-18, м-2 | Λ, нм | K·10-3, с-1 | |
| Стекло– 10-2N HCl (гидратир. капилляр) | 0,976 | 1,7 | 0,8 | ||
| Стекло – 10-2N КОН (гидратир. капилляр) | 0,976 | 1,3 | 0,9 | ||
| Кварц-вода (щель) | 0,927 | 1,4 | 0,9 | ||
| Стекло-вода (свежетяну-тый капилляр | Крутой наклон | 0,881 | 1,01 | 1,0 | 7,9 |
| Пологий наклон | 0,881 | 0,44 | 1,5 | 0,25 |
Из таблицы 2 видно, что все вычисленные значения констант как для кварца, так и для гидратированного стекла хорошо сходятся между собой. Значения константы Δn , представляющей собой по Блейку и Хэйнсу концентрацию активных центров на поверхности стекла и кварца, оказались лежащими в пределах 1-2·1018 м-2. Эти величины находятся в согласии с литературными данными, по которым величина поверхностной концентрации ОН-групп предельно гидроксилированной поверхности пористых стекол, силикагелей и аэросилов составляет 4,2-5,7·1018 м-2. Тер-Минасян-Сарага [218] при исследовании адсорбции бромида додецилтриметиламмония на поверхности полированных пластин из стекла и плавленого кремнезема получила для концентрации поверхностных силанольных групп значения 1,9·1018 и 1,5·1018 м-2 на стекле и кварце соответственно. Как видно из таблицы , величины Δn, полученные нами для отекла и кварца, хорошо согласуются с результатами этой работы. Сравнение значений Δn, рассчитанных по крутому и пологому участкам наклона кривой 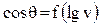 для свежетянутых капилляров, показывает, что рассчитанная по крутому участку (большие скорости поднятия) величина Δn в 2-3 раза превышает величину Δn, рассчитанную по пологому участку (при малых скоростях поднятия). Последняя, по-видимому, и отражает слабую степень гидроксилирования поверхности свежетянутых капилляров. Как известно, регидроксилирование поверхности кремнеземов в воде связано со значительной энергией активации [77], причем повышение температуры позволяет ускорить этот процесс и полностью восстановить гидроксильный покров. По-видимому, при больших скоростях движения ТФГ выделение теплоты гидроксилирования и теплоты смачивания приводит к локальному повышению температуры зоны ТФГ, что способствует быстрому прохождению процесса регидроксилирования и понижению угла смачивания. Поэтому значение Δn, рассчитанное для больших скоростей поднятия в свежетянутых капиллярах практически совпадает со значением Δn для гидратированного стекла и кварца.
для свежетянутых капилляров, показывает, что рассчитанная по крутому участку (большие скорости поднятия) величина Δn в 2-3 раза превышает величину Δn, рассчитанную по пологому участку (при малых скоростях поднятия). Последняя, по-видимому, и отражает слабую степень гидроксилирования поверхности свежетянутых капилляров. Как известно, регидроксилирование поверхности кремнеземов в воде связано со значительной энергией активации [77], причем повышение температуры позволяет ускорить этот процесс и полностью восстановить гидроксильный покров. По-видимому, при больших скоростях движения ТФГ выделение теплоты гидроксилирования и теплоты смачивания приводит к локальному повышению температуры зоны ТФГ, что способствует быстрому прохождению процесса регидроксилирования и понижению угла смачивания. Поэтому значение Δn, рассчитанное для больших скоростей поднятия в свежетянутых капиллярах практически совпадает со значением Δn для гидратированного стекла и кварца.
Вычисленные нами константы Δn, K и λ были подставлены в полное уравнение Блейка-Хэйнса (III-67) [209]. Рассчитанные по этому уравнению теоретические кривые зависимости соs θ = f(lg v) приведены в виде сплошных линий на рис. 15. Из сравнения теоретических кривых с экспериментальными точками видно, что для всех рассмотренных случаев наблюдается хорошее совпадение эксперимента и теории, расхождение наблюдается лишь в области больших скоростей, где, по-видимому, для описания процесса растекания недостаточно рассмотрения только молекулярного переноса в зоне ТФГ и, по-видимому, нужно привлекать гидродинамическое рассмотрение растекания исследуемой системы.
Совпадение вида зависимостей соs θ = f(lg v),полученной в прямом эксперимента по смачиванию (кварцевая щель) и рассчитанной по капиллярному поднятию, говорит о том, что с учетом кинетики изменения угла смачивания при изменении скорости уравнение Бриттина правильно описывает процесс капиллярного поднятия для изученных систем. Нет нужды также подчеркивать, что угол смачивания не является постоянным при капиллярном поднятии и зависимость соs θ = f(lg v) необходимо включать в уравнение процесса капиллярного движения жидкости. К сожалению, эта зависимость до сих пор часто не учитывается при рассмотрении капиллярного поднятия жидкостей [198].
Влияние температуры на зависимость угла смачивания от скорости для дегидратированной поверхности стекла (свежетянутые капилляры)
Для дальнейшего выяснения закономерностей кинетики смачивания была проведена серия опытов по температурной зависимости угла смачивания от скорости, а также по влиянию условий предварительной обработки поверхности твердого тела на этот процесс.
Была исследована кинетика капиллярного поднятия воды в капиллярах, аналогичных изученным ранее, при температурах от 20 до 70°C. Изучались свежетянутые капилляры с различной предварительной подготовкой поверхности. Все эти опыты проводились в атмосфере насыщенных паров воды (методика дана в приложении), но время предварительного контакта с парами было разное.
Со свежетянутыми капиллярами было проведено две серии опытов. Первая – с капиллярами, которые непосредственно перед опытом приводились в термическое равновесие и в равновесие с насыщенными парами воды, вторая — с капиллярами, которые были приведены в термическое равновесие, но, по-видимому, адсорбционная пленка воды на их поверхности не была равновесна. Капилляры первой серии выдерживали в парах не менее 6 часов, капилляры второй серии — 1-1,5 часа. Первые условно будем называть "равновесными", вторые — "неравновесные". Время достижения равновесия (6 ч.) было определено по результатам предварительных опытов с разным временем выдерживания капилляров в парах.
Для получения более достоверных результатов капиллярное поднятие при каждой температуре проводилось в 4-6 капиллярах. Во всех случаях наблюдалась очень хорошая сходимость кривых h-t на разных капиллярах.
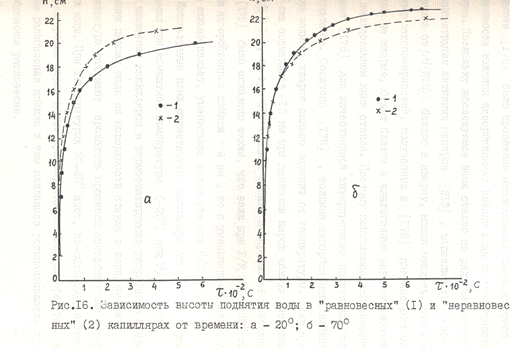
При сравнении кривых капиллярного поднятия в "равновесных" и "неравновесных" капиллярах при одной температуре была обнаружена интересная закономерность. Для 20°C кривые h-t для "равновесных" капилляров шли заметно ниже кривых h-t для "неравновесных" (рис. 16а). С повышением температуры эта разница постепенно уменьшалась и практически исчезла при 50 и 60°C. При 70°C наблюдалось обратное явление: кривые h-t для "равновесных" капилляров были несколько выше, чем для "неравновесных" (рис. 16б). Обнаруженная закономерность связана, по-видимому, с кинетикой образования равновесной адсорбционной пленки воды на поверхности стекла при разных температурах. В работе [175] было проведено исследование температурной зависимости толщины адсорбционных пленок воды на поверхности кварца. Поскольку исследуемое нами стекло по ряду параметров (концентрация активных центров [213], зависимость ζ-потенциала от pH [219]) близко к кварцу, можно ожидать, что характер закономерностей, полученных в [175] для адсорбционных пленок на кварце, будет близок к аналогичным закономерностям на исследованном нами стекле. Поэтому попытаемся использовать данные [175] для качественной интерпретации полученных нами результатов. Согласно [175], толщина адсорбционных пленок паров воды на кварце сильно зависит от температуры. Если при 10°C она составляет ~10 нм при давлении паров вблизи насыщения (Р/Рs 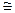 1), то при 67°C толщина плёнки не превышает монослоя. В [175] было показано также, что если при Р/Р5
1), то при 67°C толщина плёнки не превышает монослоя. В [175] было показано также, что если при Р/Р5 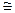 1 и 27°C толщина адсорбционной плёнки ~4 нм, то с уменьшением давления она сильно падает, уменьшаясь вдвое уже при Р/Рs
1 и 27°C толщина адсорбционной плёнки ~4 нм, то с уменьшением давления она сильно падает, уменьшаясь вдвое уже при Р/Рs 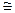 0,97.
0,97.
Используемые нами свежетянутые капилляры находились в равновесии при комнатной температуре (~20°C) при Р/Рs < 0,55. При помещении капилляров в термостатирующее устройство с насыщенными парами воды на поверхности стекла в зависимости от температуры начинают проходить процессы адсорбции или десорбции воды. При температурах 20-40°C идет, по-видимому, активная адсорбция паров воды. Причем, чем меньше температура, тем толще равновесная пленка и тем медленнее устанавливается адсорбционное равновесие.
Поэтому и наблюдается такая разница для кривых h-t для "равновесных" и "неравновесных" капилляров. При температурах 50 и 60°C толщина адсорбционной пленки воды меньше и разницы в поведении "равновесных" и "неравновесных" капилляров нет, потому что адсорбционное равновесие в этом случае достигается, по-видимому, за 1-1,5 ч. При 70°C толщина равновесной адсорбционной пленки настолько мала, что при помещении капилляра в термостат происходит процесс десорбции воды с поверхности и для "равновесных" капилляров толщина пленки меньше, чем для "неравновесных". Поэтому и кривые h-t меняют положение.
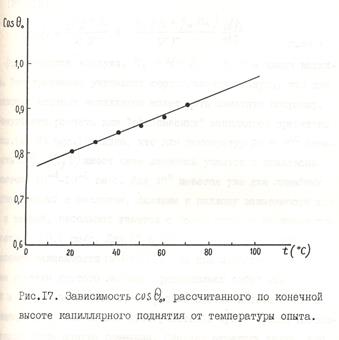 На рис. 17 приведены величины статических углов смачивания, рассчитанных по конечной высоте поднятия для разных температур. Как отмечалось ранее, для свежетянутых капилляров после кажущегося завершения процесса поднятия воды (4-6 ч.), отраженного на рис. 16а и 16б, можно наблюдать очень медленное продолжение поднятия (доли мм в сутки, т.е. < 10-6 мм/с), причиной которого, по-видимому, является постепенное регидроксилирование поверхности стекла у периметра смачивания, и, как следствие этого, уменьшение угла смачивания. Можно предполагать, что в конечном счете (за большой промежуток времени) этот процесс приведет к поднятию жидкости на высоту, соответствующую высоте поднятия в гидроксилированных капиллярах и углу смачивания, характерному для регидроксилированной поверхности стекла. Однако, поскольку скорость этого процесса чрезвычайно мала, можно предположить, что характеристической для процесса поднятия по дегидроксилированной поверхности стекла является высота поднятия за 5-6 ч. По этим высотам и были рассчитаны величины cosq, приведенные на рис. 17. В литературе имеются данные [127,220-222], показывающие, что в исследованном интервале температур угол смачивания кварца водой остается постоянным. Из рис. 17 видно, что cosq дегидроксилированной поверхности стекла линейно зависит от температуры, причем экстраполяция cosq на t = 100°С дает величину ~0,97, что соответствует значению cosq для регидроксилированного cтекла [213].
На рис. 17 приведены величины статических углов смачивания, рассчитанных по конечной высоте поднятия для разных температур. Как отмечалось ранее, для свежетянутых капилляров после кажущегося завершения процесса поднятия воды (4-6 ч.), отраженного на рис. 16а и 16б, можно наблюдать очень медленное продолжение поднятия (доли мм в сутки, т.е. < 10-6 мм/с), причиной которого, по-видимому, является постепенное регидроксилирование поверхности стекла у периметра смачивания, и, как следствие этого, уменьшение угла смачивания. Можно предполагать, что в конечном счете (за большой промежуток времени) этот процесс приведет к поднятию жидкости на высоту, соответствующую высоте поднятия в гидроксилированных капиллярах и углу смачивания, характерному для регидроксилированной поверхности стекла. Однако, поскольку скорость этого процесса чрезвычайно мала, можно предположить, что характеристической для процесса поднятия по дегидроксилированной поверхности стекла является высота поднятия за 5-6 ч. По этим высотам и были рассчитаны величины cosq, приведенные на рис. 17. В литературе имеются данные [127,220-222], показывающие, что в исследованном интервале температур угол смачивания кварца водой остается постоянным. Из рис. 17 видно, что cosq дегидроксилированной поверхности стекла линейно зависит от температуры, причем экстраполяция cosq на t = 100°С дает величину ~0,97, что соответствует значению cosq для регидроксилированного cтекла [213].
Полученные результаты позволяют предположить, что повышение температуры закономерно ускоряет процесс регидроксилирования поверхности стекла. По кривым h-t рассчитывали зависимости cosq – lg v по уравнению [25,213]
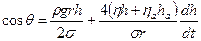 (III-73)
(III-73)
где ηa — вязкость воздуха, ha=H-h; H — длина капилляра.
Это уравнение учитывает сопротивление воздуха, что для достаточно длинных капилляров может дать заметную поправку. Результаты расчета для "равновесных" капилляров приведены на рис. 18. Из рис. 18 видно, что для температур 20 и 30°C зависимость cosq = f(lg v) имеет один линейный участок в диапазоне скоростей 10-4-10-1 см/с. Для 40°C имеется уже два линейных участка: первый с наклоном, близким к наклону зависимости для 30°C, и второй, небольшой участок с более крутым наклоном при скоростях >0,1 см/с. Для 50 и 60°C наблюдается уже четкое разделение зависимости cosq = f(lg v) на два линейных участка, причем участки крутого наклона представляют собой как бы зоны одной и той же зависимости, но разной протяженности (чем выше температура, тем больше этот участок). При 70°C зона пологого участка лишь слегка намечена. Следует отметить также, что с увеличением температуры область начала зависимости cosq от lg v сдвигается в зону больших скоростей. Обращает на себя внимание заметное отличие наклона зависимости cosq — lg v для30°C. Вполне возможно, что это отличие связано с известной аномалией воды при 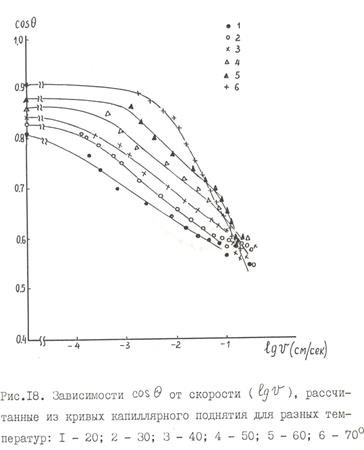 температурах вблизи 30°C [223].
температурах вблизи 30°C [223].
На рис. 19 проведено сравнение найденных зависимостей с результатами, полученными ранее. На рис. 19 приведены кривые cosq = f(lg v) "равновесных" и "неравновесных" капилляров при 20°C (Р/Рs 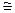 1), кривая для свежетянутых капилляров, гидроксилированных
1), кривая для свежетянутых капилляров, гидроксилированных 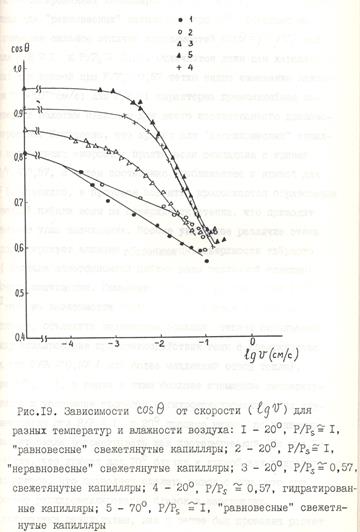 капилляров для 20°C и Р/Рs
капилляров для 20°C и Р/Рs 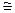 0,57 [213] и кривая для "равновесных" капилляров при 70°С. Обращает на себя внимание сильное отличие зависимостей cosq = f(lg v) при 20°C для Р/Рs
0,57 [213] и кривая для "равновесных" капилляров при 70°С. Обращает на себя внимание сильное отличие зависимостей cosq = f(lg v) при 20°C для Р/Рs 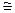 1 и Р/Рs
1 и Р/Рs 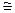 0,57. Отличается даже сам характер кривых: для кривой при Р/Рs
0,57. Отличается даже сам характер кривых: для кривой при Р/Рs 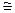 0,57 четко видно изменение наклона при v > 10-2 см/с; для Р/Рs
0,57 четко видно изменение наклона при v > 10-2 см/с; для Р/Рs 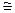 1 характерна прямолинейная зависимость с пологим наклоном для всего исследованного диапазона скоростей. Интересно, что кривая для "неравновесных" капилляров при больших скоростях практически совпадала с кривой для Р/Рs
1 характерна прямолинейная зависимость с пологим наклоном для всего исследованного диапазона скоростей. Интересно, что кривая для "неравновесных" капилляров при больших скоростях практически совпадала с кривой для Р/Рs 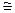 0,57, а затем постепенно приближается к кривой Р/Рs
0,57, а затем постепенно приближается к кривой Р/Рs 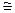 0,57. Очевидно, в процессе поднятия продолжается образование равновесной пленки воды на поверхности стекла, что приводит к изменению угла смачивания. Вообще указанное различие ярко характеризует влияние состояния поверхности твердого тела (наличие адсорбционной пленки воды различной толщины) на процесс смачивания. Изменение наклона при скоростях 10-2-10-1 см/с на зависимости cosq = f(lg v) (кривая 3) можно, по-видимому, объяснить выделением больших теплот смачивания и регидроксилирования при взаимодействии воды с поверхностью при Р/Рs
0,57. Очевидно, в процессе поднятия продолжается образование равновесной пленки воды на поверхности стекла, что приводит к изменению угла смачивания. Вообще указанное различие ярко характеризует влияние состояния поверхности твердого тела (наличие адсорбционной пленки воды различной толщины) на процесс смачивания. Изменение наклона при скоростях 10-2-10-1 см/с на зависимости cosq = f(lg v) (кривая 3) можно, по-видимому, объяснить выделением больших теплот смачивания и регидроксилирования при взаимодействии воды с поверхностью при Р/Рs 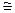 0,57 (или более медленный отвод тепла), чем при Р/Рs
0,57 (или более медленный отвод тепла), чем при Р/Рs 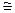 1, в связи с этим большее повышение температуры мениска и ускорение процесса регидроксилирования. Для случая смачивания при Р/Рs
1, в связи с этим большее повышение температуры мениска и ускорение процесса регидроксилирования. Для случая смачивания при Р/Рs 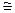 1 и 20°C процесс можно, по-видимому, во всем интервале рассматривать как изотермический. Из рис.19 видно также, что кривая для 70°C близка к кривой для гидратированных капилляров, что позволяет сделать вывод о том, что при 70°C процесс регидроксилирования близок к завершению.
1 и 20°C процесс можно, по-видимому, во всем интервале рассматривать как изотермический. Из рис.19 видно также, что кривая для 70°C близка к кривой для гидратированных капилляров, что позволяет сделать вывод о том, что при 70°C процесс регидроксилирования близок к завершению.
По полученным результатам, как и ранее был проведен расчет констант уравнения Блейка-Хэйнса, характеризующих состояние поверхности для всех исследованных температур. Результаты расчета приведены в таблице 3.
Таблица 3
Расчет констант уравнения Блейка-Хэйнса из данных
по кинетике капиллярного поднятия для свежетянутых капилляров
| t, °C | cos θ0 | Наклон прямо-линейного участка | Δn·10-18, м-2 | λ, нм | K, с-1 | ΔH·1021, Дж | ΔS·1023, Дж/К |
| 0,806 | п | 0,46 | 1,5 | 1,2·102 | 90,5 | -3,2 | |
| 0,825 | п | 0,58 | 1,3 | 7,1·102 | 90,4 | -0,7 | |
| 0,849 | п | 0,47 | 1,5 | 2,7·102 | 90,2 | -4,2 | |
| к | 1,38 | 0,9 | 8,0·104 | ||||
| 0,862 | п | 0,48 | 1,5 | 1,2·103 | 90,1 | -3,1 | |
| к | 1,07 | 1,0 | 3,5·104 | ||||
| 0,881 | п | 0,54 | 1,4 | 3,0·103 | 90,0 | -2,8 | |
| к | 1,28 | 0,9 | 8,1·104 | ||||
| 0,910 | п | 0,37 | 1,7 | 3,8·103 | 89,8 | -3,3 | |
| к | 1,11 | 1,0 | 3,5·104 |
Для 40-70°C расчет проводился по двум линейным участкам зависимости cosq — lg v:с крутым наклоном (к) и пологим наклоном (п). Из таблицы видно, что для пологих участков величины Δn, характеризующие наклон зависимости cosq — lg v близки между собой и колеблются в пределах 0,37-0,58·1018м-2, а для крутых участков 1,07-1,38·1018м-2.Последние величины близки к тому, что было получено для гидратированных капилляров и кварцевой щели (табл. 2). Величины Δn для пологих участков в 2-3 раза меньше и соответствуют, по-видимому, концентрации силанольных групп на поверхности стекла, прошедшего высокотемпературную обработку. Из литературы [78] известно, что адсорбттия воды на дегидратированной поверхности пористого стекла может уменьшаться в 2-3 раза.
При сравнении величин K для разных температур (таблица 3) обращает на себя внимание, что если величина K для пологих участков с ростом температуры увеличивается в соответствии с теорией [211], то для крутых участков она такой зависимости не имеет. Отсутствие температурной зависимости K для этих участков может, по-видимому, также говорить в пользу высказанного предположения о локальном повышении температуры зоны ТФГ для больших скоростей движения.
В соответствии с теорией абсолютных скоростей химических реакций [211]величина K в уравнении (III-67) может быть записана в следующем виде:
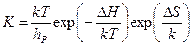 (III-74)
(III-74)
где ΔH и ΔS — энтальпия и энтропия активации смачивания соответственно.
Использование этого уравнения позволяет оценить величины ΔH и ΔS из экспериментальных данных по зависимости lg K от 1/T. При построении этой зависимости для пологих участков выяснилось, что экспериментальные точки довольно хорошо ложатся на прямую. Наклон этой прямой dlgK/d(1/T),согласно уравнению (III-74), равен (kT+ΔH)/k. Величина (kT+ΔH), называемая обычно экспериментальной энергией активации, постоянна для исследуемой системы и равна 95·10-21Дж/центр. Величины ΔH и ΔS,вычисленные для разных температур, также приведены в таблице 3.
Как видно из таблицы 3, величины энтальпии активации смачивания значительны и превышают величину энтальпии испарения (4,48·104Дж/моль). Энтальпия активации смачивания в пересчете на моль имеет в среднем значение 5,4·104Дж/моль. Величина ΔS активации смачивания имеет отрицательную величину, что говорит о разупорядочивании структуры воды на поверхности стекла в процессе смачивания.
Если предположить, что локальная температура ТФГ при больших скоростях поднятия (зоны крутого наклона зависимости cosq = f(lg v))близка к 100°C, а энтропия активации смачивания имеет ту же величину, что и для участков пологого наклона (таблица 3), то можно оценить величину энтальпии активации смачивания для участков крутого наклона по уравнению (III-74). Такой расчет дает среднюю величину ΔH=85·10-21Дж/центр, т.е. несколько меньше, чем для участков пологих наклонов.
Проведенные опыты, в соответствии с литературными данными [32], позволяют сделать вывод, что на поверхности исследованного стекла имеется по крайней мере два вида активных центров. После высокотемпературной обработки стекла один из них легко регидроксилируется в парах воды и обусловливает поведение свежетянутого стекла при малых скоростях смачивания. Концентрация этих центров соответствует величине Δn для пологих участков и характеризуется энтальпией активации ~90·10-21Дж/центр. Второй вид активных центров регидроксилируется только в результате непосредственного контакта с водой или при повышенных температурах (>70°C). Судя по наличию участка пологого наклона при малых скоростях движения ТФГ, температур 40-70°C недостаточно для регидроксилирования поверхности свежетянутого стекла в парах воды. Однако при скоростях 10-2-10-1см/с такое регидроксилирование происходит. По-видимому,как предполагалось выше, термостатирование зоны ТФГ при таких скоростях нарушается. Выделение теплоты регидроксилирования и смачивания, а также трение слоев жидкости при формировании потока локально повышает температуру зоны ТФГ >70°C (при больших скоростях не успевает проходить процесс ее выравнивания), что приводит к локальному регидроксилированию поверхности в парах и, соответственно, к уменьшению угла смачивания. При уменьшении скорости движения изотермичность процесса, по-видимому, восстанавливается.
Дата добавления: 2015-03-26; просмотров: 1197;
