Свойства гидростатического давления

Гидростатическое давление направлено всегда по внутренней нормали к площадке, на которую оно действует (рис.3.4).

Доказательство ведется от обратного утверждения.

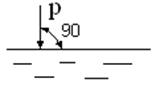Рис.3.4

Рис.3.5

Рис. 3.6

Допустим, гидростатическое давление направлено не по нормали к площадке (рис.3.5). В этом случае его можно разложить на нормальную р_n и касательную составляющие t. Появление касательной составляющей станет нарушением условия относительного покоя, т.е. частицы жидкости якобы будут перемещаться друг относительно друга.

Допустим, гидростатическое давление направлено по внешней нормали к площадке (рис.3.6). Это значило бы, что жидкость сопротивляется растягивающим усилиями, что нарушило бы принятую ранее аксиому.

Гидростатическое давление в любой точке покоящейся жидкости не зависит от направления площадки, для которой оно вычислено.

Проиллюстрируем это свойство. В жидкости на глубине h мысленно возьмем точку А (рис.3.7). Можно предположить, что давление в этой точке

будет совершенно одинаковым для направления площадок 1-1, 2-2, 3-3 и т.д., проходящих через эту точку. Докажем это очевидное свойство.

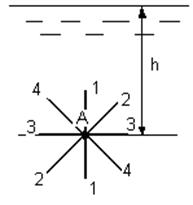
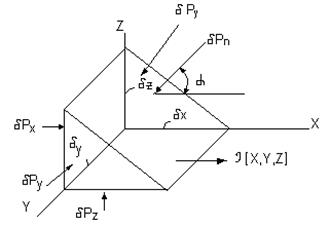
Рис. 3.7 Рис. 3.8

Для этого в жидкости, находящейся в покое, разместим оси координат и выделим в этих осях элементарный объем в виде прямоугольного клина (рис.3.8), стороны граней которого по осям равны δх, δу, δz. Применим принцип отвердевания, т.е. мысленно представим, что бесконечно малый объем превратился в твердое тело. В этом случае при рассмотрении тела в покое можно применить законы механики твердого тела, т.е. если тело находится в равновесии (покое), то сумма проекций всех сил на соответствующие оси равна нулю, т.е. ΣP_x = 0, ΣP_y = 0, ΣP_z = 0.

На выделенный объем действуют массовая сила, вызванная ускорением J, проекции которого на соответствующие оси будут равны X, Y, Z, и поверхностные силы на соответствующие грани δP_х, δP_у, δP_z, δP_п. Направление грани с индексом «n» в системе координат взято произвольно.

Составим уравнение проекции сил на ось Х:

ΣР_х = δР_х - δР_п·cosα + ХδМ = 0. (3.1)

Ввиду малости размеров граней клина будем считать, что давление на каждую из них будет одинаковым и каким-то средним, тогда

.

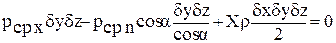Сократив на δу·δz, получим:

.

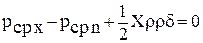В пределе, когда размеры клина будут приближаться к нулю, р_{ср x} и р_{ср n} будут стремиться к значениям гидростатического давления в точке в направлениях оси Х-Р_х и наклонной грани n – P_n, и вследствие этого при переходе к пределу при δх = 0 получаем: р_х – р_n = 0 или р_х = р_n.

Составив уравнение проекции сил на оси y и z, найдем, что р_у = р_п; р_z = р_n, откуда

P_x = P_y = P_z = P_n.. (3.2)

Последнее равенствопоказывает, что гидростатическое давление в точке покоящейся жидкости имеет значение, не зависящее от направления площадки, для которой оно вычислено.

Но гидростатическое давление в различных точках не будет одинаковым. Для разных точек давление будет являться непрерывной функцией координат.