Система показників абсолютного та відносного вимірювання ризику
| Показник | Формула розрахунку | Характеристика | |
| Абсолютне вимірювання ризику | |||
| Абсолютна величина ризику (абсолютний рівень втрат) | 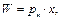 де W — величина ризику, pн — імовірність небажаних наслідків, х — величина цих наслідків
де W — величина ризику, pн — імовірність небажаних наслідків, х — величина цих наслідків
| Перевагою даного підходу є те, що в якості i-го параметра (Pі) можна використовувати широкий спектр показників, за якими підприємство прогнозує збитки у випадку реалізації певного ризику або групи ризиків | |
| Математичне сподівання | Для дискретної величини
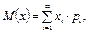 де хі — значення випадкової величини, і = 1, 2,…, рі — відповідні ймовірності.
де хі — значення випадкової величини, і = 1, 2,…, рі — відповідні ймовірності.
| Математичне сподівання, пов’язане з невизначеною ситуацією, є середньозваженим усіх можливих результатів, де ймовірність кожного з них використовується як частота або питома вага відповідного значення. | |
Для обмеженого числа (n) можливих значень випадкової величини
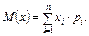 Для випадкової неперервної величини x
Для випадкової неперервної величини x
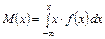 або або
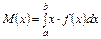 ,
якщо неперервна випадкова величина визначена на інтервалі [a, b], де f(x) — щільність ймовірності ,
якщо неперервна випадкова величина визначена на інтервалі [a, b], де f(x) — щільність ймовірності
| Сподіване значення вимірює результат, котрий середньому очікується. Імовірнісний зміст математичного сподівання конкретного параметра від проведення підприємницької діяльності полягає в тому, що воно приблизно дорівнює середньому арифметичному його можливих значень | ||
| Дисперсія | Для випадкової величини X
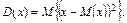 Для дискретної випадкової величини Х
Для дискретної випадкової величини Х
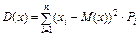 Для неперервної величини Х
Для неперервної величини Х
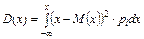 або або
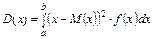
| Дисперсія — середньозважене з квадратів відхилень дійсних результатів від середніх очікуваних. Характеризує розсіювання значення випадкового параметра від його середнього прогнозованого значення | |
| Середньоквадратичне відхилення | 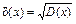
| Показує максимально можливе коливання певного параметра від його се- редньоочікуваної величини та дає можливість оцінити ступінь ризику з погляду ймовірності його здійснення (чим більша величина даної числової характеристики, тим ризикованішим є господарське рішення) | |
Семіваріація
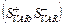
| 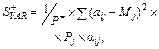 де Р+= — сумарна ймовірність настання тих зовнішньоекономічних умов, які дають ймовірність, більшу від середнього значення
де Р+= — сумарна ймовірність настання тих зовнішньоекономічних умов, які дають ймовірність, більшу від середнього значення
| Додатна семіваріація характеризує дисперсію тих значень прибутку, які більші від середнього. Чим більше значення вона має, тим більшим є очікуваний від варіанту рішення прибуток. Від’ємна семіваріація характеризує дисперсію тих значень прибутку, які менші від середнього. Чим менше від’ємна семіваріація, тим менші очікувані втрати | |
Семіквадратичне відхилення
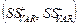
| 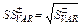
| Додатне семіквадратичне відхилення абсолютного значення сподіваного прибутку; показує абсолютну відстань, на якій знаходиться значення прибутку, більше від середнього (математичного сподівання). Чим більше значення показника, тим більший ризик. Від’ємне семіквадратичне відхилення характеризує відхилення абсолютного значення очікуваних втрат (можливе збільшення втрат). Чим більше значення показника, тим менший ризик | |
Продовження табл. 7.16
| Показник | Формула розрахунку | Характеристика | |
| Відносне вимірювання ризику | |||
| Величина ризику у відносному вираженні | Розмір збитків, віднесений до конкретної бази, обраної безпосередньо підприємством, залежно від специфіки та виду оцінюваного ризику | Базою віднесення збитків можуть виступати: витрати на виробництво, вартість основних виробничих фондів, активи підприємства, прибуток, чисельність персоналу, вартість окремих ресурсів і т. д. | |
| Вибір тієї або іншої бази не має принципового значення, але необхідно віддавати перевагу показнику, що має високий ступінь достовірності | |||
| Коефіцієнт варіації K(х)VAR | 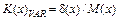 ,
де δ(х) — середньоквадратичне відхилення доходів,
M(x) — величина сподіваних доходів ,
де δ(х) — середньоквадратичне відхилення доходів,
M(x) — величина сподіваних доходів
| Порівнює ризикованість напрямів діяльності і конкретних ситуацій за ознаками (втратами), вираженими у різних одиницях виміру. Коефіцієнт варіації може змінюватися в межах від 0 до 100 %. Чим менша величина, тим більш стабільною є прогнозована ситуація і, відповідно, менший ступінь ризику здійснення напряму діяльності чи певного заходу | |
| Коефіцієнт ризику (KR) | 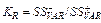
| Чим більше значення, тим більшим є ступінь ризику варіанту рішення | |
Оцінювання господарського ризику передбачає необхідність побудови кривої ризику — кривої розподілу ймовірностей виникнення певного рівня втрат/прибутку. Це надзвичайно складна задача, тому на практиці доводиться обмежуватися спрощеними підходами, оцінюючи ризик за одним або кількома показниками. Процес побудови кривої ризику, як правило, включає такі етапи:
1) встановлення зон ризику, в рамках яких утрати не перевищують визначеного рівня;
2) визначення залежності ймовірності утрат від їх рівня;
3) побудова типової кривої ймовірностей одержання певного рівня прибутку;
4) побудова кривої ризику на основі кривої ймовірностей отримання певного рівня прибутку та зон ризику.
На рис. 7.3 схематично показано основні зони ризику, які повинні враховуватися під час оцінки ризику конкретного виду діяльності.
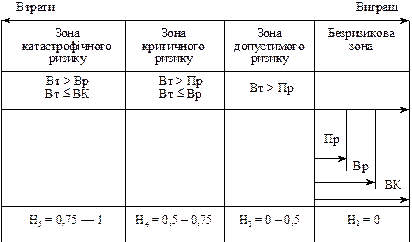
Рис. 7.3. Основні зони ризику підприємницької діяльності*
Наступним етапом у процесі оцінювання ризикованих ситуацій є встановлення залежності ймовірності втрат від їх рівня. Розглянемо прибуток як випадкову величину та побудуємо спочатку криву розподілу ймовірностей одержання певного рівня прибутку (рис. 7.4).
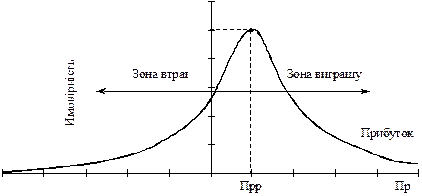
Рис. 7.4. Типова крива ймовірностей одержання певного рівня прибутку
При цьому слід дотримуватися таких припущень:
Ø найбільш імовірним є отримання прибутку, що дорівнює його очікуваній величині (Прр); за результатами багаторічних спостережень така ймовірність на промислових підприємствах становить переважно від 0,8 до 0,95; імовірність (Ір) отримання прибутку максимальна, відповідно значення (Прр) можна вважати математичним сподіванням прибутку. Ймовірність прибутку, більшого або меншого порівняно з розрахунковим тим нижча, чим більше такий прибуток відрізняється від розрахункового, тобто значення ймовірності відхилення від розрахункового прибутку монотонно спадають за зростання відхилень;
Ø імовірність винятково великих (теоретично нескінченних) втрат практично дорівнює нулю, оскільки втрати явно мають верхню межу (не враховуються витрати, які неможливо кількісно оцінити);
Ø втратами прибутку (ΔПр) вважається його зменшення порівняно з розрахунковою величиною Прр. Якщо реальний прибуток дорівнює Пр, то ΔПр = Прр – Пр.
Хоча прийняті припущення певною мірою відносні (можуть не дотримуватися для всіх видів господарських ризиків), проте здебільшого вони правильно відображають закономірності зміни підприємницького ризику. При цьому такі припущення базуються на підході, згідно з яким прибуток, як випадкова величина, підпорядкований нормальному або близькому до нормального закону розподілу з погляду ймовірності одержання певної його суми.
На основі кривої ймовірностей отримання певного рівня прибутку та зон ризику побудуємо криву ризику (рис. 7.5). Фактично це та сама крива, але побудована в іншій системі координат.
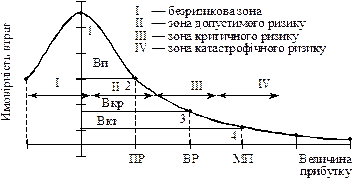
Рис. 7.5. Крива ризику*
Для побудови кривої ризику обмежимося даними про ймовірність виникнення втрат у точках 1, 2, 3, 4. Здобуттю більш точного результату сприяє визначення проміжних величин ймовірності появи витрат. Слід зауважити, що частота виникнення певних утрат, інтенсивність, форма кривої ризику на графіку будуть різними відповідно для виробничого, комерційного, фінансового та валютного ризиків.
Прийняття остаточного рішення щодо здійснення конкретного підприємницького проекту вимагає визначення граничного рівня господарського ризику. Можна орієнтуватися на такі показники, як 0,1, 0,01 та 0,001 відповідно для допустимого, критичного та катастрофічного ризиків. Але специфічність умов функціонування будь-якого підприємства зумовлює різні значення граничного показника [46].
Дата добавления: 2015-03-20; просмотров: 2422;
