Предмет и метод вычислительной математики
Область математики, которая призвана разрабатывать методы доведения до числового результата основных задач математического анализа, алгебры, геометрии и т.д. и пути использования для этой цели современных вычислительных средств, называется вычислительной математикой.
Большинство задач математики могут быть записаны в виде:
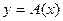 , (1)
, (1)
где 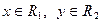 ,
, 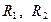 - заданные пространства,
- заданные пространства, 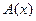 - некоторая заданная функция. Задача состоит либо в отыскании
- некоторая заданная функция. Задача состоит либо в отыскании 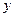 по заданному
по заданному 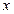 , либо в отыскании
, либо в отыскании 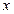 по заданному
по заданному 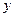 .
.
Далеко не всегда с помощью средств современной математики удается точно решить эти задачи, применяя конечное число шагов. В этих случаях прибегают к вычислительной математике, в задачи которой входит и разработка приемов и методов наиболее рационального решения конкретных задач.
Одним из основных методов, при помощи которого в вычислительной математике решают поставленные задачи, является замена пространств 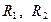 и функции
и функции 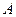 некоторыми другими пространствами
некоторыми другими пространствами 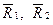 и функцией
и функцией 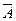 , более удобными для вычислительных целей. Иногда бывает достаточно произвести замену
, более удобными для вычислительных целей. Иногда бывает достаточно произвести замену 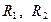 или даже одного из них. Иногда достаточно заменить только функцию
или даже одного из них. Иногда достаточно заменить только функцию 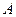 . Замена должна быть сделана так, чтобы решение новой задачи
. Замена должна быть сделана так, чтобы решение новой задачи
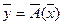 (2)
(2)
где 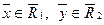 , было в каком-то смысле близким к точному решению исходной задачи (1) и его возможно было бы практически отыскать с сравнительно небольшими трудностями.
, было в каком-то смысле близким к точному решению исходной задачи (1) и его возможно было бы практически отыскать с сравнительно небольшими трудностями.
Например, пусть необходимо вычислить интеграл Римана 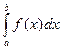 , где
, где 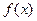 - произвольная непрерывная на сегменте
- произвольная непрерывная на сегменте 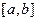 функция (т.е. она интегрируема по Риману на
функция (т.е. она интегрируема по Риману на 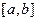 ), но первообразная для нее в элементарных функциях не берется. В обозначения задачи (1): исходные данные – функция
), но первообразная для нее в элементарных функциях не берется. В обозначения задачи (1): исходные данные – функция 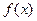 , она принадлежит пространству непрерывных на
, она принадлежит пространству непрерывных на 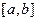 функций -
функций - 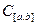 , т.е.
, т.е. 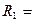
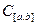 . По функции нужно определить число
. По функции нужно определить число 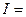
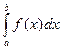 ,
, 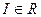 , т.е.
, т.е. 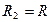 . Функция, которая исходным данным ставит в соответствие числовой результат, это функция интегрирования по Риману на
. Функция, которая исходным данным ставит в соответствие числовой результат, это функция интегрирования по Риману на 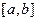 , т.е. в обозначениях (1):
, т.е. в обозначениях (1): 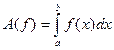 . Для решения этой задачи возможны 2 пути:
. Для решения этой задачи возможны 2 пути:
1. Заменить функцию 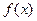 алгебраическим многочленом
алгебраическим многочленом 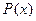 равномерно приближающим функцию
равномерно приближающим функцию 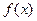 на
на 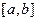 с необходимой степенью точности (рис.1) (как будет показано позже, это можно сделать). Затем вместо
с необходимой степенью точности (рис.1) (как будет показано позже, это можно сделать). Затем вместо 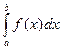 находится
находится 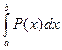 , вычисление которого не составляет труда. Конечно
, вычисление которого не составляет труда. Конечно
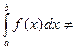
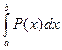 ,
,
но если 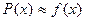 , то
, то 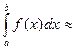
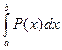 .
.
Произведенная замена исходной задачи включает в себя только замену пространства исходных данных 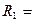
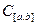 на
на 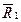 - пространство многочленов: вместо функции
- пространство многочленов: вместо функции 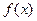 для интегрирования берется многочлен
для интегрирования берется многочлен 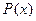 из некоторой ее окрестности.
из некоторой ее окрестности.
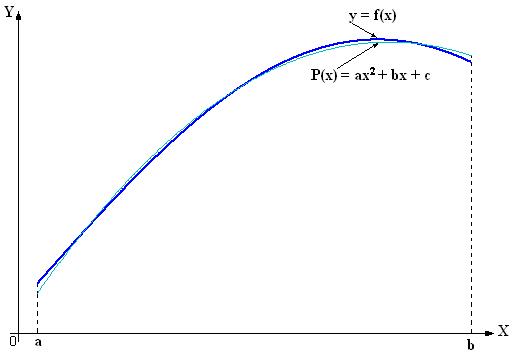
Рис.1.
2. Из определения 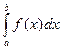 следует, что всегда можно построить интегральную сумму
следует, что всегда можно построить интегральную сумму
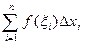 ,
,
которая будет достаточно близка к значению интеграла (рис.2): 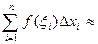
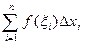 .
.
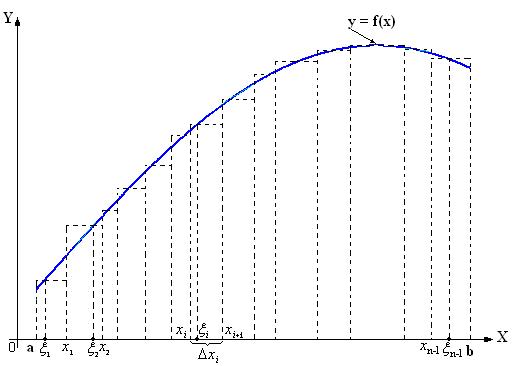
Рис.2.
Таким образом задача вычисления интеграла заменена на другую задачу – вычисления конечной суммы, а это значит, что при неизменности пространств 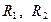 произошла замена функции
произошла замена функции 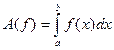 новой функцией
новой функцией 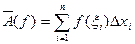 .
.
Задание 1.1. Привести примеры задач, для решения которых используется метод замены.
Дата добавления: 2015-03-20; просмотров: 885;
