В дальнейшем по тексту под термином «объект» необходимо подразумевать СИ, СИспыт., СКонтр.
При изготовлении объекта его надёжность обеспечивается технологией производства. Она зависит от качества изготовленных деталей, методов контроля выпускаемой продукции, возможностей управления ходом технологического процесса, от качества сборки объекта и его узлов, методов испытаний готовой продукции и других показателей технологического процесса.
При эксплуатации объекта его надёжность реализуется. Она зависит от методов и условий эксплуатации объекта.
Базу науки о надёжности составляют:
- математические методы теории надёжности, включающие в основном теорию вероятностей и математическую статистику, методы оптимизации, теорию информации и математическую логику и др.;
- теория повреждающих процессов, изучающая физико-химические процессы, приводящие к потере начальных свойств при эксплуатации объекта, прежде всего, - триботехнические процессы, усталость, коррозию, эрозию и старение;
- прикладные методы обеспечения надёжности в областях расчета, проектирования, технологии изготовления, эксплуатации и ремонта объектов изучаемого типа.
Основные понятия и термины теории надёжности стандартизованы. В ней рассматриваются следующие обобщенные объекты.
Изделие – единица продукции, выпускаемая предприятием, которая может состоять из одной детали или совокупности деталей, например, механизм, прибор и т.д.
Элемент изделия – составная часть изделия, предназначенная для выполнения его определенных функций.
Система изделия – совокупность совместно действующих элементов, предназначенная для самостоятельного выполнения заданных функций.
Для однозначности формулировок объектом будем определять понятие, обобщающее в себе элемент, систему и изделие.
Объекты подразделяются на невосстанавливаемые, для которых проведение восстановления работоспособного состояния не предусмотрено в нормативно-технической и (или) конструкторской документации, и они подлежат замене (радиоэлементы, микросхемы, уплотнения, подшипники и т.п.), и восстанавливаемые, для которых такое восстановление предусмотрено.
Надёжность объектов характеризуется перечисленными ниже основными состояниями.
Исправное состояние – состояние объекта, при котором он соответствует всем требованиям нормативно-технической и (или) конструкторской (проектной) документации.
Неисправное состояние – состояние объекта, при котором он не соответствует хотя бы одному из требований нормативно-технической и (или) конструкторской (проектной) документации.
Работоспособное состояние – состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствует требованиям нормативно-технической и (или) конструкторской (проектной) документации.
Неработоспособное состояние – состояние объекта, при котором значение хотя бы одного параметра, характеризующего способность выполнять заданные функции, не соответствует требованиям нормативно-технической и (или) конструкторской (проектной) документации. При этом для сложных объектов из множества неработоспособных состояний выделяют частично неработоспособные состояния, при которых объект способен частично выполнять требуемые функции.
Предельное состояние – состояние объекта, при котором его дальнейшая эксплуатация недопустима или нецелесообразна, либо восстановление его работоспособного состояния невозможно или нецелесообразно. При этом критериями предельного состояния объекта являются признак или совокупность признаков, установленные нормативной документацией (НД), технологической и (или) конструкторской (проектной) документацией.
В надёжности машин вообще, а СИ, СИспыт. и СКонтр. в частности, как составляющие машин, основными событиями являются:
- повреждение – событие, заключающееся в нарушении исправного состояния объекта при сохранении работоспособного состояния;
- отказ – событие, заключающееся в нарушении работоспособного состояния объекта.
Поскольку основным предметом теории надёжности является прогнозирование и обеспечение работоспособности технических систем, дальнейший анализ будет проведен применительно к отказам.
Отказы подразделяются на отказы функционирования, при которых выполнение функций объектом прекращается, и параметрические, при которых хотя бы один параметр объекта изменяется в недопустимых пределах.
Причины отказов делятся на случайные и систематические.
Случайные причины - это непредусмотренные перегрузки, дефекты материала и погрешности изготовления, не обнаруженные контролем, ошибки обслуживающего персонала и разного рода нештатные ситуации.
Систематические причины - это закономерные явления, вызывающие постепенное накопление повреждений и отказов. Это коррозия, старение, усталость, ползучесть, изнашивание, эрозия, т.е. повреждающие (деградационные) процессы.
ГОСТ 27.002-89 предписывает классифицировать отказы по признакам, приведенным в таблице 11.1. По своим последствиям отказы могут быть легкими – легкоустранимыми, средними – не вызывающими разрушений других узлов, и тяжелыми – вызывающими вторичные разрушения или жертвы.
По возможности дальнейшего использования объекта, отказы надёжности подразделяют на полные, исключающие использование объекта до устранения отказа, и частичные, при которых объект может ограниченное время использоваться. Отказы также подразделяют на устранимые, причины возникновения которых известны и могут быть полностью устранены, что исключает их возникновение при дальнейшей эксплуатации, и неустранимые, причины возникновения которых не могут быть устранены для объектов данного вида.
Таблица 11.1 – Классификационные признаки отказов
| Термин | Определение |
| Ресурсный отказ | Отказ, в результате которого объект достигает предельного состояния |
| Независимый отказ | Отказ, не обусловленный другими отказами |
| Зависимый отказ | Отказ, обусловленный другими отказами |
| Внезапный отказ | Отказ, характеризующийся скачкообразным изменением значений одного или нескольких параметров объекта |
| Постепенный отказ | Отказ, возникающий в результате постепенного изменения значений одного или нескольких параметров объекта |
| Сбой | Самоустраняющийся отказ или однократный отказ, устраняемый незначительным вмешательством оператора |
| Перемежающийся отказ | Многократно возникающий самоустраняющийся отказ одного и того же характера |
| Явный отказ | Отказ, обнаруживаемый визуально или штатными методами и средствами контроля и диагностирования при подготовке объекта к применению или в процессе его применения по назначению |
| Скрытый отказ | Отказ, не обнаруживаемый визуально или штатными методами и средствами контроля и диагностирования, но выявляемый при проведении технического обслуживания или специальными методами диагностики |
| Продолжение таблицы 11.1 | |
| Конструктивный отказ | Отказ, возникающий по причине, связанной с несовершенством или нарушением установленных правил и (или) норм проектирования и конструирования |
| Производственный отказ | Отказ, возникающий по причине, связанной с несовершенством или нарушением установленного процесса изготовления или ремонта, выполняемого на ремонтном предприятии |
| Эксплуатационный отказ | Отказ, возникающий по причине, связанной с нарушением установленных правил и (или) условий эксплуатации |
| Деградационный отказ | Отказ, обусловленный естественными процессами старения, изнашивания, коррозии и усталости при соблюдении всех установленных правил и (или) норм проектирования, изготовления и эксплуатации |
По времени возникновения отказы надёжности делятся на приработочные, возникающие в первый период эксплуатации; при нормальной эксплуатации, характеризуемой практически постоянной или незначительной изменяющейся интенсивностью отказов, и износовые. Названным временным интервалам соответствуют три явно выраженных участка кривой изменения интенсивности отказов, представленной на рисунке 11.1.
Обычно в расчетах надёжности первый участок кривой не учитывают; расчеты производятся, начиная со второго участка. На третьем участке, называемом периодом старения или износа, происходят необратимые физико-химические изменения, когда интенсивность отказов монотонно возрастает и надёжность соответственно снижается.
Основные показатели надёжности
Надёжность объекта является его интегральным свойством, формируемым такими комплексными составляющими, как безотказность, долговечность, ремонтопригодность и сохраняемость.
Безотказность – свойство объекта непрерывно сохранять работоспособность в течение заданного времени или наработки. Это свойство особенно важно для объектов, отказ в работе которых связан с опасностью для жизни людей, остановкой сложного производства или производства с непрерывным технологическим циклом.
Долговечность – свойство объекта длительно сохранять работоспособность до наступления предельного состояния, то есть в течение всего периода эксплуатации при установленной системе технических обслуживаний и ремонтов.

Р(t) – вероятность безотказной работы; f(t) – плотность распределения отказов; l(t) – интенсивность отказов.
Рисунок 11.1 – Типичные формы кривых, характеризующие безотказность элементов.
Для невосстанавливаемых объектов понятия безотказности и долговечности практически совпадают.
Ремонтопригодность - свойство объекта, которое заключается в его приспособленности к предупреждению и обнаружению причин возникновения отказов, а также поддержанию и восстановлению работоспособности с помощью технических обслуживаний и ремонтов.
Сохраняемость- свойство объекта сохранять значения показателей безотказности, долговечности и ремонтопригодности в течение и после хранения и (или) транспортирования. Практическая роль этого свойства особенно важна для приборов и прецизионных деталей, а так же многих объектов одноразового использования, для которых характерен значительный промежуток времени между изготовлением и началом использования, например, средства вооружения.
Каждый из перечисленных показателей надёжности имеет свои дифференцированные показатели, имеющие вероятностную природу.
Показатели для оценки безотказности
Основным показателем является вероятность безотказной работы Р(t) – вероятность того, что в пределах заданной наработки отказа объекта не произойдет. Данный показатель определяется по формуле (11.15):
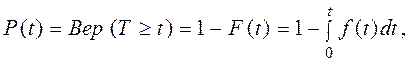 (11.15)
(11.15)
где “Вер” - вероятность события;
Р(t), F(t)- интегральные функции распределения соответственно вероятностей безотказной работы и наступления отказа для наработки t;
0<Р(t)<1.
Вероятность противоположного события называется вероятностью отказа. Она дополняет вероятность безотказной работы до единицы и определяется по формуле (11.16):
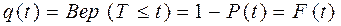 , (11.16)
, (11.16)
Например, если вероятность безотказной работы объекта в течение T=1000ч равняется 0,95, то это означает, что из большого количества СИ в среднем около 5% СИ теряют свою работоспособность раньше, чем через 1000 ч работы.
Показатель P(t) может быть применим и для оценки безотказности одного объекта. В этом случае он определяет способность объекта проработать без отказов заданный период времени.
Необходимо иметь ввиду, что применение Р(t) без указания периода времени t = Т, в течение которого рассматривается работа изделия, некорректно.
На рисунке 11.3 показана зависимость вероятности безотказной работы Р(t) и отказа F(t) объекта от времени его эксплуатации (наработки).

Рисунок 11.3 – Зависимость вероятности безотказной работы объекта от наработки.
Кривые пересекаются в точке, соответствующей среднему сроку службы объекта t = Tср, при котором P(t) = q(t) = 0,5.
Показатель удобен в том случае, когдаР(t) → 1, то есть отказ – редкое событие. В том же случае, когда отказы легко устранимы и не приводят к каким-либо значительным последствиям и Р(t) → 0, более наглядным показателем безотказности является параметр потока отказов w(t) – отношение среднего числа отказов объекта за произвольно малую его наработку к значению этой наработки. Параметр потока отказов можно вычислить по формуле (11.17):
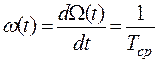 , (11.17)
, (11.17)
где Ω(t) - среднее число отказов за время t; Тср - наработка на отказ - отношение суммарной наработки изделия к числу отказов, возникших за этот период, т.е. средняя продолжительность безотказной работы объекта.
Таким образом, параметр потока отказов - это среднее количество отказов объекта в единицу времени.
Для невосстанавливаемых и восстанавливаемых объектов понятие наработки различается: в первом случае подразумевается наработка до первого отказа (он же является и последним), во втором – между двумя соседними во времени отказами (после каждого отказа производится восстановление работоспособного состояния).
Математическое ожидание случайной наработки является характеристикой безотказности и называется средней наработкой на отказ (между отказами) и определяется по формуле (11.18):
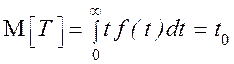 , (11.18)
, (11.18)
где t - текущее значение наработки;f(t) – плотность вероятности ее распределения.
Средняя наработка на отказ – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки.
Средняя наработка до отказа 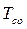 - это математическое ожидание наработки T до отказа невосстанавливаемого объекта. Вычисляется по формуле (11.19):
- это математическое ожидание наработки T до отказа невосстанавливаемого объекта. Вычисляется по формуле (11.19):
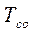
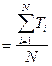 , (11.19)
, (11.19)
где N - количество исследуемых объектов.
Для оценки безотказности невосстанавливаемых объектов используется и такой показатель, как интенсивность отказовl– условная плотность вероятности отказа невосстанавливаемого объекта, определяемая для рассматриваемого момента времени при условии, что до этого времени отказ не возник. Показатель определяется по формуле (11.20) и равен отношению среднего числа объектов, отказавших в единицу наработки Nотк, к числу объектов, оставшихся работоспособными Nраб:
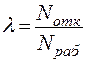 (11.20)
(11.20)
Сравнительно реже в практике используются следующие показатели безотказности:
- гамма – процентная наработка до отказа - наработка, в течение которой отказ объекта не возникает с вероятностью 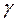 , выраженной в процентах;
, выраженной в процентах;
- осредненный параметр потока отказов – отношение математического ожидания числа отказов восстанавливаемого объекта за конечную наработку к значению этой наработки.
Показатели для оценки долговечности
Сохранение работоспособности объекта за весь период его эксплуатации до наступления предельного состояния оценивается следующими показателями.
Ресурс - наработка объекта от начала эксплуатации или возобновления эксплуатации после ремонта до предельного состояния. Наработка есть продолжительность или объем работы объекта, поэтому ресурс исчисляется в единицах времени работы (моточас), длины пути (километр), единицах выпуска продукции (штука - для технологического оборудования) и других показателях реальной наработки. Для невосстанавливаемых объектов понятия ресурса и наработки до отказа совпадают.
Срок службы - календарная наработка объекта до наступления предельного состояния. Обычно выражается в годах или месяцах.
Гамма - процентный ресурс характеризует наработку, в течение которой объект не достигает предельного состояния надёжности с заданной вероятностью γ, выраженной в процентах.
Аналогично определяется гамма - процентный срок службы.
Показатели для оценки ремонтопригодности
Время восстановления – продолжительность восстановления работоспособного состояния объекта.
Среднее время восстановленияработоспособностиобъекта 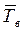 – математическое ожидание времени восстановления работоспособного состояния, определяемое по формуле (11.21):
– математическое ожидание времени восстановления работоспособного состояния, определяемое по формуле (11.21):
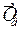 =
= 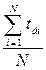 , (11.21)
, (11.21)
где 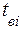 - продолжительность восстановления одного объекта;
- продолжительность восстановления одного объекта;
N - количество объектов.
Вероятность восстановления работоспособности в заданные сроки Рв– вероятность того, что время восстановления работоспособности объекта не превысит заданного. Она вычисляется по формуле (11.22):
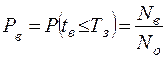 , (11.22)
, (11.22)
где tв - время восстановления;Тз- заданное время восстановления;Nв - количество объектов, восстановленных за время, меньшее заданного;Nо - общее количество объектов.
Для оценки ремонтопригодности машин в качестве показателей также применяются:
- гамма - процентное время восстановления – время, в течение которого восстановление работоспособности объекта будет осуществлено с вероятностью 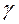 , выраженной в процентах;
, выраженной в процентах;
- интенсивность восстановления – условная плотность вероятности восстановления работоспособного состояния объекта, определенная для рассматриваемого момента времени при условии, что до этого момента восстановление не было завершено;
- средняя трудоемкость восстановления – математическое ожидание трудоемкости восстановления объекта после отказа.
Показатели для оценки сохраняемости
Средний срок сохраняемости – математическое ожидание срока сохраняемости.
Гамма - процентный срок сохраняемости – срок сохраняемости, достигаемый объектом с заданной вероятностью γ, выраженной в процентах.
Обобщающие показатели надёжности
Обобщающие показатели применяются для анализа надёжности сложных технических систем. В практике анализа надёжности применяют коэффициент технического использования, коэффициент готовности и коэффициент оперативной готовности.
Коэффициент технического использования Kти – отношение математического ожидания интервалов времени пребывания объекта в работоспособном состоянии 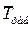 за некоторый период эксплуатации к сумме математических ожиданий интервалов времени пребывания объекта в работоспособном состоянии и простоев, связанных с проведением технических обслуживаний и ремонтов за этот же период эксплуатации Tрем.i. Коэффициент технического использования определяется по формуле (11.23):
за некоторый период эксплуатации к сумме математических ожиданий интервалов времени пребывания объекта в работоспособном состоянии и простоев, связанных с проведением технических обслуживаний и ремонтов за этот же период эксплуатации Tрем.i. Коэффициент технического использования определяется по формуле (11.23):
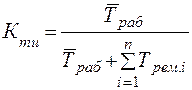 , (11.23)
, (11.23)
где n - количество технических обслуживаний и ремонтов.
Коэффициент технического использования является безразмерной величиной (0 <Кти< 1). Он численно равен вероятности того, что в данный момент времени объект работает, а не ремонтируется или обслуживается.
Коэффициент технического использования, взятый за период между плановыми ремонтами и техническим обслуживанием, называется коэффициентом готовности.
Коэффициент готовности Kг учитывает непредусмотренные остановки объекта, наличие которых свидетельствует о том, что плановые ремонты и мероприятия по техническому обслуживанию не полностью выполняют свою роль. Он численно равен вероятности того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых эксплуатация объекта не предусматривается. Коэффициент готовности вычисляется по формуле (11.24):
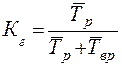 , (11.24)
, (11.24)
где 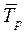 - среднее время нахождения в работоспособном состоянии;
- среднее время нахождения в работоспособном состоянии; 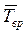 - среднее время нахождения во внеплановом ремонте.
- среднее время нахождения во внеплановом ремонте.
Коэффициент готовности количественно характеризует одновременно два показателя – безотказность и ремонтопригодность.
Коэффициент оперативной готовности - вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых эксплуатация объекта не предусматривается, и, начиная с этого момента, будет работать безотказно в течение заданного интервала времени.
Конструкция современной измерительной системы состоит из тысяч отдельных деталей, и каждая из них должна безотказно функционировать в течение заданных промежутков времени, величины которых зависят от назначенных и реально обеспечиваемых показателей надёжности – безотказности, долговечности, ремонтопригодности и сохраняемости.
Варьируя известными показателями надёжности составных частей, сформируем методику оценки сложной системы (СС).
Для решения поставленной задачи необходимо иметь идеализированное представление о СС как совокупности элементов, находящихся в определенном соотношении, иначе говоря, разработать расчетную схему. Последняя в основном определяется постановкой задачи, особенностями конструкции СС и правилами ее эксплуатации.
Под элементом СС следует понимать составную часть ее конструкции, которая может характеризоваться собственными входными и выходными параметрами и рассматривается как неделимая.
Выходной параметр характеризует и обобщает результаты протекания повреждающих процессов при использовании изделия по назначению.
Выбор конкретного критерия для включения элементов в расчетную схему зависит от постановки задачи, определения математических, физико-химических и технических возможностей моделирования и назначения адекватной модели.
С целью минимизации уровня сложности расчетной схемы элементы объединяют в 5 групп:
- элементы, отказы которых практически не влияют на работоспособность и выходные параметры СС;
- элементы, работоспособность которых за рассматриваемый промежуток времени практически не изменяется;
- элементы, для которых контроль технического состояния, ремонт и техническое обслуживание возможно осуществить, не прерывая типового рабочего цикла использования СС по назначению;
- элементы, отказы которых за рассматриваемый период времени могут привести к постепенным отказам СС;
- элементы, которые одновременно имеют ограниченнуюконтролепригодность в эксплуатации, подвержены отказам, приводящим к возникновению нештатных ситуаций, и могут быть изъяты из СС только в стационарных условиях с использованием специального оборудования.
В расчетную схему следует включить элементы пятой и, в отдельных случаях, четвертой групп. В итоге расчетная схема будет содержать необходимое и достаточное количество элементов.
Многообразие вариантов связей между элементами СС и их влияние на выходные параметры моделируют структурной функцией. Под структурой далее подразумевается формальное отображение указанных связей.
Если система состоит из элементов, выходные параметры которых не участвуют в формировании любого из выходных параметров системы, а изменение выходного параметра такого элемента не влияет на работу других элементов, то в этом случае мы имеем систему с расчленяемой структурой.
Для системы со связанной структурой характерны следующие случаи взаимодействия элементов:
- выходной параметр элемента участвует в формировании одного или группы выходных параметров системы;
- выходной параметр элемента влияет на состояние других элементов, для которых его применение эквивалентно изменению определяющих условий функционирования.
Для конструкции большинства СС характерна комбинированная структура,т.е. наличие подсистем со связанными расчлененными структурами.
В исследованиях надёжности технических систем, различных по назначению и принципу функционирования, весьма удобно использовать математические модели, сформированные на основе теории графов. С помощью графов можно описывать структуру многих технических систем, находить показатели надёжности, строить модели надёжности систем, которые изначально не имеют сетевой структуры.
Графом называется совокупность вершин (узлов) и ребер, связанных между собой, т.е. это такая абстрактная математическая система, которая состоит из двух множеств — вершин и ребер и отображения множества вершин имножества ребер. Различные узлы графа связаны между собой (не обязательно все) ребрами. На рисунке 11.4 представлен пример графа, состоящего из 3 вершин и 4 ребер.
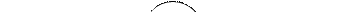
Рисунок 11.4 – Пример графа.
В каждый узел может входить или из узла может выходить несколько ребер. В этом случае говорят о множестве ребер, инцидентных данному узлу графа. Каждому ребру инцидентны два узла, расположенные на его концах. Сами ребра могут быть простыми (ребра 3, 4) и кратными (ребра 1, 2), направленными (ребро 3) и ненаправленными (ребра 1, 2, 4). Кратные ребра — это несколько (как правило, идентичных) ребер, инцидентных одной и той же паре вершин. В противном случае ребра называются простыми.
Направленные ребра иногда называются дугами. Если по ненаправленному ребру допускается идентичная связь от одной вершины к другой, то для направленного ребра (дуги) один из узлов является источником, а второй — стоком, и передача потока в обратном направлении по дуге невозможна.
Если в конечном графе, т.е. в графе, включающем конечное число вершин, из любой вершины через конечное число ребер (или дуг) можно попасть в любую другую вершину, то говорят о связности графа. Рассмотрим, как эти абстрактные понятия теории графов находят свое применение в прикладных задачах надёжности.
Имеются две альтернативные методики определения метода показателей надёжности. Одна из них - методы анализа влияния отказов, когда осуществляется оценка воздействия повреждения отдельных элементов на поведение системы, вторая - анализ деревьев отказов, позволяющий выявить причины возможных отказов.
Когда проводится анализ влияния отказов для некоторой подсистемы, которая входит как составная часть в более общую систему, необходимо установить виды отказов отдельных элементов подсистемы. Определяется, какие последствия имеют отказы отдельных элементов на всю подсистему. При этом целесообразно начинать анализ с функций, которые должны выполняться соответствующими составными частями. Далее определяется, при каких обстоятельствах наступает отказ данного вида. От этого зависит, будет ли наступивший отказ обнаружен сразу или он может остаться вначале незамеченным. Следует также выяснить, как влияют те или иные виды отказов на систему более высокого ранга.
В исследованиях надёжности сложных систем часто рекомендуется комбинация анализа деревьев отказов с методом анализа влияния отказов. При этом для определенных «критических событий» удается определить как их возможные последствия, так и их возможные причины.
Причинно-следственная диаграмма для некоторого определенного «критического события», например, превышения давлением или температурой предельного допустимого значения, позволяет, с одной стороны, выявить его причины (диаграмма причин), а с другой стороны - все возможные последствия (диаграмма последствий). Диаграмма причин интерпретируется как дерево отказов, причём «критические события» играют роль отказов системы. Диаграмма последствий представляет собой дерево решений и рисков, описывающее различные последствия отказов, к которым приводят критические события в случае неуспеха защитных мероприятий.
Наиболее распространённым способом представления СС являются двух-полюсные схемы, формируемые по принципу вход (полюс 1) – выход (полюс 2).
Системы подразделяются на последовательные, параллельные и комбинированные. Последовательной системой называется такая система, которая работоспособна только в том случае, если работоспособны все ее элементы. Если вместо работоспособности говорить о состоянии отказа, то последовательная система отказывает, если отказывает ходя бы один ее элемент.
Здесь в качестве примера рассмотрим более длинную последовательную систему, например, электронный блок системы навигации (БСН), содержащий следующие подсистемы (элементы): высокочастотный приёмно-передающий блок с антенной (Н), блок предварительного усиления (М), генератор (О), блок усиления промежуточной частоты (Z), демодулятор (D), монитор (N), источник питания (S), корпус (G).
Буквы в скобках условно обозначают случайные события — работоспособные состояния элементов. Событие, соответствующее отказу элемента, помечается чертой сверху, т.е. ( 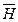 ), (
), (  ), (
), ( 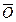 ), (
), (  ), (
), ( 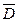 ), (
), ( 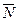 ), (
), ( 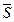 ), (
), (  ).
).
Очевидно, для того, чтобы наступило желаемое событие (обозначаемое здесь R) - «БСН работоспособен», необходимо чтобы наступили все перечисленные события.
Эту взаимосвязь можно изобразить с помощью расчетной схемы надёжности БСН по критерию работоспособности (Рисунок 11.5). Путь, соединяющий исходный узел А с конечным узлом Е на схеме расчета надёжности, существует только тогда, когда работоспособны все элементы.

Рисунок 11.5 - Схема расчета надёжности БСН по критерию работоспособности.
Схема расчета надёжности БСН по критерию отказа на на рисунке 11.6.
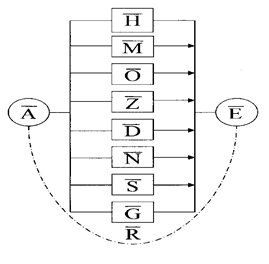
Рисунок 11.6 – Схема расчёта надёжности БСН по критерию отказа.
Начальный и конечные узлы сети обозначены здесь соответственно через  и
и 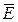 . Поскольку система неработоспособна, если отказал хотя бы один элемент, то начальные и конечные узлы всех ребер должны совпадать соответственно с начальным узлом системы
. Поскольку система неработоспособна, если отказал хотя бы один элемент, то начальные и конечные узлы всех ребер должны совпадать соответственно с начальным узлом системы  и с ее конечным узлом
и с ее конечным узлом 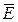 , поэтому все события на рисунке…… представлены параллельно включенными элементами.
, поэтому все события на рисунке…… представлены параллельно включенными элементами.
При построении дерева отказов исходят из отказа системы («вершинное событие») и сводят это событие к отказам элементов («базисные события»).
Логические связи между базисными событиями, которые порождают вершинное событие, отражаются в направленном графе, имеющем древовидную структуру. Дерево отказов для примера с БСН показано на рисунке 11.7.
Рисунок 11.7 - Дерево отказов.
Базисные события 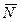 ,
,  ,
, 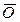 ,….,
,…., 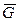 связаны между собой логическими звеньями ИЛИ (знак V). Менее употребительным является построение так называемых деревьев работоспособности. Для примера с БСН дерево работоспособности имеет вид, изображенный на рисунке 11.8. События N, M, Oсоединены логическими звеньями И (знак Ù).
связаны между собой логическими звеньями ИЛИ (знак V). Менее употребительным является построение так называемых деревьев работоспособности. Для примера с БСН дерево работоспособности имеет вид, изображенный на рисунке 11.8. События N, M, Oсоединены логическими звеньями И (знак Ù).

Рисунок 11.8 - Дерево работоспособности.
Параллельной системой называется такая система, которая работоспособна, если работоспособен хотя бы один из ее элементов; она отказывает тогда и только тогда, когда отказывают все ее элементы.
Параллельные системы также часто встречаются в реальных технических системах. Для нее расчетная схема надёжности по критерию работоспособности изображается в виде параллельного включения элементов, обозначающих соответствующие события.
Пусть событие, состоящее в том, что v – Й элемент работоспособен, обозначается через Xv, v =1,...,п. Событие, состоящее в работоспособности системы, обозначим через S, а состояния отказа помечаются чертой сверху.
Тогда для параллельной системы имеем четыре формы графического представления, изображенные на рисунке 11.9.

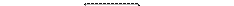


 | |||
 | |||


Рисунок 11.9 – Различные формы графического представления схем расчета надёжности для параллельной системы.
Часто оказывается, что исследуемая техническая система не является чисто параллельной или последовательной, а представляет собой синтез этих двух типов, т.е. является комбинированной системой (Рисунок 11.10).

Рисунок 11.10 – Пример комбинированной системы(синтез параллельной и последовательной систем).
Одни и те же расчетные схемы надёжности могут получаться для совершенно различных объектов. Например, элементы 1, 2, 3, 4, 5 на рисунке 11.11 могут означать электрические соединения.
В зависимости от задачи исследования на практике отдается предпочтение тому или иному из четырех способов представления расчетных схем надёжности:
- расчетной схеме по критерию работоспособности;
- расчетной схеме по критерию отказа;
- дереву отказов;
- дереву работоспособности.
Однако принципиально они аналогичны и могут быть сведены одна к другой. Если сравнить модели надёжности, имеющие вид двухполюсных сетей, с моделями, имеющими вид деревьев, то видна тесная связь между деревьями отказов и расчетными схемами надёжности по критерию отказа, с одной стороны, и деревьями работоспособности – с другой.
При формировании дерева отказов исходят из определенного нежелаемого вершинного события и анализируют возможные причины его возникновения. При этом, естественно, стремятся к разумной степени детализации. Готовое дерево отказов представляет в виде логической диаграммы все последовательности событий, которые могут привести к основному событию.
С помощью метода деревьев отказов получают:
- систематизированное представление всех возможных причин вершинного события (отказа системы) и их взаимодействие;
- обозримый и доступный для изучения материал анализа причин отказа;
- параметры надёжности системы, полученные в результате количественного анализа деревьев.
Построение дерева отказов предполагает детальный анализ процесса функционирования системы.
Одному и тому же вершинному событию, как правило, можно поставить в соответствие несколько различных деревьев отказов. Прежде чем начать построение дерева отказов, нужно выполнить следующие предварительные действия:
- проанализировать (при необходимости – составить) детальное описание рабочего процесса рассматриваемой системы, включая анализ подсистем(схемы, описания конструкции и т.д.), в том числе всех значимых параметров элементов;
- проанализировать физические и химические свойства материалов, используемых в устройствах, связанных или соседствующих с рассматриваемой системой;
- проанализировать характеристики безотказности, которые для элементов исследуемой системы должны быть известны;
- использовать соответствующую удобную символику обозначений.
Исходным моментом построения дерева отказов является установление вершинного события для исследуемой системы. Далее рассматриваются возможности представления вершинного события как отказ одного из элементов системы. Если это возможно, то такое событие соединяется звеном ИЛИ с тремя входами - «первичный отказ», «вторичный отказ», и «эксплуатационный отказ». Если это не так, то пытаются свести вершинное событие к таким отказам, которые сами по себе или совместно порождают основное событие.
Необходимо следить, чтобы список причин был полным, так как упущение возможных событий, приводящих к отказам, является основной причиной погрешностей при построении деревьев отказов.
Установленные события - отказы, как и вершинное событие, подвергаются дальнейшей детализации. Из каждого такого события развивается «ветвь дерева». Общая схема построения дерева отказов представлена на рисунке 11.11.
Структурные функции сложных систем
Ранее нами отмечалось, что в СС имеются два вида зависимостей:
- между элементами системы;
- зависимость элемент – система.
При выборе структурных функций (математических моделей структур) преобладающей является зависимость элемент – система.
Для обозначения i-го элемента системы принимаем булевы переменные:
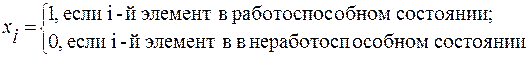 .
.
При этом состояние системы, имеющей nэлементов, можно характеризовать n-мерным вектором 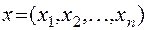 .
.
Множество возможных состояний системы будет равным 2n. В зависимости от конкретной структуры системы все это множество состоит из двух подмножеств, соответствующих состояниям работоспособности и неработоспособности системы. Тогда на множестве 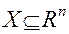 представляется целесообразным задать определенную булеву функцию
представляется целесообразным задать определенную булеву функцию 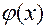 , которая называется структурной функцией:
, которая называется структурной функцией:
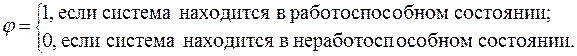
Предполагая далее, что состояние системы полностью определяется состоянием ее элементов, можно записать как (11/25):
 , (11/25)
, (11/25)
где x = (x1,……,xn).

Рисунок … - Общая схема построения дерева отказов
Рисунок 11.11 - Общая схема построения дерева отказов.
Рассмотрим несколько простейших структур системы и соответствующих булевых функций.
Последовательная структура системы – структура, при которой отказ хотя бы одного элемента системы приводит к ее отказу. Это свойство системы представляется с помощью формулы структурной функцией последовательной системы 11.26:
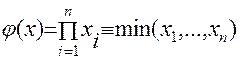 (11.26)
(11.26)
Графическое представление структуры приведено на рисунке 11.12.
1 2 n

Рисунок 11.12 – Последовательное соединение элементов
Система с параллельной структурой (Рисунок 11.13) работоспособна тогда, когда работоспособен хотя бы один из ее элементов. Структурная функция в этом случае:
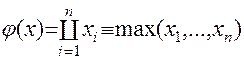 , (11.27)
, (11.27)
где  .
.
Дополнительно вводится обозначение: 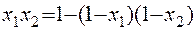 .
.

Рисунок 11.13 – Параллельное соединение элементов.
Структура системы, при которой она работоспособна только тогда, когда не менее k из n элементов работоспособны, называют структурой типа «kиз n». Структурная функция такой системы представляется в виде системы (11.28):
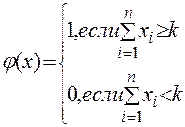 . (11.28)
. (11.28)
Необходимо заметить, что параллельная и последовательная структуры являются частными случаями структуры «kизn», поскольку структура «nизn», есть последовательная, а «1изn» - параллельная.
Иллюстрацией структуры «2 из 3» может служить рисунок 11.14. Структурная функция имеет в этом случае вид:
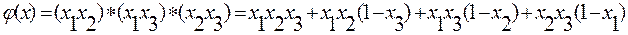
Эту систему в теории надёжности называют последовательно-параллельной.

Рисунок 11.14 – Структура типа «2 из 3».
Более распространенный другой тип смешанного соединения элементов – параллельно-последовательная структура (Рисунок 11.15), структурная функция которой представляется в виде (11.29):
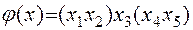 . (11.29)
. (11.29)

Рисунок 11.15 - Параллельно-последовательная структура
Сложные структуры, которые могут быть упрощены путем сведения к простейшей двухполюсной схеме (одному элементу), называются системами с приводимой структурой (Рисунок 11.16).

Рисунок 11.16 – Схема трансформации системы с приводимой структурой.
Система с неприводимой структурой (Рисунок 11.17) таких преобразований не допускает, поэтому структурный анализ таких систем является более сложным.

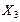
Рисунок 11.17 – Система с неприводимой структурой.
Представление состояния системы через бинарную функцию 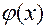 , а элементов через булевы переменные
, а элементов через булевы переменные  позволяет значительно упростить процедуру расчета безотказности за счет использования свойств поглощения логических переменных.
позволяет значительно упростить процедуру расчета безотказности за счет использования свойств поглощения логических переменных.
В этом случае математическое ожидание случайной величины:
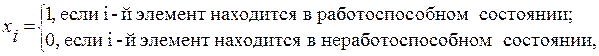
есть 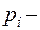 показатель безотказности i-го элемента в произвольный момент времени, т.е.
показатель безотказности i-го элемента в произвольный момент времени, т.е. 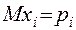 .
.
В случае независимости элементов 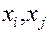 и
и 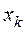 :
:
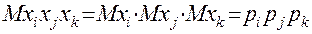 (11.30)
(11.30)
Аналогичным образом определяется показатель надёжности системы:
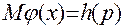 , (11.31)
, (11.31)
где 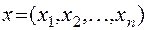 и
и  .
.
Для определения вероятности безотказной работы с последовательной структурой в произвольный момент времени:
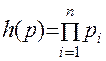 (11.32)
(11.32)
Для системы с параллельной структурой:
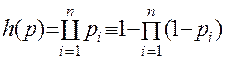 (11.33)
(11.33)
Для структуры «2 из 3»:
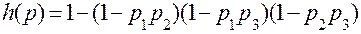 (11.34)
(11.34)
В предположении 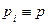 система «kизn» имеет функцию надёжности (11.35):
система «kизn» имеет функцию надёжности (11.35):
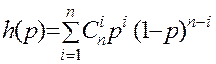 , (11.35)
, (11.35)
где 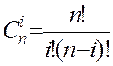 - число сочетаний из n элементов по i.
- число сочетаний из n элементов по i.
Нижняя и верхняя оценки вероятности безотказной работы системы:
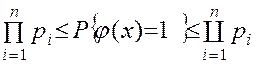 (11.36)
(11.36)
Здесь 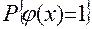 - оператор математического ожидания, примененный к выражению (11.37):
- оператор математического ожидания, примененный к выражению (11.37):
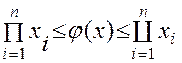 (11.37)
(11.37)
поскольку характеристики любой приводимой системы снизу характеристиками системы с последовательной структурой, а сверху характеристиками системы с параллельной структурой.
Резервирование в сложных системах
Среди постоянных инженерных проблем – создание систем с высокими показателями надёжности из ненадёжных элементов путем соответствующей организации избыточности.
Известно, что монотонная избыточная система, состоящая из независимых элементов, имеет S-образную зависимость между ее безотказностью и безотказностью ее наихудшего элемента p (Рисунок 11.18 ).

Рисунок 11.18 – S – образная функция.
Существует такой уровень безотказности 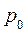 наихудшего элемента системы, при котором безотказность всей системы
наихудшего элемента системы, при котором безотказность всей системы 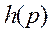 оказывается выше
оказывается выше 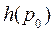 , то есть
, то есть 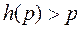 , при
, при 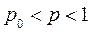 .
.
Для любой такой системы функция 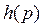 пересекает диагональ (функцию
пересекает диагональ (функцию 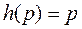 ) один раз при
) один раз при 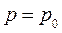 .
.
Изложенное является логическим обоснованием способа создания избыточности систем – резервирования, изложенного ниже.
При создании и в процессе эксплуатации систем широко распространен способ повышения их безотказности за счет введения в их конструкции дополнительных элементов, которые могут работать параллельно с основными элементами или подключаться на место отказавшего элемента. Таким образом, резервированной системой называется такая система, в которой отказ наступает только после отказа любого основного элемента и всех его резервных элементов.
Классификация способов резервирования показаны на рисунке 11.19.

Рисунок 11.19 – Способы резервирования.
При общем резервировании основной объект (система) резервируется в целом, а при раздельном – резервируются отдельные части (элементы) системы. Под кратностью резервирования «m» понимается отношение числа резервных элементов к числу основных.
При резервировании с целой кратностью величина m есть целое число (например, если m = 2, то на один основной элемент приходится два резервных). При резервировании с дробной кратностью показателем является дробное несокращаемое число. Например, при m=4/2, резервных элементов 4, основных 2, общее число элементов 6. Сокращать дробь нельзя, так как новое отношение может отражать другой конструктивный или физический смысл.
По способу включения резервирование разделяется на постоянное и резервирование замещением. При постоянном резервировании резервные элементы подключены к нагрузке постоянно в течение всего времени работы и находятся в одинаковых с основными элементами условиях. При резервировании замещением элементы, замещающие основные, подключаются к нагрузке после отказа основных элементов.
Резервирование замещением может быть нагруженным, облегченным и ненагруженным. Достоинством резервирования замещением с ненагруженным резервом является то, что работоспособность резервных элементов сохраняется более длительное время, так как до момента включения они находятся в нерабочем состоянии.
Достоинством постоянного резервирования является его простота, так как в этом случае не требуется никаких переключающих устройств и устройств, отслеживающих процесс снижения работоспособности и сигнализирующих о наступлении отказа.
Систему с общим резервированием с постоянно включенным резервом с целой кратностью отражает схема, изображенная на рисунке 11.20. Здесь параллельно основной цепи включено «m» резервных цепей, имеющих такие же параметры элементов, как и в основной цепи.

Рисунок 11.20 – Схема с общим нагруженным резервированием (количество резервных цепей 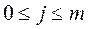 ).
).
Анализ приведенной схемы резервирования выполним при следующих допущениях:
отказы элементов являются случайными и независимыми событиями;
переключающие устройства идеальны (их безотказность P(t)=1, а основная и резервные цепи равнонадёжны);
ремонт резервированной системы исключен.
Исходя из принятых допущений для основной и резервных цепей, определим вероятность безотказной работы по формуле (11.38):
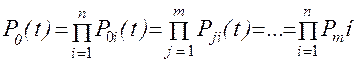 , (11.38)
, (11.38)
где 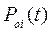 - вероятность безотказной работы i-го элемента основной «0» цепи;
- вероятность безотказной работы i-го элемента основной «0» цепи;
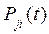 - вероятность безотказной работы i-го элемента j-ой цепи.
- вероятность безотказной работы i-го элемента j-ой цепи.
Поскольку все одноименные элементы в каждой цепи имеют одинаковые параметры и находятся в одинаковых условиях, то их безотказность в одно и тоже время t одинакова. Следовательно, для всей цепи:
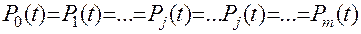 (11.39)
(11.39)
Соответственно вероятность отказов анализируемых цепей:
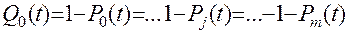 (11.40)
(11.40)
отказ системы наступит, если откажет основная цепь и все резервные. Математически это состояние отражается зависимостью:
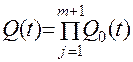 , (11.41)
, (11.41)
где 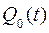 - вероятность отказа основной цепи.
- вероятность отказа основной цепи.
Поскольку все цепи идентичны и находятся в одинаковых условиях, то 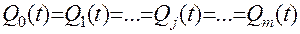 , а вероятность отказа системы рассчитывается по формуле (11.42):
, а вероятность отказа системы рассчитывается по формуле (11.42):
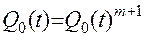 (11.42)
(11.42)
Используя зависимость (11.43), запишем:
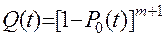 (11.43)
(11.43)
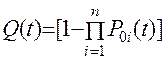 (11.44)
(11.44)
Резервированная система может находиться в одном из двух полярных состояний – работоспособном, когда хотя бы одна из цепей работоспособна, и неработоспособном, когда отказали все m+1 цепи, т.е. 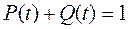 .
.
В результате получаем, что вероятность безотказной работы системы с количеством цепей m+1 равна (11.45):
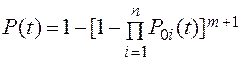 (11.45)
(11.45)
В случае простейшего потока отказов в каждой из цепей ( 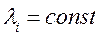 ):
):
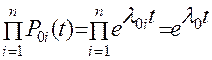 (11.46)
(11.46)
Здесь 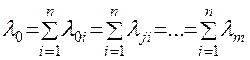
Тогда вместо выражения (11.46) запишем в виде (11.47):
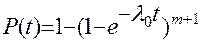 , (11.47)
, (11.47)
где 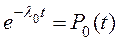 - вероятность безотказной работы основной цепи.
- вероятность безотказной работы основной цепи.
Средняя наработка до отказа резервированной системы:
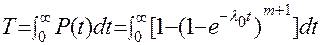 (11.48)
(11.48)
Выполнив преобразования, получим:
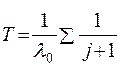 ;
; 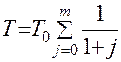 (11.49)
(11.49)
Интенсивность отказов системы определяется по зависимости (11.50):
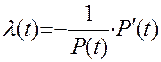 (11.50)
(11.50)
Для более наглядного представления выигрыша по критерию безотказности системы при использовании общего нагруженного резервирования с целой кратностью построим график зависимости 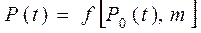 (Рисунок 11.21).
(Рисунок 11.21).
Из рисунка 11.21 видно, что, если 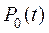 имеет малое значение, например,
имеет малое значение, например, 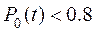 , то и при m>2 просматривается существенное приращение безотказности.
, то и при m>2 просматривается существенное приращение безотказности.

Рисунок 11.21 – Повышение вероятности безотказной работы системы при включении m резервных цепей.
Однако, с увеличением безотказности основной цепи 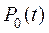 , эффективность применения нескольких резервных ветвей снижается. Если безотказность основной цепи
, эффективность применения нескольких резервных ветвей снижается. Если безотказность основной цепи 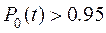 , то заметен существенный прирост
, то заметен существенный прирост 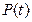 при включении только одной резервной цепи.
при включении только одной резервной цепи.
Способ нагруженного дублирования (Рисунок 11.22) является частным случаем общего нагруженного резервирования с целой кратностью, m=1, то есть на одну основную цепь приходится одна резервная цепь, находящаяся под нагрузкой.

Рисунок 11.22 – Расчетная схема нагруженного дублирования (l0 =l1=const).
Используя зависимость (11.46), определим вероятность безотказной работы системы по формуле (11.51):
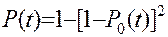 , (11.51)
, (11.51)
где 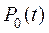 - вероятность безотказной работы основной цепи (
- вероятность безотказной работы основной цепи ( 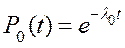 ).
).
Используя зависимость (11.47), определим среднюю наработку до отказа системы по формуле (11.52):
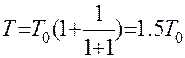 (11.52)
(11.52)
Подставив в выражение (11.47) исходное выражение (11.51) и его производную, получим выражение (11.53):
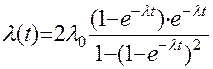 (11.53)
(11.53)
Для построения графика 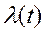 (Рисунок 11.23) определим предельные значения этой функции:
(Рисунок 11.23) определим предельные значения этой функции:
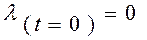 ;
;
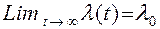 .
.


Рисунок 11.23 - Интенсивность отказов системы, работающей в режиме нагруженного дублирования
Из рисунка 11.23 видно, что интенсивность отказов системы со временем возрастает. Это говорит о том, что при большом t вероятность отказа одной из цепей высока, и система может перейти в режим работы с одним элементом 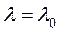 . Отметим также начальный этап, на котором система имеет очень высокий уровень безотказности.
. Отметим также начальный этап, на котором система имеет очень высокий уровень безотказности.
На рисунке 11.24 представлен график функции P(t), построенный по зависимости (11.50). Здесь также приведен график 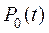 основной цепи (без резерва).
основной цепи (без резерва).


Рисунок 11.24 – Зависимость вероятностей безотказной работы основной цепи P(t) исистемы из двух элементовP(t) отl0t.
На рисунке 11.24 видна степень повышения безотказности системы, переведенной в режим нагруженного дублирования.
При резервировании замещениемрезервные элементы включаются только при отказе основных.
Предположим, что приборы, обнаруживающие отказ основной цепи, и выключатели, отключающие оставшуюся цепь и включающие резервную, также абсолютно надёжны. Резервная ненагруженная цепь, находящаяся в режиме ожидания, своих характеристик не изменяет и работоспособна. Каждая из цепей состоит из n последовательных элементов (Рисунок 11.25).

Рисунок 11.25 - Схема системы дублирования замещением
Учитывая что 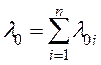 ;
;  ;
; 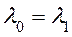 , анализируемая система (схема) приобретает вид, изображенный на рисунке 11.26.
, анализируемая система (схема) приобретает вид, изображенный на рисунке 11.26.

Рисунок 11.26 – Расчетная схема при дублировании замещением.
Проанализируем возможные гипотезы, адекватные событиям, которые могут произойти с системой на отрезке времени t.
Основная цепь отработала безотказно все время t, и резервную цепь включать не требовалось. Вероятность этого для системы - 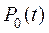 .
.
Основная цепь отработала только отрезок 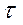 и отказала. При этом сразу же включилась резервная цепь и успешно проработала до конца времени t с вероятностью безотказной работы
и отказала. При этом сразу же включилась резервная цепь и успешно проработала до конца времени t с вероятностью безотказной работы 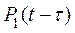 .
.
Чтобы работал второй режим, необходимо совпадение двух событий – отказ основной цепи и безотказная работа включенной под нагрузку резервной цепи. Математической оценкой совпадения этих событий является произведение их вероятностей. На рисунке 11.27 изображен график плотности вероятности появления отказа основной цепи 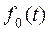 .
.
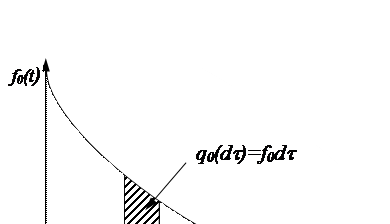
Рисунок 11.27 - График функции l(t) системы, дублированной замещением
Выделим малый интервал 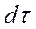 , следующий за отрезком
, следующий за отрезком 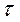 . Произведение
. Произведение 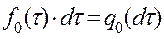 . Заштрихованная площадка, численно равна вероятности отказа основной цепи на интервале
. Заштрихованная площадка, численно равна вероятности отказа основной цепи на интервале 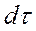 . Выражение
. Выражение 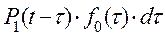 представляет собой математическую оценку факта отказа основной цепи и успешного вхождения в работу резервной цепи в момент
представляет собой математическую оценку факта отказа основной цепи и успешного вхождения в работу резервной цепи в момент 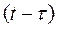 .
.
Вероятность безотказной работы анализ
Дата добавления: 2015-01-13; просмотров: 1901;
