Рассмотрим простой экспрессный метод количественного анализа риска
Величина риска, как мы уже определили ранее, определяется совокупностью вероятности неблагоприятного события и его последствиями – потерями или ущербом. Таким образом, можно записать следующее выражение для количественного определения риска:
R=C∙p, где: C - величина потерь, p - вероятность события, приводящего к таким потерям. При этом мы имеем в виду некоторое среднее значение потенциального риска. Реально реализующийся риск может оказаться любым – от нулевого до максимального.
Если к потерям разного масштаба могут привести несколько неблагоприятных событий, реализующихся с разной вероятностью, суммарный средний потенциальный риск равен:
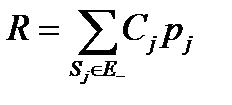 .
.
В этом выражении Е- - подмножество неблагоприятных событий или состояний. Вероятности pj могут зависеть от времени t. В технических устройствах возможны так. называемые обратные переходы – переходы из неблагоприятных состояний в благоприятные, образующие подмножество Е+. Такие переходы имеют место в результате ремонта или восстановления технического устройства. С учетом сказанного выражение для риска существенно усложняется:
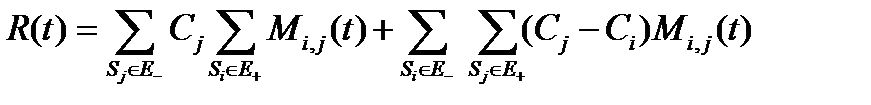 .
.
Здесь первый множитель первого слагаемого отражает переходы в неблагоприятные состояния, а второй – обратные переходы в благоприятные состояния, второе слагаемое характеризует возможные переходы из одних неблагоприятных состояний в другие неблагоприятные состояния. Mi,j – число переходов из всех состояний i в состояние j. Если таких переходов нет, то второе слагаемое равно нулю.
Возрастающий со временем риск называют кумулятивным риском. Рассмотрим оценку риска на примере.
ПРИМЕР 40
Нерезервированная неремонтируемая система состоит из 4-х элементов, для которых известны интенсивности отказов λi и величины ущерба при отказах ri:
| i | λi , ч-1 | ri , усл. ед. |
| 3∙10-5 | ||
| 5∙10-4 | ||
| 7∙10-5 | ||
| 2∙10-7 |
Требуется оценить средний потенциальный риск для случая его экспоненциального распределения.
Для последовательной ССН находим: 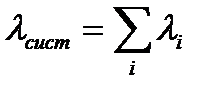 =6∙10-4ч-1.
=6∙10-4ч-1.
При экспоненциальном распределении риска:
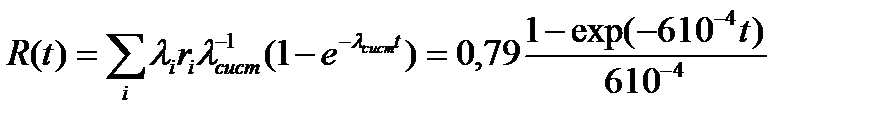 .
.
Интересно отметить, что при таком методе оценки риска кумулятивный риск системы с восстановлением, у которой показатель надежности выше, чем у системы без восстановления, оказывается выше риска последней. Это иллюстрирует рис. 26.
| Рис. 26. Кумулятивный риск систем с (1) и без (2) восстановления |
| λt |
| R(t) |
Для описания связи величины риска с частотой соответствующего этому риску неблагоприятного события используют гиперболический закон Парето:
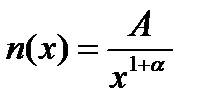 ,
,
где: n(x) – число элементов, встречающихся х раз в данной совокупности;
А, α – коэффициенты распределения.
Подобными гиперболическими законами описывается, например, распределение богатства в обществе, количества жителей в городах и др.
Применительно к риску, гиперболический закон записывают в более удобных формах:
R=ax-b, или lnR=lna - b∙lnx,
где: R – риск (ущерб), x – частота (число) событий.
Иллюстрация применения гиперболического закона при установлении предельного уровня вредных (радиационных) воздействий (рис. 27 по В. Скулкину).
| Область приемлемого риска |
| Область недопустимого риска |
| ПДВ 0,05 мЗв/год |
| ПДВ 5 мЗв/год |
| 10-5 10-3 10-1 101 отказы в год |
| мЗв в год 101 100 10-1 10-2 |
| Рис. 27. Предельные уровни радиационных воздействий ЯЭУ |
Аналогичный подход, основанный на рисках, применяется при оценке функциональной безопасности (ФБ) программных средств (ПС) и программируемых электронных компонент (ПЭК). Ключевыми документами в этой сфере являются стандарты МЭК серии 61508: IEC 61508 Functional safety: safety related systems – 7 pats, 1999.
Примеры оценивания риска приведены в ЛР 6 и ПЗ 9.
Дата добавления: 2015-03-19; просмотров: 1059;
