Моделирование электрических нагрузок
Статические характеристики для каждого типа электрической нагрузки и их совокупностей могут быть получены экспериментально. Однако в каждом конкретном случае это затруднительно и чаще всего пользуются так называемыми типовыми характеристиками. Так, например, можно выделить статические характеристики асинхронных двигателей малой, средней и большой мощности или статические характеристики определенного состава смешанной нагрузки. Полученные по таким нагрузкам статические характеристики обобщаются и представляются в виде математических моделей. В общем случае статические характеристики нагрузки по напряжению могут быть представлены в виде
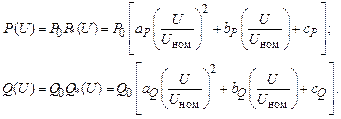
где P0 и Q0 – активная и реактивная мощности нагрузки при номинальном напряжении; P*(U) и Q*(U) – статические характеристики нагрузок в относительных единицах; Uном – номинальное напряжение нагрузки или сети; aP, aQ, bP, bQ, cP и cQ – коэффициенты (параметры) моделей, полученные в результате обработки экспериментальных данных.
Средние статические характеристики примерно соответствуют следующему составу нагрузки, %:
Крупные асинхронные двигатели..................................................... 15
Мелкие асинхронные двигатели........................................................ 35
Крупные синхронные двигатели....................................................... 9
Печи и ртутные выпрямители............................................................. 11
Освещение и бытовая нагрузка.......................................................... 22
Потери в сетях......................................................................................... 8
Обычно принимается aP = 0, т. е. линейная зависимость активной нагрузки от напряжения. Коэффициенты bP и cP в зависимости от характеристики узла нагрузки приведены в табл. 2.4.
Таблица 2.4
Значения коэффициентов bP и cP
| Характер нагрузки | Статические характеристики | |||||
| пологие | средние | крутые | ||||
| bP | cP | bP | cP | bP | cP | |
| Преобладают крупные промышленные предприятия | 0,3 | 0,7 | 0,6 | 0,4 | 0,9 | 0,1 |
| В среднем | 0,4 | 0,6 | 0,9 | 0,1 | 1,4 | –0,4 |
| Крупных промышленных предприятий нет | 0,9 | 0,1 | 1,2 | –0,2 | 1,5 | –0,5 |
Коэффициенты aQ, bQ и cQ в зависимости от коэффициента мощности приведены в табл. 2.5.
Таблица 2.5
Значения коэффициентов aQ, bQ и cQ
| Коэффициент мощности | Статические характеристики | ||||||||
| пологие | средние | крутые | |||||||
| aQ | bQ | cQ | aQ | bQ | cQ | aQ | bQ | cQ | |
| 0,83…0,87 | –18 | 9,6 | –15,3 | 6,7 | –14,4 | 5,4 | |||
| 0,88…0,90 | 11,9 | –21,8 | 10,9 | 11,4 | –18,5 | 8,1 | 11,9 | –17,4 | 6,5 |
| 0,91…0,93 | 14,1 | –26,2 | 13,1 | 13,5 | –22,2 | 9,7 | 14,1 | –21 | 7,9 |
Моделирование электрических нагрузок статическими характеристиками по напряжению в расчетах установившихся режимов считается наиболее точным способом учета потребляемой мощности нагрузки. Однако для получения действительных статических характеристик требуются экспериментальные исследования, а для подбора типовых статических характеристик должен быть известен состав нагрузки, который может сильно изменяться во времени. Кроме того, в этом случае в расчетах непременно следует учитывать действие регуляторов напряжения, что значительно усложняет подготовку данных и требует знания законов регулирования.
Поэтому в большинстве случаев пользуются самой простой моделью нагрузки – постоянными значениями активной и реактивной мощности: P = const, Q = const.
В некоторых задачах, в которых выполняются расчеты установившихся режимов, токов короткого замыкания в электрической сети или расчеты устойчивости ЭЭС, нагрузки принято представлять схемами замещения. Такое представление является точным в том случае, если для нагрузки известны ее статические характеристики и величина подведенного напряжения. В других случаях такие модели являются приближенными.
Рассмотрим электрическую цепь, в которой имеется нагрузка, представленная в виде сопротивления Zн. Это сопротивление в общем случае является переменной величиной – получается нелинейная электрическая цепь. Даже если считать мощность, потребляемую нагрузкой, постоянной, сопротивление будет меняться в зависимости от напряжения по формуле
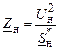 . (2.53)
. (2.53)
Кроме того, мощность также зависит от напряжения по статической характеристике и поэтому
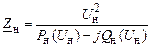 . (2.54)
. (2.54)
Нагрузка может быть представлена в виде двух схем замещения: с последовательным и параллельным соединением элементов (рис. 2.18).
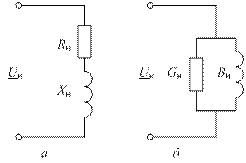
Рис. 2.18. Схемы замещения нагрузки
При последовательном соединении:
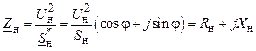 , (2.55)
, (2.55)
а при параллельном:
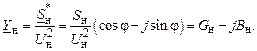 (2.56)
(2.56)
При постоянной величине заданного сопротивления или проводимости моделирование с помощью выражений (2.55) и (2.56) дает характеристики:
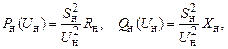
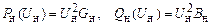 . (2.57)
. (2.57)
Моделирование постоянным сопротивлением дает обратную квад-ратичную зависимость от напряжения, а постоянной проводимостью – зависимость пропорционально квадрату напряжения. Вторая модель хорошо согласуется с моделью статической характеристики реактивной мощности нагрузки (2.52), поэтому для реактивной мощности вполне приемлема. Для активной мощности можно, например, воспользоваться линейной моделью, тогда будем иметь:
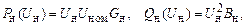 (2.58)
(2.58)
где Gн и Bн вычислены при номинальном напряжении нагрузки.
На рис. 2.19 представлены действительные статические характеристики нагрузки (сплошные линии) и характеристики, полученные по моделям (2.58) – пунктирные линии.
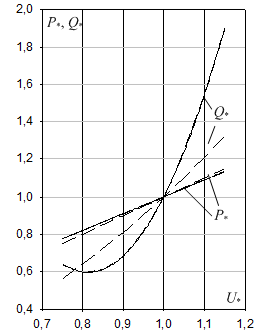
Рис. 2.19. Действительные статические характеристики нагрузки и зависимости мощностей от напряжения при модели-
ровании нагрузки схемой замещения
Иногда в качестве данных по нагрузке бывают известны измеренные токи нагрузки. Принимая какое-либо значение коэффициента мощности нагрузки, ее можно моделировать постоянными значениями токов Iн:
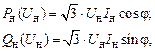 (2.59)
(2.59)
что дает линейные статические характеристики как активной, так и реактивной мощности. Такие модели нагрузки используются в низковольтных сетях и сетях среднего напряжения.
Все математические модели электрических нагрузок, рассмотренные выше, сведены в табл. 2.6.
Таблица 2.6
Математические модели электрических нагрузок
| Математические модели | Мощность нагрузки | Примечания |
| Статические характеристики нагрузки по напряжению | 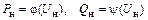
| Получаются по данным эксперимента или подбором типовых характеристик |
| Постоянные значения мощности нагрузки | 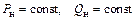
| |
| Схема замещения: Yн = Gн – jBн = = const | 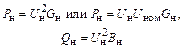
| 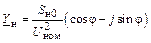
|
| Схема замещения: Zн = Rн + jXн = = const | 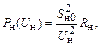
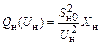
| 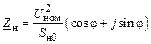
|
| Постоянное значение тока нагрузки: Iн = const (φ = const) | 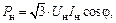
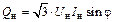
| 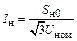
|
Примечание. Во всех формулах Sн0 – полная мощность нагрузки, которая может быть принята равной номинальной или максимальной мощности, а также мощности некоторого исходного или начального режима работы электроприемника или потребителя.
Пример.Найти коэффициенты статической характеристики нагрузки по опытным данным для активной и реактивной мощности и определить их регулирующие эффекты.
Используем линейную модель для активной мощности и параболу для реактивной мощности. Построение характеристик выполним в Mathcad.
Все величины приведены в относительных единицах.
Исходные данные (результаты эксперимента):
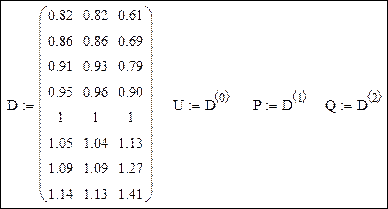
Коэффициенты функции полиномиальной регрессии:
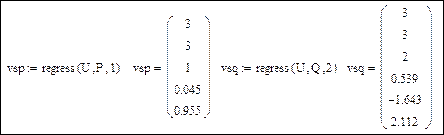
Определение функций статических характеристик и аргументов:
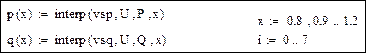
Графики статических характеристик (на графике отдельными маркерами нанесены экспериментальные данные):
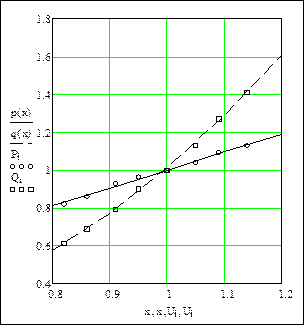
Регулирующие эффекты:
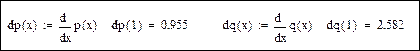
Изменение регулирующих эффектов:
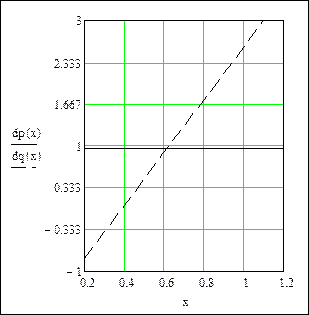
Регулирующий эффект активной мощности не меняется, так как модель статической характеристики была принята линейной.
Дата добавления: 2015-03-19; просмотров: 5851;
