Задачи о положениях манипуляторов.
Первый вопрос, с которым сталкивается создатель манипулятора, - выбор его кинематической схемы, структуры его скелета. В процессе выполнения операций с объектами манипулирования в большинстве случаев манипуляторы имитируют движение рук человека. Поэтому структурная схема манипулятора должна обладать кинематическими характеристиками, аналогичными характеристикам руки человека. Подвижности, имеющиеся у руки человека (без 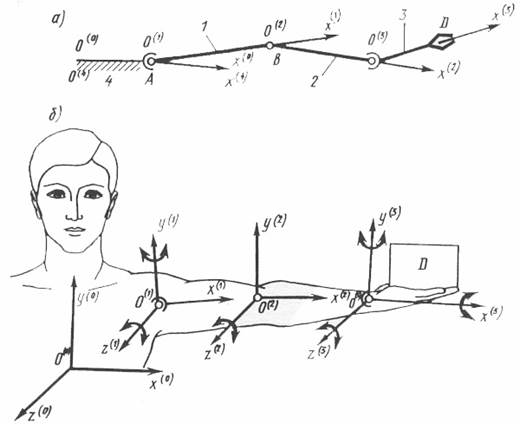 учета подвижностей пальцев), можно обеспечить с помощью пространственной кинематической цепи, у которой к неподвижному звену 4 (аналог лопатка) посредством различных кинематических, пар присоединяются звенья (рис. 24.2) трехподвижной парой А - звено 1 (плечо), через одноподвижную пару В - звено 2 (предплечье) - и трехподвижной парой 3 (кисть). Используя для оценки степени подвижности руки человека формулу Малышева без учета движения кисти (пальцев и фаланг), получим W = l ; с учетом всех звеньев и в самой кисти имеем W = 27.
учета подвижностей пальцев), можно обеспечить с помощью пространственной кинематической цепи, у которой к неподвижному звену 4 (аналог лопатка) посредством различных кинематических, пар присоединяются звенья (рис. 24.2) трехподвижной парой А - звено 1 (плечо), через одноподвижную пару В - звено 2 (предплечье) - и трехподвижной парой 3 (кисть). Используя для оценки степени подвижности руки человека формулу Малышева без учета движения кисти (пальцев и фаланг), получим W = l ; с учетом всех звеньев и в самой кисти имеем W = 27.
|
|
|
 Каждая степень подвижности манипуляционного робота управляется индивидуальным приводом, в результате чего исполнительный орган получает направленное вполне определенное движение. В современных манипуляторах используют электромеханические, гидравлические, пневматические или комбинированные приводы.
Каждая степень подвижности манипуляционного робота управляется индивидуальным приводом, в результате чего исполнительный орган получает направленное вполне определенное движение. В современных манипуляторах используют электромеханические, гидравлические, пневматические или комбинированные приводы.
|
Глобальные движения осуществляются путем перемещения подвижного основания робота с помощью двигательной системы. В стационарных роботах глобальные движения отсутствуют. Их станины неподвижно крепятся к полу, кронштейну или потолку возле технологического оборудования.
 Региональные движения - перемещения схвата робота в различные зоны рабочего пространства, определяемого размерами звеньев манипулятора.
Региональные движения - перемещения схвата робота в различные зоны рабочего пространства, определяемого размерами звеньев манипулятора.
|
 Иногда глобальные и региональные движения называют транспортирующими движениями, а локальные - ориентирующими.
Иногда глобальные и региональные движения называют транспортирующими движениями, а локальные - ориентирующими.
|
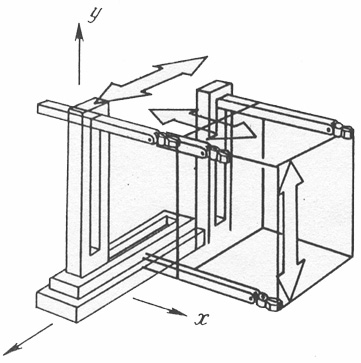
манипулятор (рис. 24.3), функционирующий в декартовой (прямоугольной) системе координат, прост в управлении и отличается высокой точностью действий. Схват манипулятора поступательно перемещается вдоль трех основных осей: х, у и z (т. е. слева направо, вперед-назад и вверх-вниз);
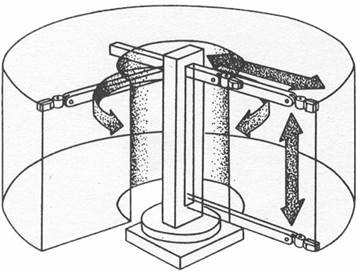
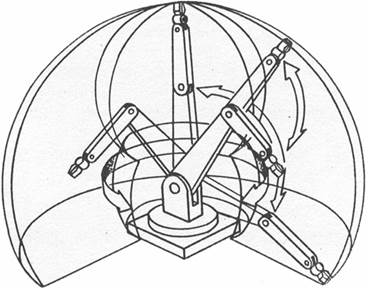 манипулятор (рис. 24.4), работающий в цилиндрической системе координат. Его схват может выдвигаться и втягиваться, а также перемещаться вверх и вниз вдоль стойки. Кроме того, весь узел манипулятора может поворачиваться вокруг оси основания, но не на полный оборот, что позволяет ему выполнять операции в окружающей цилиндрической зоне;
манипулятор (рис. 24.4), работающий в цилиндрической системе координат. Его схват может выдвигаться и втягиваться, а также перемещаться вверх и вниз вдоль стойки. Кроме того, весь узел манипулятора может поворачиваться вокруг оси основания, но не на полный оборот, что позволяет ему выполнять операции в окружающей цилиндрической зоне;
|
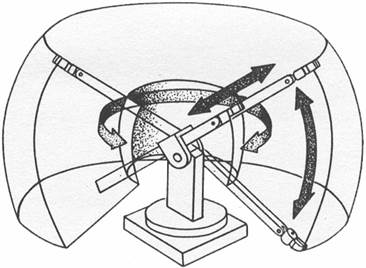
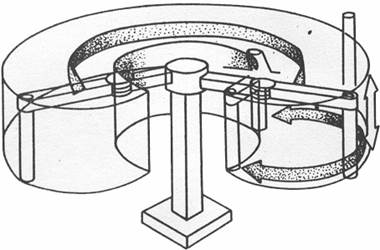 перемещения манипулятора достигаются путем поворота его в вертикальной плоскости в «плечевом» суставе. Весь узел манипулятора может также поворачиваться вокруг оси
перемещения манипулятора достигаются путем поворота его в вертикальной плоскости в «плечевом» суставе. Весь узел манипулятора может также поворачиваться вокруг оси
|
шарнирный манипулятор (рис.24.6), действующий в ангулярной системе координат, не имеет поступательных кинематических пар, а имеет только вращательные кинематические пары. Манипулятор такого типа очень напоминает руку человека, поскольку имеет «плечевое» и «локтевое» сочленения, а также «запястье». Его зона обслуживания значительно больше, чем у роботов других типов. Он способен обходить препятствия гораздо более разнообразными путями и даже складываться, но вместе с тем он исключительно сложен в управлении;
своеобразную схему имеет манипулятор системы SCARA (рис. 24.7), представляющий собой вариант манипулятора с цилиндрической системой координат. Все кинематические пары этого манипулятора располагаются в горизонтальной плоскости, благодаря чему механизм способен разворачиваться подобно складной ширме. Его зона обслуживания имеет цилиндрическую форму.
Перспективными представляются роботы еще двух типов. Первый из них, «Spine» (рис. 24.8), спроектирован специалистами фирмы «Спайн роботикс». В нем используется длинный хоботоподобный манипулятор, состоящий из множества чечевицеобразных дисков, которые соединены между собой двумя парами тросов, обеспечивающих натяжение. Тросы соединены с поршнями гидравлических цилиндров, которые, создавая натяжение, вызывают перемещение манипулятора. Специальные датчики передают на систему управления информацию о положении манипулятора и его кисти. Такой робот отличается чрезвычайно большой гибкостью, значительным радиусом действия и высокой маневренностью.
Другой робот маятникового типа, IR B1000, разработан специалистами фирмы ASEA; его манипулятор подвешен подобно маятнику с двойным карданным подвесом и может перемещаться по направляющим относительно продольной и поперечной осей. По утверждению специалистов фирмы ASEA, это устройство движется в 1,5 раза быстрее, чем традиционные манипуляторы, что обеспечивает высокую производительность.
Кинематическая цепь, реализующая локальные движения, называется кистью робота, поскольку она выполняет функции, аналогичные функциям кисти руки человека. Назначение кисти - обеспечить ориентирующие движения. Для удержания объекта манипулирования кисть снабжается схватом. Существует столько же типов схватов, сколько и областей применения роботов. Конструкции схватов могут представлять собой устройства от обыкновенных клещей для захвата предметов двумя или несколькими губками до специально сконструированных схватов, в гнезда которых устанавливаются сменные инструменты для выполнения ряда технологических операций, таких, как сверление, нарезание резьбы, сварка, резка, окраска и т. д.
Рассмотрим основные геометро-кинематические и структурные характеристики манипуляторов, к которым прежде всего относят число степеней подвижности, форму и размеры рабочей зоны, маневренность, угол и коэффициент сервиса.
Число степеней подвижности схвата манипулятора можно подсчитать как сумму подвижностей всех пар открытой кинематической цепи. Сказанное не противоречит формуле Малышева (3.1) для пространственных механизмов, так как в открытых цепях число подвижных звеньев всегда равно числу кинематических пар.
Для рассмотренных механизмов манипуляторов с одноподвижными парами (рис. 24.3 - 24.7) можно использовать формулу:
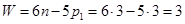 ,
,
где n - число подвижных звеньев; 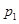 - число одноподвижных пар.
- число одноподвижных пар.
|
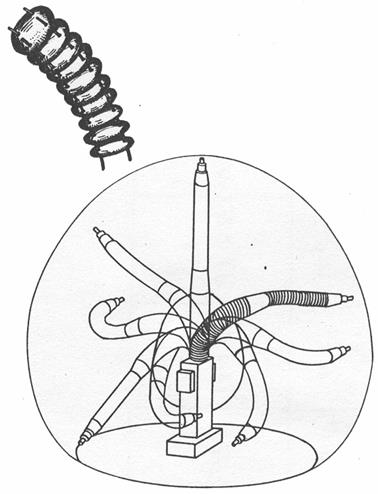 Под маневренностью манипулятора понимают число его степеней подвижности при неподвижном схвате. Маневренность характеризует возможность кинематической цепи манипулятора занимать разные положения при одном и том же положении схвата. Маневренность манипулятора зависит не только от вида и числа кинематических пар, но и от их расположения. Так, манипулятор, изображенный на рис. 24.9, а, имеет маневренность, равную единице, - это групповая подвижность, означающая возможность совместного вращения звеньев 1, 2 вокруг оси АС, проходящей через центры сферических пар. Маневренность, равная единице, в этом случая означает, что к заданной точке Е в заданном направлении СЕ схват может подойти при различных положениях остальных звеньев 1, 2, геометрическим местом которых будут конические поверхности с вершинами в точках А и С и образующими АВ и СВ.
Под маневренностью манипулятора понимают число его степеней подвижности при неподвижном схвате. Маневренность характеризует возможность кинематической цепи манипулятора занимать разные положения при одном и том же положении схвата. Маневренность манипулятора зависит не только от вида и числа кинематических пар, но и от их расположения. Так, манипулятор, изображенный на рис. 24.9, а, имеет маневренность, равную единице, - это групповая подвижность, означающая возможность совместного вращения звеньев 1, 2 вокруг оси АС, проходящей через центры сферических пар. Маневренность, равная единице, в этом случая означает, что к заданной точке Е в заданном направлении СЕ схват может подойти при различных положениях остальных звеньев 1, 2, геометрическим местом которых будут конические поверхности с вершинами в точках А и С и образующими АВ и СВ.
 Если пары А к В поменять местами (рис. 24.9, б), то число степеней подвижности по формуле Малышева останется прежним:
Если пары А к В поменять местами (рис. 24.9, б), то число степеней подвижности по формуле Малышева останется прежним:
но это местная подвижность, означающая возможность вращения звена 2 вокруг оси ВС, при этом маневренность будет равна нулю, поскольку в данном случае схват может подойти к заданной точке Е рабочей зоны в заданном направлении СЕ только при одном единственном положении звеньев 1, 2.
Повышенная маневренность увеличивает возможности для выполнения сложных операций с объектом манипулирования наиболее рациональным путем в условиях наличия препятствий в рабочей зоне, но усложняет задачу управления таким роботом, поскольку приводит к неоднозначному решению задачи расчета обобщенных координат.
|
Исполнительным устройством называют устройство, выполняющее все двигательные функции робота.
Рабочий орган - составная часть исполнительного устройства для непосредственного выполнения технологических операций или вспомогательных переходов.
Рабочее пространство манипулятора - часть физического пространства, в котором может находиться исполнительное устройство при функционировании манипулятора.
Рабочая зона - пространство, в котором может находиться рабочий орган. Не в любой точке рабочей зоны схват может занимать произвольное положение из-за конструктивных ограничений на углы поворота в шарнирах, поэтому рабочая зона реально уменьшается до зоны обслуживания.
Зона обслуживания - пространство, в котором рабочий орган выполняет свои функции в соответствии с назначением.
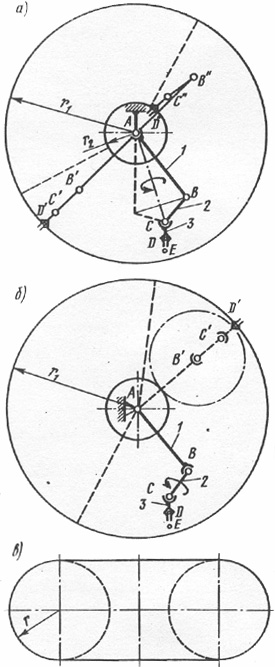
Для манипулятора, изображенного на рис. 24.9, а, рабочая зона - пространство между сферами радиусом 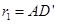 и радиусом
и радиусом 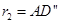 , а зона обслуживания лишь часть такого пространства (штриховая линия на рис. 24.9, а); для манипулятора, изображенного на рис. 24.9, б, рабочая зона - тор (кольцо кругового сечения) с размерами
, а зона обслуживания лишь часть такого пространства (штриховая линия на рис. 24.9, а); для манипулятора, изображенного на рис. 24.9, б, рабочая зона - тор (кольцо кругового сечения) с размерами 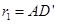 и
и 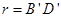 (рис. 24.9, в), а зона обслуживания - часть такого тора (штрихованная линия на рис. 24.9, б).
(рис. 24.9, в), а зона обслуживания - часть такого тора (штрихованная линия на рис. 24.9, б).
Манипулятор с тремя поступательными парами (см. рис. 24.3) имеет рабочую зону в виде прямоугольного параллелепипеда. Для манипулятора с одной вращательной и двумя поступательными парами (см. рис. 24.4) рабочая зона - кольцевой цилиндрический сектор.
В общем случае для каждой точки рабочей зоны манипулятора существует некоторый телесный угол 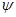 - угол сервиса, внутри которого схват может подойти к этой точке. Как известно, величина телесного угла определяется отношением площади сферы, вырезанной телесным углом, к квадрату радиуса сферы, поэтому максимальное значение телесного угла
- угол сервиса, внутри которого схват может подойти к этой точке. Как известно, величина телесного угла определяется отношением площади сферы, вырезанной телесным углом, к квадрату радиуса сферы, поэтому максимальное значение телесного угла 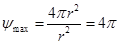 ср (стерадиан).
ср (стерадиан).
Отношение угла 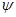 к его максимальному значению
к его максимальному значению 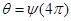 называют коэффициентом сервиса в данной точке. Величина в может изменяться от нуля для точек на границе рабочей зоны, где схват может быть подведен в единственном направлении, до единицы для точек зоны полного сервиса, где схват может быть подведен в любом направлении.
называют коэффициентом сервиса в данной точке. Величина в может изменяться от нуля для точек на границе рабочей зоны, где схват может быть подведен в единственном направлении, до единицы для точек зоны полного сервиса, где схват может быть подведен в любом направлении.
Определение значения коэффициента сервиса 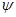 связано с анализом движения звеньев механизма манипулятора при различных фиксированных положениях центра схвата.
связано с анализом движения звеньев механизма манипулятора при различных фиксированных положениях центра схвата.
Методику вычисления 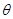 рассмотрим на примере манипулятора с двумя сферическими и одной вращательной парами (рис. 24.9, а). Для определения угла сервиса
рассмотрим на примере манипулятора с двумя сферическими и одной вращательной парами (рис. 24.9, а). Для определения угла сервиса 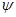 в некоторой точке Е рабочей зоны рассмотрим механизм манипулятора как пространственный четырехзвенник со сферическими парами А, С, D и вращательной парой В; точка D центра схвата совпадает с заданной точкой Е на линии 4 (рис 24.10, а). Сперва определим возможные положения звена CD (схвата) в плоскости чертежа, а затем все его возможные положения в пространстве путем вращения плоского четырехзвенника относительно условной стойки AD длиной r, совпадающей с осью х пространственной системы координат Oxyz.
в некоторой точке Е рабочей зоны рассмотрим механизм манипулятора как пространственный четырехзвенник со сферическими парами А, С, D и вращательной парой В; точка D центра схвата совпадает с заданной точкой Е на линии 4 (рис 24.10, а). Сперва определим возможные положения звена CD (схвата) в плоскости чертежа, а затем все его возможные положения в пространстве путем вращения плоского четырехзвенника относительно условной стойки AD длиной r, совпадающей с осью х пространственной системы координат Oxyz.
В области, где коэффициент сервиса  , угол сервиса
, угол сервиса 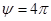 . Следовательно, точка С должна иметь возможность занять любое положение на сфере радиусом
. Следовательно, точка С должна иметь возможность занять любое положение на сфере радиусом  с центром в точке D. Для этого в плоском четырехзвеннике звено CD должно быть кривошипом, т. е. поворачиваться на полный оборот. Как известно (см. лекцию N5) условие существования кривошипа состоит в том, что сумма длин самого короткого и самого длинного звеньев должна быть меньше суммы длин остальных звеньев. Если, например, звено 1 самое длинное, а звено 3 самое короткое, то
с центром в точке D. Для этого в плоском четырехзвеннике звено CD должно быть кривошипом, т. е. поворачиваться на полный оборот. Как известно (см. лекцию N5) условие существования кривошипа состоит в том, что сумма длин самого короткого и самого длинного звеньев должна быть меньше суммы длин остальных звеньев. Если, например, звено 1 самое длинное, а звено 3 самое короткое, то 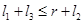 , откуда
, откуда 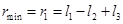 (см. рис.2.4.10, б).
(см. рис.2.4.10, б).
Если самое длинное звено 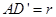 , а самое короткое звено 3, то
, а самое короткое звено 3, то 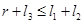 , откуда
, откуда 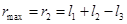 .
.
В пределах от  , до
, до  коэффициент сервиса
коэффициент сервиса  (зона II на рис. 24.10, б).
(зона II на рис. 24.10, б).
Если же Звено 3 является коромыслом, то 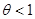 . В предельных положениях, когда звенья 1, 2, 3 находятся на одной прямой Ах,
. В предельных положениях, когда звенья 1, 2, 3 находятся на одной прямой Ах, 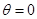 . Это имеет место при
. Это имеет место при 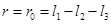 и при
и при 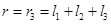 . Следовательно, в зонах I и III на рис.24.10, б,
. Следовательно, в зонах I и III на рис.24.10, б,  .
.
|
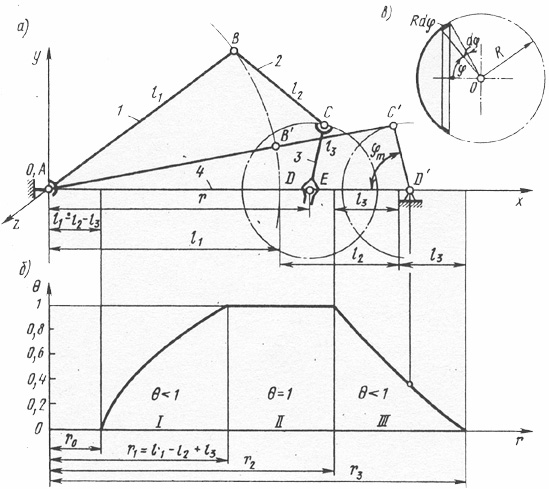 В любой промежуточной точке зон I или III, например в точке
В любой промежуточной точке зон I или III, например в точке  , можно определить коэффициент сервиса
, можно определить коэффициент сервиса  следующим образом. Найдя максимально возможный угол поворота
следующим образом. Найдя максимально возможный угол поворота 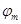 , коромысла
, коромысла 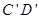 , когда звенья АВ' и В'С' находятся на одной прямой, определим поверхность сферического сектора радиусом
, когда звенья АВ' и В'С' находятся на одной прямой, определим поверхность сферического сектора радиусом 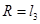 и углом
и углом 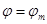 (рис. 24.10, в). Формулу поверхности S шарового сектора получим путем суммирования элементарных поверхностей
(рис. 24.10, в). Формулу поверхности S шарового сектора получим путем суммирования элементарных поверхностей 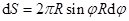 в пределах от
в пределах от 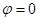 до
до 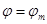 .
.
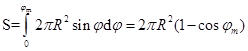
В нашем случае 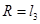 и
и 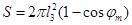 ; следовательно,
; следовательно,
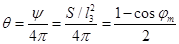
На рис. 24.10, а при 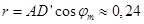 коэффициент сервиса
коэффициент сервиса 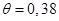 . График зависимости для манипулятора с размерами звеньев, изображенных на рис. 24.10, а, представлен на рис. 24.10, б. Подобные графики нужны не только при исследовании имеющегося манипулятора, но и при проектировании кинематических схем манипуляторов по заданным условиям.
. График зависимости для манипулятора с размерами звеньев, изображенных на рис. 24.10, а, представлен на рис. 24.10, б. Подобные графики нужны не только при исследовании имеющегося манипулятора, но и при проектировании кинематических схем манипуляторов по заданным условиям.
К техническим показателям, характеризующим промышленные роботы, также относятся грузоподъемность, быстродействие, точность позиционирования, энергетические затраты и т. д.
Задачи о положениях манипуляторов.
 |
При решении задач проектирования и управления промышленными роботами приходится определять как положения его звеньев относительно неподвижной системы координат (абсолютные положения звеньев), так и их относительные положения (например, обобщенные координаты). Соответственно эти задачи известны в робототехнике как прямая и обратная задачи о положениях.
|
 обычно связывается со стойкой, а с каждой кинематической парой связывается подвижная система координат, одна из осей которой связана с характерными признаками звена, например осевой линией. Для
обычно связывается со стойкой, а с каждой кинематической парой связывается подвижная система координат, одна из осей которой связана с характерными признаками звена, например осевой линией. Для
|
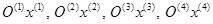 , (или
, (или  ) четырехзвенной открытой кинематической цепи из звеньев 1, 2, 3, 4, моделирующей структуру руки человека (см. рис. 24.2, б). Ось
) четырехзвенной открытой кинематической цепи из звеньев 1, 2, 3, 4, моделирующей структуру руки человека (см. рис. 24.2, б). Ось 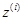 направляют вдоль оси кинематической пары, а ось
направляют вдоль оси кинематической пары, а ось 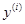 дополняет правую систему координат
дополняет правую систему координат 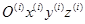
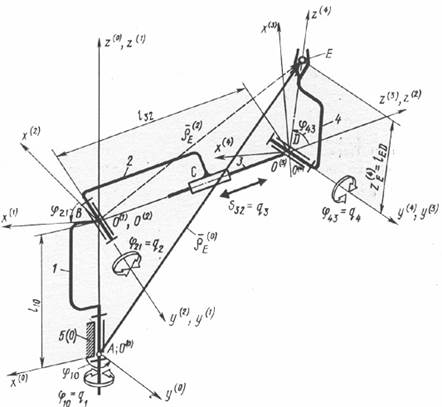
Применение метода преобразования координат для решения прямой задачи о положениях проиллюстрируем на примере кинематической схемы промышленного робота (рис. 25.1). Четыре подвижных звена 1, 2, 3 и 4 образуют четыре одноподвижные пары, из которых три вращательные и одна поступательная. Число степеней подвижности робота равно четырем:
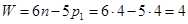
Поэтому для решения прямой задачи о положениях должны быть заданы четыре обобщенные координаты: относительные углы поворота звеньев 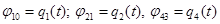 и относительное перемещение вдоль оси звена 3
и относительное перемещение вдоль оси звена 3 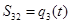 (рис. 25.1).
(рис. 25.1).
Требуется определить радиус-вектор 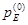 точки Е схвата относительно неподвижной системы координат
точки Е схвата относительно неподвижной системы координат 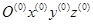 , связанной со стойкой 5 (или 0). Оси систем координат ориентированы относительно элементов кинематических пар следующим образом:
, связанной со стойкой 5 (или 0). Оси систем координат ориентированы относительно элементов кинематических пар следующим образом:
ось 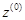 неподвижной системы координат стоики направлена вдоль оси вращательной пары А;
неподвижной системы координат стоики направлена вдоль оси вращательной пары А;
со звеном 1 связана система 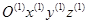 , имеющая смещение
, имеющая смещение  начала координат
начала координат 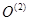 вдоль оси
вдоль оси 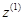 . Ось
. Ось 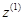 совпадает с осью
совпадает с осью 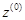 , а ось
, а ось 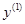 направлена по оси вращательной кинематической пары В;
направлена по оси вращательной кинематической пары В;
со звеном 2 связана система 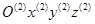 , имеющая начало координат
, имеющая начало координат 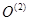 совпадающее с точкой
совпадающее с точкой  . Ось
. Ось 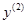 совпадает с осью
совпадает с осью 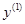 т. е. с осью вращательной кинематической пары В;
т. е. с осью вращательной кинематической пары В;
начало координат системы 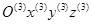 имеет смещение
имеет смещение 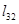 относительно точки
относительно точки 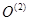 вдоль оси
вдоль оси 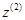 . Ось
. Ось  выбрана совпадающей с осью
выбрана совпадающей с осью 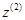 ;
;
координата 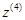 точки Е схвата 4 задана в системе
точки Е схвата 4 задана в системе 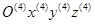 , ось
, ось 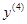 которой направлена по оси вращательной кинематической пары D.
которой направлена по оси вращательной кинематической пары D.
Для определения радиуса-вектора  необходимо разрешить матричное уравнение перехода к системе координат
необходимо разрешить матричное уравнение перехода к системе координат 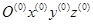 :
:
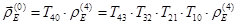 (25.1)
(25.1)
Достоинство метода проявляется в случае специального выбора подвижных систем координат. Если координатные оси совмещать с осью вращательной пары или направлением поступательной пары, то матрицы перехода существенно упрощаются.
Координаты точки Е в трехмерном пространстве записываются в виде столбцевых матриц:
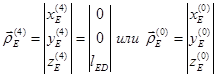
Здесь  - матрица перехода от системы
- матрица перехода от системы  к системе
к системе  (элементарная матрица поворота вокруг оси z и перемещения вдоль оси z):
(элементарная матрица поворота вокруг оси z и перемещения вдоль оси z):
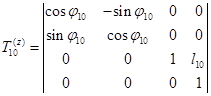 ;
;
 - матрица перехода от системы
- матрица перехода от системы 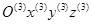 к системе
к системе 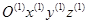 (элементарная матрица поворота относительно оси y):
(элементарная матрица поворота относительно оси y):
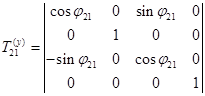 ;
;
 - матрица перехода от системы
- матрица перехода от системы 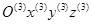 к системе
к системе 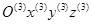 (элементарная матрица перемезения вдоль оси x):
(элементарная матрица перемезения вдоль оси x):
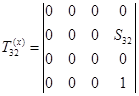 ;
;
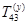 - матрица перехода от системы
- матрица перехода от системы 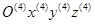 к системе
к системе 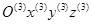 (элементарная матрица поворота вокруг оси x):
(элементарная матрица поворота вокруг оси x):
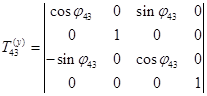 .
.
Подставив эти матрицы в формулу (25.1), получим координаты точки Е в системе 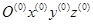 . Развернутые формулы, определяющие положение точки Е схвата, ввиду громоздкости не приведены. При решении конкретных задач на ЭВМ целесообразно воспользоваться библиотекой стандартных подпрограмм для выполнения элементарных операций с матрицами.
. Развернутые формулы, определяющие положение точки Е схвата, ввиду громоздкости не приведены. При решении конкретных задач на ЭВМ целесообразно воспользоваться библиотекой стандартных подпрограмм для выполнения элементарных операций с матрицами.
Для определения скорости и ускорения точек звеньев пространственных механизмов манипуляторов при использовании метода преобразования координат имеют в виду, что радиус-вектор 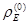 , например, точки Е есть векторная функция обобщенных координат:
, например, точки Е есть векторная функция обобщенных координат:
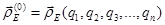
поэтому скорость 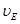 точки Е определяется по соотношению
точки Е определяется по соотношению
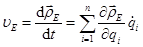 , (25.2)
, (25.2)
или
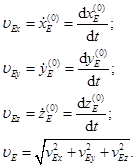 (25.3)
(25.3)
Абсолютную угловую скорость j-го звена относительно стойки находят сложением угловых скоростей при относительном движении звеньев:
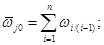 (25.4)
(25.4)
индекс i(i - 1) указывает на порядковые номера звеньев, участвующих в относительном движении, например
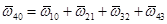
Решения обратных задач о положениях манипуляторов в явном виде имеют важное значение как при проектировании, так и при управлении. При проектировании такие решения позволяют оценить влияние конструктивных параметров на процесс движения, при управлении - построить быстродействующие алгоритмы управления.
Контрольные вопросы к лекциям 24, 25
1. Что такое манипулятор, автооператор, промышленный робот?
2. Для чего предназначены промышленные роботы?
3. В чём заключаются особенности структуры кинематических цепей манипуляторов промышленных роботов?
4. От чего зависят двигательные возможности манипулятора промышленного робота?
5. Что такое подвижность манипулятора ? Как она определяется?
6. Дайте определение рабочего пространства, зоны обслуживания манипулятора и его маневренности (на любом примере)
| <== предыдущая лекция | | | следующая лекция ==> |
| характеристики манипуляторов. | | | ЛЕКЦИЯ 12 |
Дата добавления: 2015-03-14; просмотров: 4800;
