Краткая теория. Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями (например

Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями (например, вблизи границ непрозрачных или прозрачных тел, сквозь малые отверстия и т.п.) и связанных с отклонениями от законов геометрической оптики. Дифракция, в частности, приводит к огибанию волнами препятствий, соизмеримых с длиной волны, и проникновению света в область геометрической тени.

Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. Перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть интерференцией волн. Перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, принято называть дифракцией света.

Различают два вида дифракции. Если источник света S и точка наблюдения Р расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку Р, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера. В противном случае говорят о дифракции Френеля.

Проникновение световых волн в область геометрической тени может быть объяснено с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волновое движение, служит центром вторичных волн (в изотропной и однородной среде они будут сферическими). Огибающая этих волн дает положение фронта волны в следующий момент времени.

Однако этот принцип не дает сведений об амплитуде, а, следовательно, и об интенсивности волн, распространяющихся в различных направлениях. Френель дополнил принцип Гюйгенса представлением интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. Развитый таким способом принцип Гюйгенса получил название принципа Гюйгенса – Френеля.

Согласно принципу Гюйгенса – Френеля каждый элемент волновой поверхности служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS. Амплитуда сферической волны убывает с расстоянием r от источника по закону 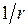. Следовательно, от каждого участка dS волновой поверхности в точку Р, лежащую перед этой поверхностью, приходит колебание

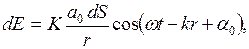
где 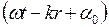– фаза колебаний в месте расположения волновой поверхности S,

k – волновое число,

а₀ – определяется амплитудой светового колебания в том месте, где находится dS.

Коэффициент пропорциональности К зависит от угла 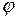между нормалью n к площадке dS и направлением от dS к точке Р. При 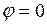этот коэффициент максимален, при 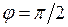он обращается в нуль.

Результирующее колебание в точке Р представляет собой суперпозицию колебаний, взятых для всей волновой поверхности S:

.

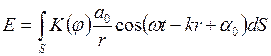Эта формула является аналитическим выражением принципа Гюйгенса – Френеля.

Для наблюдения дифракционной картины в данной работе используется дифракционная решетка – совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей. Дифракционная решетка имеет две характеристики, которые связаны между собой следующим соотношением:

,

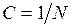где N – число штрихов на 1 мм,

С – постоянная (период) решетки.

Постоянная решетки равна сумме ширины прозрачного промежутка а и непрозрачного штриха в: С=а+в.

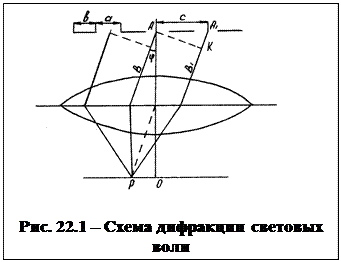
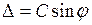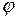Выясним характер дифракционной картины, получающейся на экране при нормальном падении на решетку плоской световой волны (рис. 22.1). Из рисунка 22.1 видно, что разность хода от соседних щелей (отрезок А₁К) , где – угол отклонения луча от первоначального направления. Следовательно, в точках, в которых выполняется условие

,

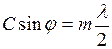колебания взаимно усиливают друг друга, если m – четное, и ослабляют, если m – нечетное ( 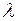– длина волны падающего излучения).

Результирующее колебание в точке Р дифракционной картины, положение которой определяется углом 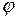, представляет собой сумму N колебаний с одинаковой амплитудой 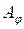, сдвинутых друг относительно друга по фазе на одну и ту же величину 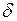. Интенсивность при этих условиях равна

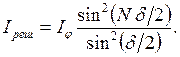
Из рисунка 22.1 видно, что разность хода от соседних щелей равна 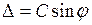. Следовательно, разность фаз

,

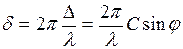где 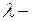длина волны в данной среде.

Окончательное выражение для интенсивности имеет:

.

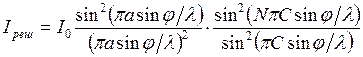Первый множитель обращается в нуль в точках, для которых

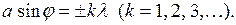(22.1)

В этих точках интенсивность, создаваемая каждой из щелей в отдельности, равна нулю. Это условие определяет положение минимумов интенсивности.

Второй множитель принимает значение 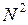в точках, удовлетворяющих условию

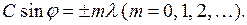(22.2)

Это условие определяет положение максимумов интенсивности, называемых главными. Число m дает порядок главного максимума. Максимум нулевого порядка только один, остальных по два.

Кроме минимумов, определяемых условием (22.1), в промежутках между соседними главными максимумами имеется по (N–1) добавочных минимума. Эти минимумы возникают в том направлении, для которых колебания от соседних щелей погашают друг друга. Направления добавочных минимумов определяется условием:

,

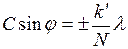
т.е. 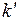принимает все целочисленные значения, кроме 0, N, 2N,… т.к. при этих значениях это условие переходит в условие (22.2).

Из условия, определяющего положение главных максимумов (22.2), следует, что

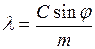. (22.3)

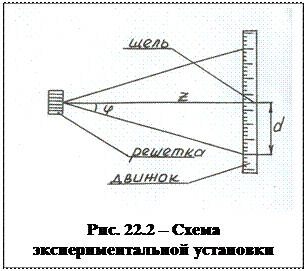
Эта формула лежит в основе способа определения длины волны в данной работе.