Вывод расчетных формул. В данной работе рассматривается скатывание тел с наклонной плоскости (рис

В данной работе рассматривается скатывание тел с наклонной плоскости (рис. 1.1). Если угол a наклона плоскости мал, то при движении отсутствует скольжение. Между телом и плоскостью в точках их соприкосновения возникает трение, являющееся трением покоя. Так как эти точки в каждый момент времени неподвижны, то сила трения, действующая на катящееся тело, работы не совершает. Поэтому полная энергия катящегося тела остается постоянной.

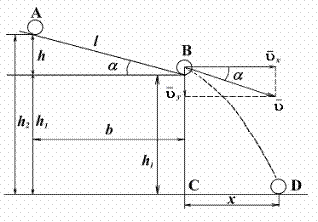
Рис. 1.1.

Поскольку тело совершает вращение и его центр масс, через который проходит ось вращения, перемещается поступательно, кинетическая энергия складывается из энергии поступательного и вращательного движений.

Согласно закону сохранения механической энергии, потенциальная энергия тела на вершине плоскости (в точке А) равна сумме кинетической энергии поступательного движения тела 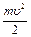и кинетической энергии вращательного движения тела :

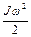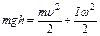, (1.1)

где m – масса скатывающегося тела;

g – ускорение свободного падения;

h – высота наклонной плоскости (h = h₂ – h₁);

u – линейная скорость центра масс тела в точке В;

I – момент инерции тела относительно оси вращения;

w – угловая скорость вращения тела.

Так как скольжение отсутствует, то

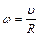, (1.2)

где R – радиус катящегося тела.

Из формул (1.1) и (1.2) следует, что

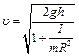. (1.3)

Момент инерции тел, обладающих симметрией вращения, можно записать в виде

,

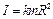где k – безразмерный коэффициент.

Так, для шара

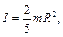
тогда

;

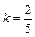для тонкостенного полого цилиндра

I = mR²,

тогда

;

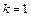для сплошного цилиндра

,

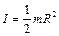тогда

.

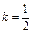Учитывая, что

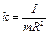, (1.4)

получим формулу для скорости тела в точке В:

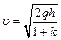. (1.5)

Движение тела по наклонной плоскости будет равноускоренным, так как происходит под действием постоянной силы – силы тяжести. Для равноускоренного движения без начальной скорости

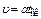; (1.6)

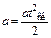, (1.7)

где l – длина пути по наклонной плоскости;

а – ускорение центра масс тела;

t_ск – время скатывания тела по наклонной плоскости АВ.

Из выражений (1.6) и (1.7) следует, что

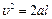, (1.8)

тогда из формул (1.5) и (1.8) получим:

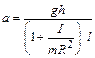, (1.9)

или

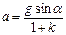. (1.10)

Время скатывания тела по наклонной плоскости АВ определим из формул (1.5), (1.6), (1.10):

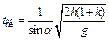. (1.11)

Из формул (1.5), (1.10), (1.11) видно, что u, t_ск и а зависят от формы тела (коэффициент k) и не зависят от его массы и размеров.

Скорость тела в точке В можно также определить из законов движения тела по траектории BD. Для этого вектор скорости 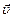разложим на вертикальную 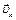и горизонтальную 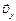составляющие. Движение по параболе BD можно рассматривать как равномерное в горизонтальном направлении с постоянной скоростью 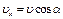и равноускоренное в вертикальном направлении с начальной скоростью 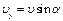и ускорением g. Путь при равномерном движении определяется по формуле

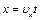, (1.12)

а при равноускоренном –

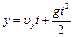, (1.13)

где t – время свободного полета тела по кривой BD;

х – горизонтальная дальность полета тел;

у – путь, проходимый телом по вертикали ВС.

Подставляя значения u_x и u_у в уравнения (1.12) и (1.13), получим:

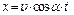; (1.14)

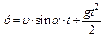. (1.15)

Выразив из уравнения (1.14) время:

,

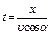и подставив в формулу (1.15), получим:

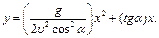(1.16)

Полученное уравнение есть уравнение параболы. Таким образом, тело, скатившись с наклонной плоскости, дальше движется по ветви параболы BD.

Из уравнения (1.16) найдем скорость тела в точке В по экспериментальным данным. Обозначим эту скорость :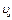

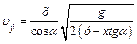. (1.17)