Общие сведения. На рис. 9 представлена электрическая цепь однофазного синусоидального напряжения с параллельным соединением двух приемников
На рис. 9 представлена электрическая цепь однофазного синусоидального напряжения с параллельным соединением двух приемников, один их которых на схеме замещен последовательным соединением резистора и емкостного элемента, а второй – последовательным соединением резистора и индуктивного элемента. Токи в приемниках определяются по закону Ома:
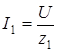 ;
; 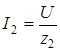 ,
,
| где | 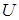
| - действующее значение напряжения источника электрической энергии; |
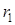 , , 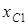 , , 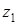
| - активное, емкостное и полное сопротивления первого приемника; | |
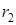 , , 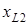 , , 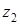
| - активное, индуктивное и полное сопротивления второго приемника; |
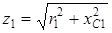 ,
, 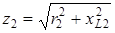 .
.
Вектор тока источника электрической энергии равен сумме векторов токов приемников:
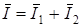 .
.
Векторная диаграмма напряжения и токов для рассматриваемой схемы приведена на рис. 10.
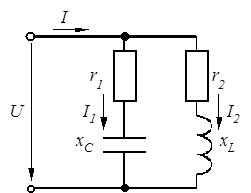 Рис. 9
Рис. 9
| 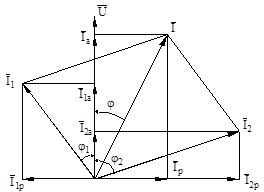 Рис. 10
Рис. 10
|
Энергетические процессы в электрической цепи характеризуются величинами активной 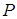 , реактивной
, реактивной 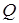 и полной
и полной 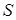 мощности, а также коэффициентом мощности
мощности, а также коэффициентом мощности 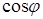 .
.
Для первого приемника
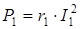 ,
, 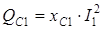 ,
, 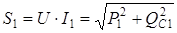 ,
, 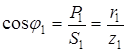 .
.
Для второго приемника
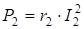 ,
, 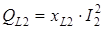 ,
, 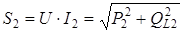 ,
, 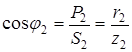 .
.
Для двух приемников
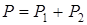 ,
, 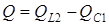 ,
, 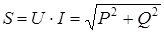 ,
, 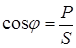 .
.
В соответствии с балансом активной и реактивной мощностей под 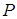 ,
, 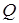 ,
, 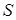 ,
, 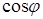 следует понимать также активную, реактивную и полную мощности источника электрической энергии и его коэффициент мощности.
следует понимать также активную, реактивную и полную мощности источника электрической энергии и его коэффициент мощности.
При исследовании процессов в цепях с параллельным соединением приемников вектор тока в каждой ветви условно представляют в виде суммы векторов активной и реактивной составляющих тока. Вектор активной составляющей тока 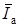 совпадает по направлению с вектором напряжения
совпадает по направлению с вектором напряжения 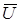 , а вектор реактивной составляющей
, а вектор реактивной составляющей 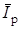 перпендикулярен этому вектору.
перпендикулярен этому вектору.
Величины активной и реактивной составляющих токов приемников (см. рис. 10)
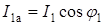 ;
; 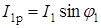 ;
;
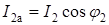 ;
; 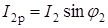 ,
,
где 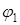 и
и 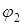 - углы сдвига фаз между вектором напряжения
- углы сдвига фаз между вектором напряжения 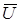 и векторами токов
и векторами токов 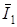 и
и 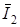 .
.
Представление токов активными и реактивными составляющими позволяет путем их сложения найти активную 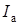 и реактивную
и реактивную 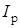 составляющие тока источника и по ним определить ток источника
составляющие тока источника и по ним определить ток источника 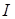 .
.
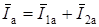 ;
; 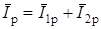 ;
; 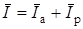 .
.
Из векторной диаграммы рис. 10, следует:
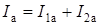 ;
; 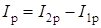 ;
; 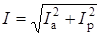 .
.
Косинус угла сдвига фаз между вектором тока источника 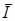 и вектором напряжения источника
и вектором напряжения источника 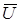 определяется из выражения
определяется из выражения
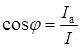 .
.
В электрических цепях с параллельным соединением приемников, содержащих индуктивные и емкостные элементы, может, при определенных условиях, возникать явление резонанса токов. Резонансом токов называется режим, при котором ток источника электрической энергии совпадает по фазе с напряжением источника, т.е. 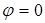 . Следовательно, условием резонанса токов является равенство нулю реактивной мощности цепи и реактивной составляющей тока источника электрической энергии.
. Следовательно, условием резонанса токов является равенство нулю реактивной мощности цепи и реактивной составляющей тока источника электрической энергии.
Применительно к электрической цепи, изображенной на рис. 9,
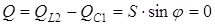 ;
; 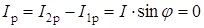 .
.
Из условия резонанса токов следует, что
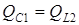 ;
; 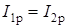 .
.
При резонансе токов коэффициент мощности цепи
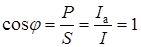 .
.
Ток в ветви с источником электрической энергии содержит только активную составляющую, является минимальным по величине и может оказаться значительно меньше токов в каждом из параллельно включенных приемников:
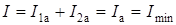 .
.
Дата добавления: 2015-01-13; просмотров: 1085;
