О приближенных вычислениях.

Численные значения величин, которыми приходится оперировать при решении физических задач, являются приближенными. Поэтому, при вычислениях необходимо соблюдать следующие правила:

1. Достаточно производить вычисления с числами, содержащими не более знаков, чем в исходных данных, так как с помощью вычислений невозможно получить результат более точный, чем исходные данные.

2. При сложении и вычитании чисел, имеющих разную точность, более точное округляется до менее точного. Например: 9.6 + 0.176 = 9.6 + 0.2 = 9.8; 100.83 – 0.4 = 100.8 – 0.4 = 100.4.

3. При умножении и делении результат следует округлять так, чтобы он содержал столько значащих цифр, сколько их имеет сомножитель с наименьшим числом значащих цифр. Например: 342×378=129×10³; 0.352:0.301=0.117.

4. При извлечении корня результат должен иметь столько значащих цифр, сколько их имеет подкоренное выражение. Например: .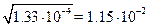

5. При вычислении сложных выражений выполняются правила в зависимости от производимых действий.

6. Если угол α<0.2 радиан, то sin α = tg α = α.

×