Измерение расстояний до навигационных спутников

«GPS»

В связи с тем, что любая «GPS» основана на определении расстояний до навигационных спутников, очевидно должны быть разработаны и со­ответствующие методы их определения.

Основной принцип определения расстояний до навигационных спут­ников состоит в измерении времени, за которое радиосигнал спутника достигает приемника на Земле, и в последующем вычислении по этому времени искомого расстояния.

Поскольку радиоволны распространяются с огромной скоростью, т. е. со скоростью света (около 300 000 км/с), нужно уметь очень точно определять момент выдачи сообщения навигационным спутником и мо­мент его приема приемником «GPS» на Земле. Очевидно разница (сдвиж­ка) во времени выдачи сигнала спутником и его приемом на Земле даст время распространения сигнала а, следовательно, и расстояние до данно­го спутника. При таком подходе часы в системе должны быть исключи­тельно точными и совершенными. Действительно, при ошибке в опреде­лении времени распространения радиосигнала всего на 0,01 с, ошибка в определении расстояния составит порядка 3000 км.

На каждом навигационном спутнике, в связи с этим, установлен ком­плект из 4-х самых точных атомных часов, которые чрезвычайно дороги и громоздки. На всех приемниках «GPS» вынужденно, устанавливают очень дешевые и компактные кварцевые часы, которые, однако, сущест­венно уступают по точности хода атомным.

Главной трудностью определения времени распространения радио­сигнала является точное выделение момента, времени, в которое радио­сигнал был передан со спутника. В системах «GPS» эта задача решена синхронизацией сигналов навигационных спутников в Космосе и прием­ников «GPS» на Земле таким образом, чтобы они точно в одно и то же вре­мя генерировали один и тот же бинарный (двоичный) код. Бинарный код — это очень сложная, тщательно подобранная и кажущаяся случайной последовательность логических нулей и единиц, которая повторяется ка­ждую миллисекунду. Такие специально усложненные коды (для надеж­ности и однозначности их сравнения) называют псевдослучайными кода­ми (рис. 8.6).

Учитывая, что псевдослучайные коды на спутниках и приемниках строго синхро­низированы, для определения времени рас­пространения радиосигнала и, следова­тельно, расстояния до данного спутника, достаточно принять от него радиосигнал и сопоставить его с точно таким же псевдослучайным кодом приемника. Сдвиг одного кода по отношению к другому будет соответствовать вре­мени прохождения радиосигнала от навигационного спутника до прием­ника «GPS» (рис. 8.7).

Поскольку точность измерения времени распространения радиосиг­нала кварцевыми часами приемников существенно уступает точности хода атомных часов навигационных спутников, возникает проблема уст­ранения смещения шкалы времени приемников «GPS».

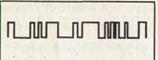
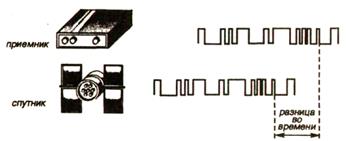Рис. 8.6. Псевдослу- Рис. 8.7. Определение времени

чайный код. распространения радиосигнала

по сдвижке псевдослучайных

кодов.

Можно легко установить, что если три точных измерения времени распространения радиосигналов спутников позволяют определить точ­ное местоположение точки в трехмерном пространстве, то же самое обеспечивают четыре неточных измерения времени.

Для облегчения понимания этого принципа рассмотрим решение этой задачи в двухмерном пространстве, т. е. на плоскости, временно исклю­чив одно измерение.

Представим себе, что мы находимся на расстоянии в 4 с от спутника А и в 6 с от спутника В. Этих двух точных измерений было бы достаточно для однозначного определения местоположения точки 1 на плоскости (рис. 8.8, точка 1).

Таким образом, местоположение точки 1 было бы установлено, если бы часы приемников «GPS» были бы столь же совершенны, как и атом­ные часы на навигационных спутниках. Теперь представим себе, что ус­ловно часы в приемниках отстают на одну секунду. Тогда расстояния до искомой точки были бы установлены с соответствующими ошибками и составили соответственно до спутника А — 5 с и до спутника В — 7 с. В результате положение искомой точки 1 было бы ошибочно определено в точке 2 (рис. 8.8, точка 2).

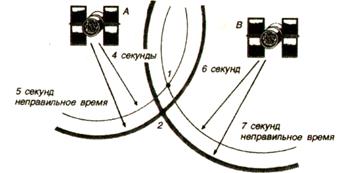
Рис. 8.8. Определение местоположения точки на плоскости по двум измерениям: 1 — по двум точным измерениям; 2 — ошибочное определение местоположения точки по двум неточным измерениям.

Следует иметь в виду, что внешне это бы выглядело абсолютно пра­вильным результатом, поскольку у нас нет возможности установить, что часы приемника отстают.

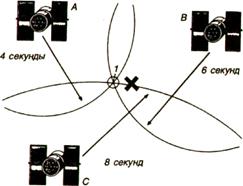
Если к этим построениям добавить еще одно измерение, что в двухмерном пространстве означает измерение расстояния до спутника С, рав­ного, скажем, 8 с, то все три точных измерения дадут положение искомой точки 1 на пересечении трех соответствующих окружностей (рис. 8.9).

Если учесть, что часы приемника несколько отстают, то в результате трех неточных измерений будут получены три возможных местоположе­ния одной искомой точки (точки 2, 3 и 4), которая может одновременно находиться на расстояниях 5, 7 и 9 с соответственно от спутников А, В и С, что физически невозможно (рис. 8.10).

Рис. 8.9. Определение местоположения точки 1 на плоскости