Космические скорости.
спутники Земли подчиняются тем же законам, что и естественные, но их орбиты имеют некоторые особенности.
ИСЗ выводятся на орбиту с помощью многоступенчатых ракет. Последняя ступень ракеты сообщает спутнику определённую скорость на заданной высоте h от поверхности Земли. Тело станет ИСЗ, если его скорость будет достаточной.
Если скорость запуска точно равна круговой скорости на данной высоте h, то тело будет двигаться по круговой орбите. Если скорость превышает круговую, то тело будет двигаться по эллипсу, причём перигей эллипса окажется в точке выхода на орбиту.
спутника очень мала по сравнению с массой Земли.
Круговая скорость спутника на расстоянии r = R + h:
vc= Ö(fm/(R+h)) = Ö(gR2/(R+h)),
где m - масса Земли, R- её радиус.
У воображаемого спутника, движущегося по окружности у самой поверхности Земли (h = 0), при R = 6.378.108см скорость должна быть равна
v1k= 7, 91 км/с.
Это первая космическая скорость относительно Земли.
Из-за наличия у Земли атмосферы, спутник, движущийся у самой поверхности, реально существовать не может. Поэтому запуск ИСЗ производится на некоторой высоте h>150 км.
Круговая скорость на высоте h меньше 1-й космической и определяется по формуле:
vc= v1k Ö(R/(R+h)).
Элементы орбиты ИСЗ зависят от места и времени его запуска, от величины и направления начальной скорости.
Связь между большой полуосью орбиты спутника а и его начальной скоростью определяется по формуле:
vo2= Gm(2/r0- 1/a),
где - r0расстояние точки выхода ИСЗ на орбиту от центра Земли.
Обычно запуск ИСЗ производится перпендикулярно к радиальному направлению.
Эллиптическая орбита ИСЗ. Эксцентриситет при горизонтальном запуске:
e = 1 - q/a.
где q - расстояние перигея (ближайшей точки орбиты от центра Земли).
Расстояние апогея Q = a(1 + e) = R + hA.
hA - высота апогея над земной поверхностью.
Период обращения спутника вычисляется по третьему закону Кеплера:
T = 2pa3/2/RÖg.
при R = 6370 км и g = 981 см/с2 - Т = 1,659.10-4а3/2 (мин)
Зависимость формы орбиты ИСЗ от начальной скорости, с которой он выведен на орбиту показана на рисунке. 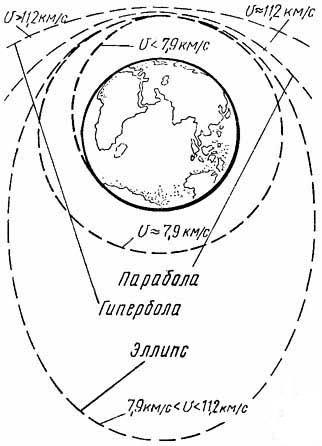
Если в точке К спутнику сообщена горизонтальная скорость, равная круговой для этого расстояния от центра Земли, то он будет двигаться по круговой орбите (1). Если начальная скорость в точке К меньше круговой, то спутник будет двигаться по эллипсу (2), а при очень малой скорости по эллипсу (3), сильно вытянутому и пересекающему поверхность Земли. Выпущенный спутник упадёт на поверхность Земли, не совершив и одного оборота. Если скорость в точке К больше соответствующей круговой, но меньше параболической, то спутник будет двигаться по эллипсу (4).
Основные причины, изменяющие эллиптическую орбиту спутника - экваториальное утолщение Земли и влияние сопротивления Земли.
Вторая причина вызывает изменение высоты спутника и изменение формы орбиты. Основное сопротивление и уменьшение скорости спутника происходит вблизи перигея. Высота апогея спутника с каждым оборотом заметно уменьшается. Уменьшается большая полуось и орбита округляется. Когда высота апогея становится сравнимой с высотой перигея, спутник испытывает торможение, теряет свою скорость вдоль всей орбиты. Спутник приближается по спирали к поверхности Земли, входит в плотные слои атмосферы и сгорает.
Траектория космического аппарата состоит из двух основных участков - активного и пассивного. Движение на активном участке определяется тягой реактивных двигателей и притяжением Земли. Пассивный участок начинается с момента выключения двигателя последней ступени. На пассивном участке космический аппарат движется под действие притяжения Земли и других тел Солнечной системы.
Для того, чтобы космический аппарат преодолел притяжение Земли и ушёл в космическое пространство, необходимо в начале пассивного участка сообщить ему скорость, равную или большую скорости
v = vcÖ2 =Ö(2Gm/(R+h)) ,
где h - высота начальной точки пассивного участка.
У поверхности Земли h = 0 и v2k = v1k Ö2 = 11,2 км/с.
Это вторая космическая скорость относительно Земли.
Скорость космического аппарата в любой точке на пассивном участке (без учёта возмущений) определяется по формуле:
v2 = Gm(2/r - 1/a).
Для того, чтобы космический аппарат, преодолев притяжение Земли и войдя в сферу действия Солнца, не упал на его поверхность, он должен иметь в этот момент скорость относительно Солнца, отличную от нуля.
Скорость, при которой запущенный с Земли космический аппарат может уйти за пределы Солнечной системы, сильно зависит от направления выхода аппарата из сферы действия Земли по отношению к направлению орбитального движения Земли и лежит в пределах 16,6 км/с <v0< 72,8 км/с.
Минимальная скорость v3k = 16,6 км/с называется третьей космической скоростью относительно Земли.
9.2 Проблема межзвёздных перелётов.
1. Межзвёздные перелёты имеют ряд существенных особенностей, сильно отличающих их от полётов в границах Солнечной системы. Межзвёздные перелёты возможны лишь при скорости сравнимой со скоростью света. Согласно теории относительности А. Эйнштейна, время, текущее в корабле, проходит с иной скоростью, чем для людей, оставшихся на Земле.
Для космонавтов имеется возможность перелететь огромные расстояния, равные сотням и тысячам световых лет, и остаться в живых.
Пусть летательный аппарат движется с постоянным ускорением а и на половине пути до цели полёта начнёт тормозить с тем же ускорением.
Американский астроном Карл Саган приводит формулы для времени полёта t, по часам космонавтов:
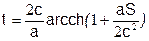 ,
,
где S - длина перелёта.
По вычислениям, при a = g космолёт долетит до ближайших звёзд за несколько лет, до ядра Галактики, удалённого на 30 000 св. лет - за 21 год, до Туманности Андромеды за 28 лет.
Пока корабль совершит свой перелёт в оба конца, на Земле пройдёт время равное удвоенному расстоянию до цели, выраженному в световых годах. До туманности Андромеды и обратно космонавты будут лететь по земным часам 3 млн. лет. До скопления галактик в Волосах Вероники - несколько сот миллионов лет.
Для межгалактических перелётов
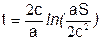 .
.
При S = 2 .1026см (расстояние до скопления в Com Ber) t = 38 лет.
Полёт с околосветовой скоростью сопряжён с огромными трудностями.
Ускорение и замедление ракеты требует огромных ресурсов энергии. Трудности, возникающие при этом, врядли преодолимы.
При приемлемом для нас соотношении начальной массы ракеты М0к массе, оставшейся после выгорания горючего М1, скорость ракеты после выгорания горючего V составит лишь малую часть скорости света. Это будет даже при использовании ядерных реакций в качестве источника энергии.
Из формулы теории реактивного движения следует:
V/W = ln (М1/М0),
где W - скорость выброса рабочего вещества ракеты.
Maксимально возможная величина W при урановой реакции будет около 13 000 км/с.
Значит для того, чтобы скорость ракеты после выгорания горючего V была порядка скорости света, надо чтобы М0было в сотни раз больше чем М1, что неприемлемо. Значит только фотонная ракета, для которой W = с, может обеспечить межзвёздный полёт со скоростью, близкой с.
При этом возникают новые трудности.
Из теории реактивного движения следует, что ускорение ракеты b определяется:
b = 2P/W,
где Р - отношение мощности двигателей ракеты к её полной массе.
В случае фотонной ракеты
b = P/c.
Если мы хотим, что бы b = g, нужно чтобы Р = 3 млн. Вт/гр. Это очень большая величина.
При мощности двигателя 15 млн. Вт (как у современной атомной подводной лодки) вес корабля должен был бы быть 5 граммов.
На современном уровне развития техники фотонные ракеты построить нельзя. Однако, в 19 столетии собирались лететь на Луну с помощью парового двигателя. Может в 21 веке откроются новые возможности. Реактивные двигатели для межзвёздных полётов непригодны.
Бюссар выдвинул предположение, что можно будет использовать межзвёздную среду для термоядерного горючего. Звездолёту не придётся нести с собой запасы топлива.
Межзвёздный газ состоит из атомов водорода. На ракете нужно поставить термоядерное устройство, синтезирующее из ядер водорода ядра дейтерия.
Особенностью этого летального аппарата является то, что поверхность всасывания межзвёздного газа должна быть очень большой. Если масса ракеты равна 100 т., то поверхность всасывания межзвёздного газа должна быть около 700 км.
Очень большой трудностью является возможность столкновения летательного аппарата, движущегося со световой скоростью, с атомами и пылинками межзвёздной среды.
При концентрации 1 атом на см3 поток энергии в форме космических лучей через переднюю поверхность ракеты будет 2.1011эрг/см2.
Экранирующие устройства вряд ли возможны.
Существует проект ионизации встречных атомов с помощью какого-то аппарата и отклонения их в сторону сильным магнитным полем.
2. Посещалась ли Земля инопланетянами в прошлом?
Анализируя многие легенды и мифы древности, можно предположить, что да. М.М. Агрест считает, что они могли оставить памятник о себе на обратной стороне Луны, что бы человечество его рассмотрело только достигнув высокого уровня развития.
К. Саган считает, что в Галактике одновременно существует около 106технически развитых цивилизаций. Время существования такой цивилизации может достигать 107лет. Если каждая цивилизация ежегодно посылает один корабль для исследования космоса, то средний интервал между посещениями какой-нибудь звезды будет 105лет.
Средний интервал между посещениями планеты с разумной жизнью будет меньше и составит несколько тысяч лет. Значит, на Земле могли быть такие посещения.
3. Можно не обязательно летать самим космонавтам и необязательно далеко. На расстоянии до ближайших инопланетных цивилизаций около 10 св. лет, подходят для жизни звёзды Эпс. Эридана, Тау Кита, Эпс. Индейца.
Если взять расстояние около 100 св. лет, то таких звёзд будет несколько тысяч. Для исследования ближайших планетных систем можно посылать автоматические зонды. Техника посадки зонда на круговую орбиту вокруг звезды уже разработана.
Высокоорганизованная цивилизация может посылать искусственные спутники ко многим ближайшим звёздам. Скорость движения может достигать 100 - 200 000 км/с. Эта скорость велика, но не сравнима со скоростью света, следовательно, не будет релятивистских эффектов.
Потребуется несколько столетий, чтобы вокруг всех звёзд на расстоянии 100 св. лет обращались искусственные спутники.
Дата добавления: 2014-12-17; просмотров: 2799;
