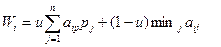Глава 1 Периодические дроби. 1. Складемо платіжну матрицю даної гри
1. Складемо платіжну матрицю даної гри. Її коефіцієнтами будуть значення прибутку від виробництва капусти, одержані як різниця суми виторгу від реалізації капусти й витрат на виробництво, зберігання й реалізацію капусти
| S1 | S2 | S3 | |
| A1 | |||
| A2 | |||
| A3 | -10 |
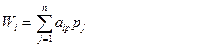 |
2. Визначимо найбільш вигідну стратегію за критерієм максимального математичного очікування виграшу (Байєса) по формулі :
W1 = 10×0,3 + 5×0,6 + 2×0,1 = 6,2
W2 = 0×0,3 + 10×0,6 + 3×0,1 = 6,3
W3 = -10×0,3 + 0×0,6 + 20×0,1 = -1
W = max Wi = W2
| S1 | S2 | S3 | Wi ММ | |
| Pj | 0,3 | 0,6 | 0,1 | |
| A1 | 6.2 | |||
| A2 | 6.3 | |||
| A3 | -10 | -1 |
Оптимальною за даним критерієм при зазначених значеннях імовірностей стану ринку капусти буде стратегія A2 (W = 6,3).
 |
3. Визначимо найбільш вигідну стратегію за критерієм недостатньої умови Лапласа (НУ):
W = max Wi
W1 = (10+5+2)\ 3= 5,67
W2 (0+10+3)\ 3= 4,33
W3 = (-10+0+20)\ 3= 3,33
| S1 | S2 | S3 | Wi (Лапласа) | |
| A1 | 5,67 | |||
| A2 | 4,33 | |||
| A3 | -10 | 3,33 |
Оптимальною є стратегія A1 (W = 5,67).
4. Визначимо найбільш вигідну стратегію за критерієм Вальда (максиміна):
Wi = minj aij
W = max Wi
Звідси,
W1 = min (10, 5, 2) = 2
W2 = min (0, 10, 3) = 0
W3 = min (-10, 0 20) =-10
| S1 | S2 | S3 | Wi (Вальда) | |
| A1 | ||||
| A2 | ||||
| A3 | -10 | -10 |
Оптимальною стратегією по критерію Вальда є стратегія A1 (W = 2).
5. Визначимо оптимальну стратегію за критерієм песимізму-оптимізму Гурвіца при коефіцієнті песимізму, рівному 0,3 :
Wi = C×minj aij + (1-C) ×maxj aij
W = max Wi
W1 = 0,3* 2 +0, 7* 10= 7,6
W2 = 0,3* 0 +0, 7* 10= 7
W3 = 0,3* (-10) +0, 7* 20= 11
| S1 | S2 | S3 | Wi (ПО) | |
| A1 | 7,6 | |||
| A2 | ||||
| A3 | -10 |
Оптимальною є стратегія A3 (W = 11).
6. Визначимо найбільш вигідну стратегію підприємства за критерієм Ходжа-Лемана (мал. 6. ).
| S1 | S2 | S3 | Wi | |||
| Pj | 0,3 | 0,6 | 0,1 | ||||
| A1 | 4,94 | ||||||
| A2 | 4,41 | ||||||
| A3 | -10 | -3,7 |
Оптимальною для господарства буде стратегія A1 (W = 4,94).
7. Визначимо найбільш вигідну стратегію за критерієм мінімаксного ризику. Для цього розрахуємо матрицю ризиків (мал. 5.).
rij = amax j – aij
Ri = maxj rij
W = min Ri
| S1 | S2 | S3 | Ri | |
| A1 | ||||
| A2 | ||||
| A3 |
Оптимальною стратегією за критерієм мінімаксного ризику є стратегія A2 (W = 17).
8. Проведемо економічну інтерпретацію результатів рішення задачі.
Якщо підприємство має інформацію про ймовірності стану ринку капусти й значення цих імовірностей відповідають вихідним даним задачі, найбільш вигідною стратегією є продаж частини капусти в осінні місяці й зберігання капусти, що залишилася, для реалізації протягом зимових місяців (прибуток 6,3 тис. ум.од ). Ця ж стратегія є найбільш ефективною, якщо інформація про ймовірності станів ринку капусти відсутній і підприємству необхідно мінімізувати ступінь можливого ризику втрати прибутку в процесі ухвалення рішення (значення можливого ризику складе 17 тис. ум.од.).
При відсутності інформації про стан ринку найбільш істотним для підприємства є не максимізація, а одержання її гарантованого обсягу, хоча б і мінімального, найбільш доцільним рішенням є реалізація всієї капусти в осінні місяці (прибуток - 2 тис. ум.од. Ця ж стратегія є найбільш вигідною, якщо підприємство має інформацію про ймовірності станів ринку, що відповідає вихідним даним, але ця інформація не цілком достовірна (у випадку, якщо інформація має вірогідність 0,7, прибуток становитиме 4,94 тис. ум.од.).
Якщо інформація про ймовірності станів ринку відсутня і ризик значних втрат не є для підприємства визначальним фактором при ухваленні рішення, або якщо є підстави для оптимістичної оцінки ситуації на ринку капусти, при якому підприємство має можливість дістати найбільший прибуток від виробництва капусти, йому варто зберегти вирощену продукцію й реалізувати її у весняні місяці (прибуток становитиме відповідно 5.7 і 11 тис. ум.од.).
Глава 1 Периодические дроби
1.1 Из истории возникновения десятичных дробей
Математика — одна из древнейших наук, и ее первые шаги связаны с первыми же шагами человеческого разума. Она возникла в трудовой деятельности людей. Развиваясь, математика все точнее и точнее решала те сложные задачи, которые ставила перед человеком сама жизнь. В трудное положение в 17 веке попала торговля, все производство, экономика стран. Для мореплавателей нужны были точные карты, для купцов быстрые и правильные расчеты без обмана, для строительства станков, кораблей, храмов и жилищ – выверенные до 1мм чертежи. Производство развивалось, а неумение быстро и с большей точностью производить расчеты буквально тормозило развитие науки и техники. Жизнь ставила перед учеными задачу упростить вычисления, увеличить их точность и скорость. Этим требованиям удовлетворяли десятичные дроби.
К десятичным дробям математики пришли в разные времена в Азии и в Европе. Зарождение и развитие десятичных дробей в некоторых странах Азии было тесно связано с метрологией (учением о мерах). Уже во II в. до н.э. там существовала десятичная система мер длины.В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи, цуни, доли, порядковые, шерстинки, тончайшие, паутинки.
Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзю-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.
Более полную и систематическую трактовку получают десятичные дроби в трудах среднеазиатского ученного ал-Каши в 20-х годах XV в. Среднеазиатский город Самарканд был в XV в. большим культурным центром. Там в знаменитой обсерватории, созданной видным астрономом Улугбеком, внуком Тамерлана, работал в 20-х годах XV в. крупный ученый того времени – Джемшид Гиясэддинал-Каши. Это он впервые изложил учение о десятичных дробях.В своей книге «Ключ арифметики», написанной в 1427 г., ал-Каши пишет: «Астрономы применяют дроби, последовательными знаменателями которых являются 60 и его последовательные степени. По аналогии мы ввели дроби, в которых последовательными знаменателями являются 10 и его последовательные степени». Он вводит специфическую для десятичных дробей запись: целая и дробная часть пишутся в одной строке. Для отделения первой части от дробной он не применяет запятую, а пишет целую часть черными чернилами, дробную же – красными или отделяет целую часть от дробной вертикальной чертой.
В 1579 году десятичные дроби применяются в «Математическом каноне» французского математика Франсуа Виета (1540–1603), опубликованном в Париже. В этом сочинении, представляющем собой собрание тригонометрических таблиц, Виет решительно выступил в пользу употребления, как он выражался, тысячных и тысяч, сотых и сотен, десятых и десятков и т.д. взамен шестидесятеричной системы целых и дробей. При записи десятичных дробей Виет не придерживался какого-либо одного обозначения. Нередко он пишет как числитель, так и знаменатель, иногда отделяет цифры целой части от дробной вертикальной чертой, или же цифры целой части изображает жирным шрифтом, или, наконец, цифры дробной части дает более мелким шрифтом и подчеркивает. Обозначение дроби 2,135436 2 1579 Ф. Виет Франция
Открытие десятичных дробей ал-Каши стало известно в Европе лишь спустя 300 лет после того, как эти дроби были в конце XVI в. заново открыты С. Стевиным. Фламандский инженер и ученый Симон Стевин (1548-1620), около 150 лет после ал-Каши, изложил учение о десятичных дробях в Европе.
Его и считают изобретателем десятичных дробей. Стевин, уроженец Брюгге, вначале был купцом, затем во время Нидерландской революции инженером в войсках возглавлявшего республику Морица Оранского. «Астрологам, земледельцам, мерильщикам объемов, проверщикам емкостей бочек, стереометрам вообще, монетным мастерам и всему купечеству — Симона Стевина привет», — так обращается к своим читателям изобретатель десятичных дробей в своей книге «Десятая»(1585). Эта маленькая работа (всего 7 страниц) содержала объяснение записи и правил действий с десятичными дробями. В книге он старается убедить людей пользоваться десятичными дробями, говоря, что при их использовании «изживаются трудности, распри, ошибки, потери и прочие случайности, обычные спутники расчетов». Он писал цифры дробного числа в одну строку с цифрами целого числа, при этом нумеруя их.
Запись десятинных дробей у Стевина была отлична от нашей. Стевин указывал на большое практическое значение десятичных дробей и настойчиво пропагандировал их. Он был первым ученым, потребовавшим введения десятичной системы мер и весов.
Запятая в записи дробей впервые встречается в 1592г., а в 1617г. шотландский математик Джон Непер предложил отделять десятичные знаки от целого числа либо запятой, либо точкой.
Современную запись десятичных дробей т.е. отделение целой части запятой, предложил Иоганн Кеплер (1571 — 1630 гг.). В странах где говорят по английский (Англия, США, Канада и др.), вместо запятой пишут точку. Обозначение дроби 2,135436 2,135436 2.135436 1571 — 1630 Кеплер Германия. В России первые систематические сведения о десятичных дробях встречаются в “Арифметике” Магницкого (1703г.) С начала XVII века начинается интенсивное проникновение десятичных дробей в науку и практику. Развитие техники, промышленности и торговли требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в сельском хозяйстве и промышленности десятичные дроби и их частный вид – проценты – применяются намного чаще, чем обыкновенные дроби.
В странах, где говорят по-английски (Англия, США, Канада и др.), и сейчас вместо запятой пишут точку, например: 2.3 и читают: два точка три.
В «Арифметика, сиречь наука числительная» (1703) первого русского педагога-математика Леонтия Филипповича Магницкого (1669-1739) десятичным дробям была отведена отдельная глава. «Вратами своей учености» М. В. Ломоносов назвал эту книгу. Выход в 1703 г. Книги Магницкого явился важным фактом в истории математического просвещения в России. В течение полустолетия книга была «вратами учености» для русского юношества, стремившегося к образованию. Магницкий выходец из народа, родился в 1669 г., умер в 1739 г. Настоящая его фамилия неизвестна. Петр I многократно беседовал с ним о математических науках и был так восхищен его глубокими знаниями, притягивающими к нему людей, что называл его магнитом и приказал писаться Магницким.
1.2 Периодические дроби
Не все обыкновенные дроби можно представить в виде конечной десятичной дроби.
Например, если делить 2 на 3, то сначала получим ноль целых, потом шесть десятых, а затем при делении всё время будет повторяться остаток 2, а в частном - цифра 6.
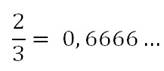
Такое деление закончить без остатка невозможно и поэтому дробь 2/3 нельзя представить в виде конечной десятичной дроби.
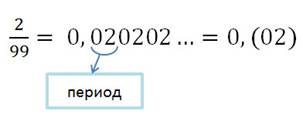
Если в записи десятичной дроби одна цифра или группа цифр начинают повторяться бесконечно много раз, такую дробь называют периодической дробью.
В краткой записи периодической дроби повторяющуюся цифру (или группу цифр) пишут в скобках. Эту цифру (или группу цифр) называют периодом дроби. Вместо 0,666... пишут 0,(6) и читают «ноль целых и шесть в периоде».
При решении примеров, содержащих десятичные дроби, часто приходится обращать их в обыкновенные. Обращение конечной дроби в обыкновенную не представляет особого труда: 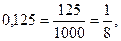
 .
.
Обращение бесконечной периодической дроби в обыкновенную требует определенных навыков. Обратим для примера дробь 0,(411):

В правой части равенства мы имеем сумму бесконечно убывающей геометрической прогрессии с 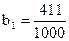 и
и 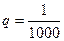 . Поэтому
. Поэтому
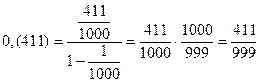 .
.
Таким образом, можно сформулировать правило обращения чисто периодической дроби:
Для обращения чисто периодической дроби 0,(a1 a2 a3 … aк) в обыкновенную 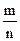 необходимо в числителе обыкновенной дроби записать группу цифр, образующих период десятичной дроби, а в знаменателе число из девяток, количество которых равно количеству цифр в периоде.
необходимо в числителе обыкновенной дроби записать группу цифр, образующих период десятичной дроби, а в знаменателе число из девяток, количество которых равно количеству цифр в периоде.
Дата добавления: 2014-11-30; просмотров: 1388;