ДИФРАКЦИОННОЙ РЕШЕТКИ

Приборы и принадлежности: дифракционный спектрометр

Цель работы: изучение спектров, получаемых с помощью дифракционной решетки (в качестве источника света используется лампа накаливания, дающая сплошной спектр);

определение длин волн для трех цветов видимой части спектра (красного, зеленого и фиолетового).

Краткие теоретические сведения:

Дифракцией светаназывается явление загибание волн в область геометрической тени.В оптике дифракция наблюдается, когда свет проходит через малое отверстие или встречает на своем пути небольшое количество препятствий.

Наличие дифракции хорошо объясняется принципом Гюйгенса Френеля, согласно которому каждая точка среды, до которой доходит фронт волны, является центром вторичных волн, поверхность, огибающая эти вторичные волны, представляет собой новый фронт распространяющейся волны. Все вторичные волны когерентны между собой и могут взаимодействовать (интерферировать) в любой точке,до которой онидоходят.

В результате интерференции в этой точке будет иметь место усиление или ослабление волн.

Рассмотрим прохождение плоской световой волны через узкую прямоугольную щель шириной АВ = а (рис. 1).

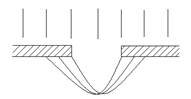
Рис. 1

Пусть щель освещается пучком параллельных лучей с длиной волны λ. Согласно принципа Гюйгенса, каждая точка фронта волны, достигающая щели, является источником вторичных волн, распространяющихся во все стороны. Поверхность, огибающие эти волны и представляющая фронт прошедшей через щель волны, заходит в область геометрической тени. Таким образом, при прохождении света через узкую щель имеет место явление дифракции.

Если за щелью поставить линзу L (рис. 2), то на экране в фокальной плоскости линзы будет наблюдаться следующая картина. В центре, в направлении падающих лучей будет видна яркая полоса, представляющая собой изображение щели, даваемой линзой по закону прямолинейного распространения света.

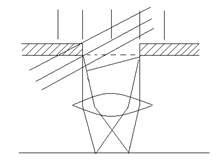
Рис.2

Но на экране кроме яркого центрального изображения щели наблюдается еще несколько изображений, значительно более слабых и не резко очерченных. Эти боковые изображения щели расположены симметрично по обеим сторонам центральной полосы и быстро убывает по яркости. Если на щель падает пучок монохроматических лучей, то на экране чередуются темные и светлые полосы, если же на щель падает пучок белого света, то боковые изображения будут спектрального о крашения.

Возникновения боковых изображений щели объясняется дифракционными явлениями. Для расчета дифракционной картины, получаемой за щелью, воспользуемся методом зон Френеля. Рассмотрим лучи распространяющиеся за щелью под некоторым углом j к первоначальному направлению (рис.2). Эти лучи соберутся в фокальной плоскости линзы в точке М. Для подсчета амплитуды колебаний в этой точке, рядом плоскостей, которые перпендикулярны прошедшим лучам и отстояли друг от друга на расстоянии λ/2, разделим фронт волны по ширине щели на зоны, называемые зонами Френеля. Эти волны представляют собой ряд узких полосок одинаковой ширины параллельных краям щели. Число Френеля, которое уложится на ширине щели:

Z = ;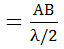

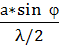Точки, одинаково расположенные по отношению к границам зон, называются соответственными. Разность хода волн, выходящих из соответственных точек соединяющих зон, равна λ/2. Поэтому колебания, приходящие в точку М от двух соседних зон, будут гасить друг друга, так как приходят в точку встречи в противоположных фазах.

В зависимости от величин угла j в щели может укладываться четное или нечетное число зон Френеля.

Если в щели укладывается четное число зон (Z = 2к, где к=1, 2, 3…), то действие каждой нечетной зоны подавляется (гасится) действием соседней четной зоны. Следовательно, в данном направлении свет распространятся не будет, в точке М на экране получится темная полоса (минимум света).

Если в щели укладывается нечетное число зон ( Z = 2к+1), то для одной зоны не окажется парной, свет идущий от нее, не будет погашен и в точке М будет наблюдаться светлая полоса (максимум света).

Итак, темные полосы будут наблюдаться при условии (условие минимума света)

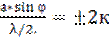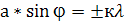или ; (1)

Светлые полосы будут наблюдаться при условии (условие максимума света)

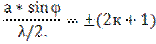
или 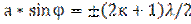; (2)

где к = 1, 2, 3… и называется порядком максимума.

В направлении φ=0 наблюдается самая яркая полоса (центральный максимум нулевого порядка); в этом направлении колебания от всех зон проходят одинаковые оптические пути и приходят в точку 0 в одинаковых фазах. Затем, при постепенном изменении угла 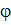, т.е. при перемещении по экрану, по обе стороны от центральной полосы будут наблюдаться чередующиеся темные и светлые полосы. В направлениях, определяемых условием (2), будут наблюдаться светлые полосы: при к=1 максимум первого порядка, при к=2 – максимумы второго порядка и т.д.

Знак «+» или «-» соответствует расположению полос справа или слева от центрального максимума нулевого порядка.

Распределение интенсивности света J в зависимости от угла 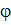дано на рис. 3 (А-амплитуда колебания, в – коэффициент упругости).

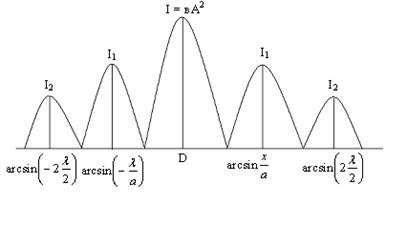
Рис.3